单振幅量子虚拟机

背景与方案细节

短期内，量子霸权的存在，超出了现有经典算法在最先进计算机或超算上的能力，这刺激了最近在模拟量子电路的经典算法方面的进展。

与适用于低比特高深度的全向量模拟相比，单振幅模拟器将量子电路的模拟推广到一个无向图形模型上，并在精确推理的背景下，利用变量消去算法进行了计算。

首先我们在量子线路演化中引入费曼路径积分方法。

我们用酉矩阵的乘积来表示量子电路 \(U^{(t)}\) ，其中t表示不同的时钟周期。

在电路的最后一个周期后，我们引入以下符号来表示特定量子位串的振幅。

\[\langle x|\mathcal{U}| 0 \ldots 0\rangle=\sum_{\left\{b^t\right\}} \prod_{t=0}^{d-1}\left\langle b^{t+1}\left|U^{(t)}\right| b^t\right\rangle, \quad\left|b^d\right\rangle=|x\rangle\]

这里 \(\left|b^t\right\rangle=\otimes_{j=1}^n\left|b_j^t\right\rangle\) ，以及 \(\left|b_i^t\right\rangle\) 对应量子态 \(|0\rangle\) 或 \(|1\rangle\) 的第 \(j\)-th 比特。

上述表达式可以看作是n量子位系统的 \(\left\{b^0, \ldots, b^d\right\}\) 的费曼路径积分形式。

根据上文所说，一个量子线路是多个酉矩阵的乘积，即 \(\mathcal{U}=U_g \cdots U_1\) ，其中对于一个对角矩阵可以用如下表述：

\[U=\sum_{b \in\{0,1\}} \psi_U(b)|b\rangle\langle b| \quad \text { (diagonal) }\]

其中 \(\psi_U(b)\) 是一个布尔变量的复函数，对于一个非对角矩阵，比如 \(\mathrm{H}, \mathrm{X}^{1 / 2}, \mathrm{Y}^{1 / 2}\) ,有

\[U=\sum_{b, b^{\prime} \in\{0,1\}} \psi_U\left(b^{\prime}, b\right)\left|b^{\prime}\right\rangle\langle b| \quad \text { (non-diagonal) }\]

其中 \(\psi_U\left(b, b^{\prime}\right)\) 是两个布尔变量的复函数，例如对于一个H门， \(\psi_{\mathrm{H}}(1,1)= -1 / \sqrt{2}\) , 其他项等于 \(1 / \sqrt{2}\) 。 一个对角双门，例如CZ，可以写成如下形式

\[U=\mathrm{CZ}=\sum_{b, b^{\prime} \in\{0,1\}} \psi_{\mathrm{CZ}}\left(b, b^{\prime}\right)\left|b, b^{\prime}\right\rangle\left\langle b, b^{\prime}\right|,\]

根据对角矩阵和非对角矩阵的性质，可以在有向无环图中分别用不同形状表示，以如下量子线路为例

../_images/single1.png

假设以初态 \(| 00\rangle\) 计算量子态末态为 \(| 00\rangle\) 的概率，对应的有向无环图模型为

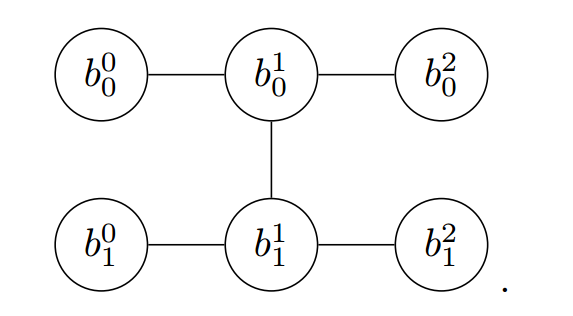
../_images/single2.png

因为初态和末态是确定的，我们有 \(b_0^0=b_0^2=b_1^0=b_1^2=0\) 。图可以简化为如下形式：

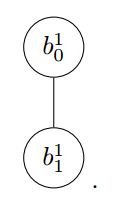
../_images/single3.png

这个图的树宽为2 ,我们可以计算出

\[\begin{split}\begin{array}{r} \langle 00|C| 00\rangle=\sum_{b_0^1, b_1^1} \psi_{\mathrm{H}}\left(0, b_0^1\right) \psi_{\mathrm{CZ}}\left(b_0^1, b_1^1\right) \psi_{\mathrm{H}}\left(b_0^1, 0\right) \\ \psi_{\mathrm{H}}\left(0, b_1^1\right) \psi_{\mathrm{H}}\left(b_1^1, 0\right) . \end{array}\end{split}\]

函数 \(\psi_{\mathrm{H}}\) 对应的H门映射表可以写为

\[\begin{split}\begin{array}{|ll|c|} \hline 0 & 0 & 1 / \sqrt{2} \\ 0 & 1 & 1 / \sqrt{2} \\ 1 & 0 & 1 / \sqrt{2} \\ 1 & 1 & -1 / \sqrt{2} \\ \hline \end{array}\end{split}\]

函数 \(\psi_{\mathrm{CZ}}\) 对应的CZ门映射表可以写为

\[\begin{split}\begin{array}{|ll|c|} \hline 0 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & -1 \\ \hline \end{array}\end{split}\]

上面的等式就可以重写为

\[\langle 00|C| 00\rangle=\sum_{b_0^1, b_1^1} \tau_1\left(b_0^1, b_1^1\right)\]

其中表中 \(\tau_1\) 的映射关系为

\[\begin{split}\begin{array}{|ll|c|} \hline 0 & 0 & 1 / 4 \\ 0 & 1 & 1 / 4 \\ 1 & 0 & 1 / 4 \\ 1 & 1 & -1 / 4 \\ \hline \end{array}\end{split}\]

如果我们把所有的 \(b_1^1\) 相加可以得到

\[\langle 00|C| 00\rangle=\sum_{b_0^1} \tau_2\left(b_0^1\right)\]

其中 \(\tau_2\) 为

\[\begin{split}\begin{array}{|c|c|} \hline 0 & 1 / 2 \\ 1 & 0 \\ \hline \end{array}\end{split}\]

最终， 对 \(b_0^1\) 求和，可以计算出末态的概率

\[\langle 00|C| 00\rangle=1 / 2 .\]

使用介绍

class SingleAmpQVM(QuantumMachine)

量子单振幅模拟器类

该类实现了基于单振幅的量子线路模拟，借助于费曼积分路径和quickBB，可以快速模拟大比特稀疏量子线路的单个振幅

__init__()

初始化单振幅模拟器类实例。

pmeasure_bin_amplitude(bin_string: str) → complex

获取指定二进制字符串的量子态振幅。

参数:

bin_string (str) -- 二进制字符串。

返回:

指定二进制字符串的量子态振幅。

返回类型:

complex

抛出:

run_fail -- 获取振幅失败。

pmeasure_bin_index(bin_string: str) → float

获取指定二进制字符串的量子态概率振幅。

参数:

bin_string (str) -- 二进制字符串。

返回:

指定二进制字符串的量子态概率振幅。

返回类型:

float

抛出:

run_fail -- 获取概率振幅失败。

pmeasure_dec_amplitude(dec_string: str) → complex

获取指定十进制字符串的量子态振幅。

参数:

dec_string (str) -- 十进制字符串。

返回:

指定十进制字符串的量子态振幅。

返回类型:

complex

抛出:

run_fail -- 获取振幅失败。

pmeasure_dec_index(dec_string: str) → float

获取指定十进制字符串的量子态概率振幅。

参数:

dec_string (str) -- 十进制字符串。

返回:

指定十进制字符串的量子态概率振幅。

返回类型:

float

抛出:

run_fail -- 获取概率振幅失败。

run(prog: QProg, qubit_list: QVec, max_rank: int = 30, alloted_time: int = 5) → None

运行量子程序。

参数:

  • prog (QProg) -- 要运行的量子程序。

  • qubit_list (QVec) -- 用于运行的量子比特列表。

  • max_rank (int, optional) -- 最大秩限制。默认为 30。

  • alloted_time (int, optional) -- 允许quickBB的运行时间。默认为 5。

返回:

无返回

其使用方式与前面介绍的量子虚拟机模块非常类似，首先通过 SingleAmpQVM 初始化一个单振幅量子虚拟机对象用于管理后续一系列行为。

from pyqpanda import *
from numpy import pi

qvm = SingleAmpQVM()

然后是量子程序的初始化、构建与装载过程：

qvm.init_qvm()

qv = qvm.qAlloc_many(10)
cv = qvm.cAlloc_many(10)

prog = QProg()

# 构建量子程序
prog << CZ(qv[1], qv[5])\
    << CZ(qv[3], qv[5])\
    << CZ(qv[2], qv[4])\
    << CZ(qv[3], qv[7])\
    << CZ(qv[0], qv[4])\
    << RY(qv[7], pi / 2)\
    << RX(qv[8], pi / 2)\
    << RX(qv[9], pi / 2)\
    << CR(qv[0], qv[1], pi)\
    << CR(qv[2], qv[3], pi)\
    << RY(qv[4], pi / 2)\
    << RZ(qv[5], pi / 4)\
    << RX(qv[6], pi / 2)\
    << RZ(qv[7], pi / 4)\
    << CR(qv[8], qv[9], pi)\
    << CR(qv[1], qv[2], pi)\
    << RY(qv[3], pi / 2)\
    << RX(qv[4], pi / 2)\
    << RX(qv[5], pi / 2)\
    << CR(qv[9], qv[1], pi)\
    << RY(qv[1], pi / 2)\
    << RY(qv[2], pi / 2)\
    << RZ(qv[3], pi / 4)\
    << CR(qv[7], qv[8], pi)

然后是调用计算接口，需要注意的是， run 方法是调用计算振幅前必须调用的函数，用于正确生成有向无环图和计算路径，

pmeasure_bin_index ,使用时需要结合 run 方法。用法示例：

# run 有三个参数，默认2个，
# 第一个执行的量子程序
# 第二个为申请的量子比特
# 第三个为最大RANK，这里根据内存设置，默认30
# 第四个就是quickBB优化的最大运行时间，默认5s

qvm.run(prog, qv)
bin_result = qvm.pmeasure_bin_index("0001000000")
print("0001000000 : ", bin_result)

结果输出如下：

0001000000 :  0.001953123603016138

pmeasure_dec_index ,使用时需要结合 run 方法。用法示例：

qvm.run(prog, qv)
dec_result = qvm.pmeasure_dec_index("2")
print("2 : ",dec_result)

结果输出如下：

2 :  0.001953123603016138