量子计算背景

什么是量子计算

量子计算是一种遵循量子力学规律调控量子信息单元进行计算的新型计算模式，在理解量子计算的概念时，通常将它和经典计算相比较。

如图，经典计算使用2进制的数字电子方式进行运算，而二进制总是处于0或1的确定状态。

量子计算和现有的计算模式完全不同，它借助量子力学的叠加特性，能够实现计算状态的叠加，它不仅包含0和1，还包含0和1同时存在的叠加态。

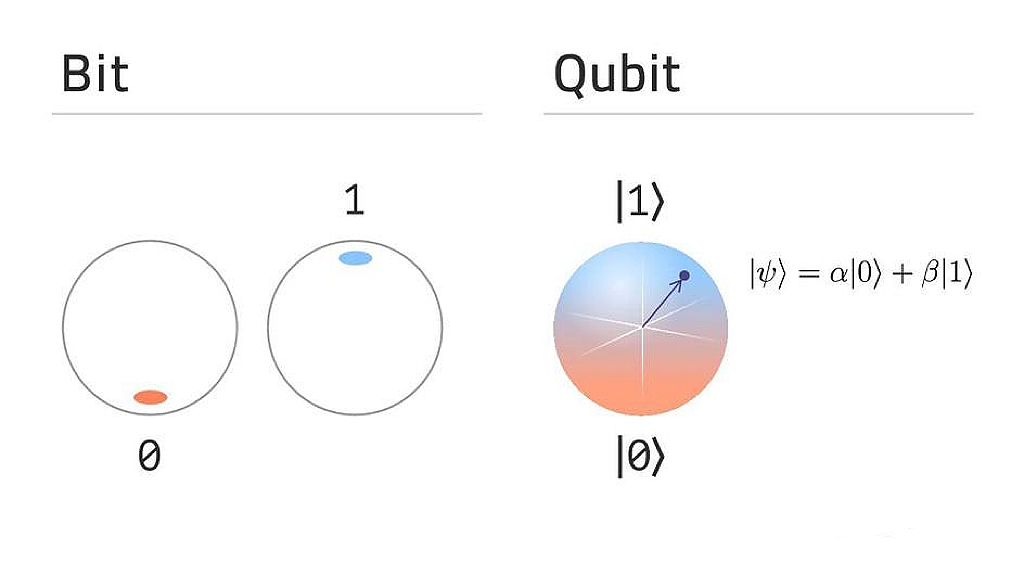
../_images/1.1.png

普通计算机中的2位寄存器在某一时间仅能存储4个二进制数（00、01、10、11）中的一个，而量子计算机中的2位量子位寄存器可同时存储这四种状态的叠加状态。

随着量子比特数目的递增，对于n个量子比特而言，量子信息可以处于2种可能状态的叠加，配合量子力学演化的并行性，可以展现比传统计算机更快的处理速度。

加上量子纠缠等特性，理论上，量子计算机相较于当前使用最强算法的经典计算机，在一些具体问题上，有更快的处理速度和更强的处理能力。

量子计算的发展

早在 1981 年，物理学家理查德·费曼（Richard Feynman）就提出了量子计算机的概念，他设想如果拓展一下计算机的工作方式，不使用逻辑门来建造计算机，而是一些其他的东西，比如分子和原子。 如果使用这些量子材料，它们具有非常奇异的性质，尤其是波粒二象性，是否能建造出模拟量子系统的计算机？于是他提出了这个问题并做了一些验证性实验，然后他推测，这个想法也许可以实现。由此，基于量子力学的新型计算机的研究被提上了科学发展的历程。

此后，计算机科学家们一直在努力攻克这一艰巨挑战。伴随时代发展的趋势，在20世纪90年代，量子计算机的算法发展得到了巨大的进步。

1992年Deutsch和Jozsa提出了D-J量子算法，开启了如今量子计算飞速发展的大幕。

1994年Peter Shor提出了Shor算法，这一算法在大数分解方面比目前已知的最有效的经典质因数分解算法快得多，因此对RSA加密极具威胁性，该算法带来巨大影响力的同时也进一步坚定了科学家们发展量子计算机的决心。

1996年Lov Grover提出了Grover量子搜索算法，该算法被公认为继Shor算法后的第二大算法。

2009年MIT三位科学家联合开发了一种求解线性系统的HHL量子算法。众所周知，线性系统是很多科学家和工程领域的核心，由于HHL算法在特定条件下实现了相较于经典算法有指数加速效果，这是未来能够在机器学习，人工智能科技得以突破的关键性技术。

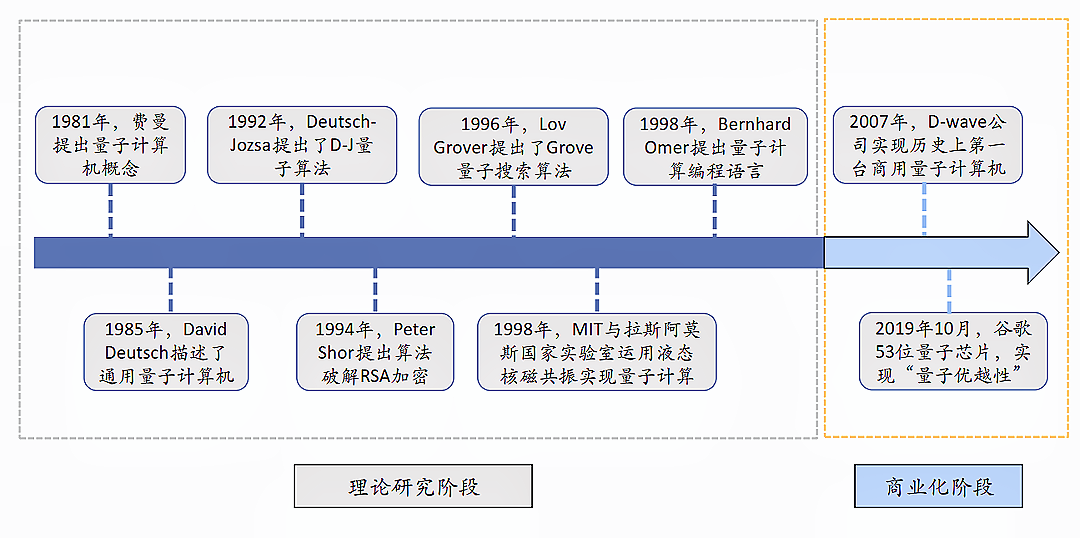
../_images/history.png

随着上述量子计算理论的探索，硬件也在飞速发展，2013年加拿大D-Wave系统公司发布了512比特的量子计算设备。

2016年，IBM发布了6量子比特的可编程量子计算机。

2017年本源量子发布了32位量子计算虚拟系统，同时还建立了以32位量子计算虚拟系统为基础的本源量子计算云平台。

2018年初Intel和Google分别测试了49位和72位量子芯片。

2018年12月6日，本源量子发布了第一款测控一体机Origin Quantum AIO，不仅提高了综合量子测控能力，更节约了量子测控环节各种大型设备的空间，为量子计算行业的高精尖仪器带来了更多的可能。

2019年1月，IBM发布了世界上第一台独立的量子计算机IBM Q System One。

2020年9月12日，本源量子完全自主开发的超导量子计算云平台正式向全球用户开放，该平台基于本源量子自主研发的超导量子计算机——本源悟源（搭载6比特超导量子处理器夸父 KF C6-130）。

量子计算机的发展目标

根据量子计算机的发展趋势，目前量子计算机的发展可以大致分为 3 个阶段：

第一阶段：能够对大约 50 个量子比特进行有效操纵，并且在实验上可以在特定问题的求解上展现出“量子优越性”，这一阶段目前已经实现；

第二阶段：由于量子计算机在运算过程中极易受到外界的干扰，因此需要大量冗余的量子比特来实现运算中的量子纠错，人们预计需要对几百个量子比特进行有效操纵，从而实现量子纠错的关键技术，并且进一步探索量子计算的实际应用场景；

第三阶段：需要对大约 10~100 万量级的量子比特进行有效操纵，从而构建可编程的通用量子计算机，并且最终实现加密密钥破解以及最佳优化搜索等。

9月10日，在国内量子计算领域占据重要一席的本源量子发布未来五年量子计算技术规划路线图。

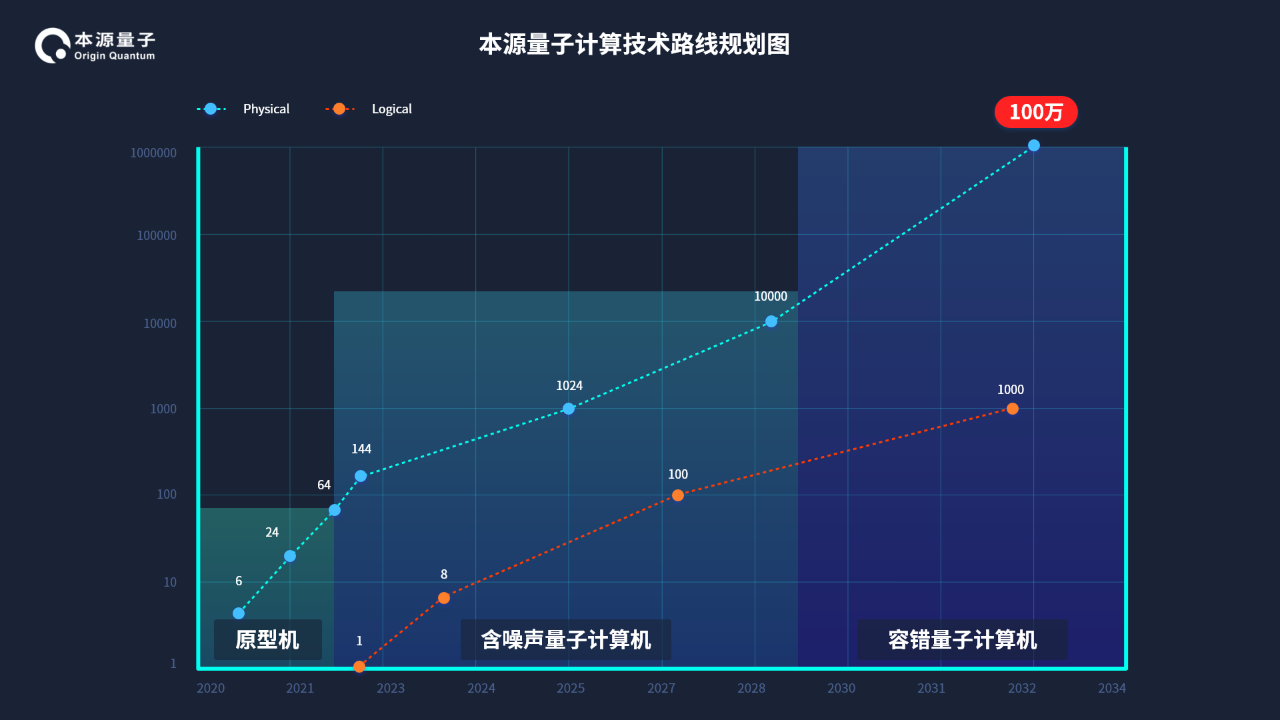
../_images/develop.png

路线图显示，到2025年，本源量子将突破1000位量子比特，达到1024位量子比特，这将意味着专用量子计算机的形成，并将实际运用到一些行业领域中。

量子计算理论基础

对于一个非物理专业的人而言，量子力学概念晦涩难懂。鉴于此，本章节仅介绍量子力学的一些基础概念加之部分数学的相关知识，甚至不涉及薛定谔方程，就足够开始量子计算机的应用。 这如同不需去了解CPU的工作原理以及经典计算机的组成原理，但仍能在日常生活中使用经典计算机或者编写经典程序一样。

量子态

量子（quantum）是现代物理学的重要概念。即一个物理量如果存在最小的不可分割的基本单位，此最小单位称为量子. 量子具有四个基本特性，了解其特性也有助于我们更好地理解量子的本质。

量子具有如下特性:

  • 量子化：描述物体长度时，一定会遇到最小的不可分割的基本单位，这一现象也称为量子化

  • 跃迁：当一个原子中的电子获得来自原子外的能量时，它就有可能克服能级之间的能量差距，跳到另外一个态上面

  • 量子叠加态：对于量子本身，它能同时存在于很多状态的叠加上

  • 测量和坍塌：测量会影响这个粒子本身的状态

量子态是一个微观粒子的状态。可用线性代数中的向量来描述量子态，在量子理论 中，描述量子态的向量称为态矢，态矢分为左矢和右矢。

\[\begin{split}\begin{aligned} \text{ket} & |\psi\rangle =[c_{1},c_{2},\cdots, c_{n}]^{T}\\ \text{bra} & \langle\psi| =[c_{1}^{*},c_{2}^{*},\cdots, c_{n}^{*}] \end{aligned}\end{split}\]

相应地，内积与外积定义为：设 \(|\alpha\rangle=[a_{1},a_{2},\cdots, a_{n}]^{T}\) ， \(|\beta\rangle=[b_{1},b_{2},\cdots, b_{n}]^{T}\) ，

\[\begin{split}\begin{aligned} \text{} & \langle\alpha \vert\beta\rangle =\sum_{i=1}^{n}a_{i}b_{i}\\ \text{} & |\alpha\rangle \langle\beta| =\left[a_{i}b_{j}^{*}\right]_{n\times n} \end{aligned}\end{split}\]

量子比特

量子比特是量子计算中的基本单元. 一个量子比特（qubit）就是二维复向量空间 \(\mathbb{C}^{2}\) 中一个单位向量.设 \(|0\rangle=[1,0]^{T}\) , \(|1\rangle=[0,1]^{T}\) 为 \(\mathbb{C}^{2}\) 的一组基，则一个量子比特可以表示为

\[\begin{aligned}\label{equ:Psi} |\psi\rangle=\alpha|0\rangle+\beta|1\rangle, \end{aligned}\]

其中，\(\alpha,\beta\in\mathbb{C}\) 且 \((\alpha,\beta)\ne (0,0)\) ， \(\vert\alpha\vert^2+\vert\beta\vert^2=1\) ， \(\alpha,\beta\) 称为振幅。 并且 \(\vert\alpha\vert^2+\vert\beta\vert^2=1\) 。

纯态和混合态

我们看到的具有精确已知状态的量子系统均是纯态（pure state）。 所以纯态 \(|\psi\rangle\) 可以用向量表示，且其密度矩阵表示为 \(\rho=|\psi\rangle\langle\psi|\) ，以100%的概率处在状态 \(|\psi\rangle\) 。

如果系统并非处于一个态中，而是以 \(p_{i}\) 的概率处于 \(|\psi_{i}\rangle(i=1,\cdots,n)\) ，这种状态无法用一个态矢量来描述，称之为混合态。其密度矩阵表示为：

\[\begin{aligned} \rho_{mix}=\sum_{i} p_{i}|\psi_{i}\rangle\langle\psi_{i}|. \end{aligned}\]

综上所述，对于纯态它可以借助向量和密度矩阵两种形式进行描述。但是对于混合态，只能借助密度矩阵的形式进行描述。易知混合态不是叠加态，叠加态不是混合态；纯态可以是本征态，也可以是叠加态。

纯态具有如下性质：

  • 1.密度矩阵 \(\rho\) 是幂等的，即 \(\rho^{2}=|\psi\rangle\langle\psi|\psi\rangle\langle\psi|=\rho\)

  • 2.在任意正交基下的 \(\rho\) 的迹 \(tr(\rho)=\sum_{i}\langle i|\rho|i\rangle=\sum_{i}\langle i|\psi\rangle\langle\psi|i\rangle=\langle\psi|\psi\rangle=1\) ，进而 \(tr(\rho^{2})=1\)

  • 3.厄米特性：\(\rho^{\dagger}=\rho\)

  • 4.半正定性：\(\langle\phi|\rho|\phi\rangle=\langle\phi|\psi\rangle\langle\phi|\psi\rangle=|\langle\phi|\psi\rangle|^2\ge 0\)

混合态具有如下性质：

  • 1.密度矩阵 \(\rho_{mix}\) 是非幂等的，即 \(\rho_{mix}^{2}\ne\rho_{mix}\)

  • 2.在任意正交基下的 \(\rho_{mix}\) 的迹 \(tr(\rho_{mix})=1\) （所有可能的测量结果的相加）

  • 3.满足 \(tr(\rho_{mix}^{2})< 1\) (证明过程中用Schwartz不等式即可证得)

  • 4.厄米特性与半正定性

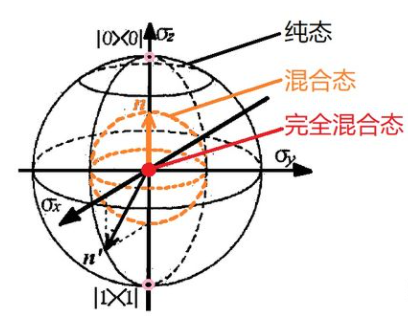
通过布洛赫球，可以更直观地理解纯态与混合态。球面上每一个点都能映射到一个纯态, 球内每一个点都能映射到混合态，完全混合 态（也称为最大混合态）是球心，它意味着这里不存在任何量子叠加性，具体可见下图

../_images/pure_state.png

酉变换

酉变换是一种矩阵，也是一种操作，它作用在量子态上得到的是一个新的量子态。使用 \(U\) 来表达酉矩阵, \(U^{\dagger}\) 表示酉矩阵的转置复共轭矩阵，二者满足运算关系 \(UU^{\dagger}=I\) ，所以酉矩阵的转置复共轭矩阵也是一个酉矩阵，说明酉变换是一种可逆变换。

一般酉变换在量子态上的作用是变换矩阵左乘以右矢进行计算的。例如一开始有一个量子态 \(|\psi_{0}\rangle\) , 经过酉变换 \(U\) 之后得到 \(|\psi\rangle=U\left|\psi_{0}\right\rangle\)

或者也可以写为

\[\langle\psi|=\left\langle\psi_{0}\right| U^{\dagger}\]

由此可见，两个矢量的内积经过同一个酉变换之后保持不变。

\[\langle\varphi \mid \psi\rangle=\langle\varphi|U^{\dagger}U| \psi\rangle\]

类似地，也可以通过酉变换表示密度矩阵的演化；

\[\rho=U{\rho_{0}} U^{\dagger}\]

这样就连混合态的演化也包含在内了。

量子态的测量

对量子态进行测量会导致坍塌，即测量会影响到原来的量子态，因此量子态的全部信息不可能通过一次测量得到.

下面，我们给出测量的通用计算表达式。

假设：量子测量是由测量算子（measurement operators）的集合 \(\{M_{i}\}\) 来描述，这些算子可以作用在待测量系统的状态空间（state space）上。 指标i表示在实验上可能发生的结果. 如果测量前的量子系统处在最新状态 \(|\psi\rangle\) ，那么测量结果i发生的概率为

\[\begin{aligned} p(i)=\langle \psi|M_{i}^{\dagger}M_{i}|\psi\rangle \end{aligned}\]

并且测量后的系统状态转变为

\[\begin{aligned} \dfrac{M_{i}|\psi\rangle}{\sqrt{\langle\psi|M_{i}^{\dagger}M_{i}|\psi}\rangle} \end{aligned}\]

由于所有可能情况的概率和为1，即

\[\begin{aligned} \sum_{i}p(i)=\sum_{i}\langle \psi|M_{i}^{\dagger}M_{i}|\psi\rangle=1 \end{aligned}\]

则测量算子需满足

\(\sum_{i}M_{i}^{\dagger}M_{i}=I\) 。该方程被称为完备性方程(completeness equation).

量子测量有多种方式，如投影测量（projective measurements）、正算子值测量 （Positive Operator-Valued Measure）. 投影测量要求测量算子为投影算子 \(\{P_{i}\}\) ，且满足 \(P_{i}^{\dagger}P_{i}=P_{i}^{2}=P_{i}\) 。 正算子值测量并非全新的概念，对于任意的测量算子 \(\{M_{i}\}\) ，我们记 \(E_{i}=M_{i}^{\dagger}M_{i}\) ，可以看出E是正定的，且是完备的( \(\sum_{i}E_{i}=I\) )，然后我们把 \(\{E_{i}\}\) 叫做正算子值测量. 可以说，投影测量与正算子值测量是一般测量的特例. 当测量算子具有酉矩阵时，投影测量和一般测量等价. 当测量算子是酉矩阵时，投影测量和一般测量等价.

这里介绍一下投影测量. 投影测量由一个可观测量（observable） \(\Lambda\) 来描述，可观测量是一个待观测系统 的状态空间上的自伴算子. 对可观测量 \(\Lambda\) 作谱分解

\[\begin{aligned} \Lambda=\sum_{i}\lambda_{i}P_{i} \end{aligned}\]

这里 \(\Lambda_{i}\) 是 \(\Lambda\) 在特征值 \(\lambda_{i}\) 对应的特征空间上的投影. 在对状态 \(|\psi\rangle\) 测量之后，得到结果i的概率为

\[\begin{aligned} p(i)=p(\lambda=\lambda_{i})=\langle\psi|P_{i}|\psi\rangle \end{aligned}\]

若测量后，结果i发生，则量子系统最新的状态为

\[\begin{aligned} \dfrac{\Lambda_{i}|\psi\rangle}{\sqrt{p_{i}}} \end{aligned}\]

投影测量有一个重要的特征就是很容易计算投影测量的平均值以及标准差：

\[E(\Lambda)=\sum_{i}\lambda_{i}p_{i}= \sum_{i}\lambda_{i}\langle\psi|P_{i}|\psi\rangle=\langle\psi|\Lambda|\psi\rangle\]
\[\Delta(\Lambda)^{2}= E(\Lambda^{2})- E(\Lambda)^{2}=\langle\psi|\Lambda^{2}|\psi\rangle-\langle\psi|\Lambda|\psi\rangle^{2}\]

若对量子态 \(|\psi\rangle\) 进行测量，测量结果为0的概率为

\[p(0)=\langle\psi|M_{0}^{\dagger}M_{0}|\psi\rangle=\langle\psi|M_{0}|\psi\rangle=\vert \alpha \vert^{2}\]

对应测量后的状态为

\[\dfrac{M_{0}|\psi\rangle}{\sqrt{\langle\psi|M_{0}^{\dagger}M_{0}|\psi}\rangle}=\dfrac{M_{0}|\psi\rangle}{|\alpha|}=\dfrac{\alpha}{|\alpha|}|0\rangle\]

同理可得到以概率 \(\vert \beta \vert^2\) 处于 \(|1\rangle\) ，对应测量后的状态为 \(\frac{\beta}{|\beta|}|1\rangle\) 。

对于投影测量，若可观测量是 \(X=\begin{bmatrix}0 & 1\\ 1 & 0 \end{bmatrix}\) ，现对待观测量 \(|\psi\rangle=\alpha|0\rangle+\beta|1\rangle\) 进行投影测量。

对X作谱分解得到 \(\Lambda=\lambda_{1}P_{1}+\lambda_{2}P_{2}\) ，其中 \(\lambda_{1}=1,\lambda_{2}=-1\) 以及投影算子 \(P_{1}=\begin{bmatrix} \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{bmatrix},P_{2}=\begin{bmatrix} \frac{1}{2} & -\frac{1}{2}\\ -\frac{1}{2} & \frac{1}{2} \end{bmatrix}\) 。

在对状态 \(|\psi\rangle\) 测量，可得到概率为 \(p(1)=p(\lambda=\lambda_{1})=\langle\psi|P_{1}|\psi\rangle=\frac{1}{2}(\alpha+\beta)^{2}\) 以及 \(p(2)=p(\lambda=\lambda_{2})=\langle\psi|P_{2}|\psi\rangle=\frac{1}{2}(\alpha-\beta)^{2}\) 。

若测量后，结果1发生，则量子系统最新的状态为

\[\begin{aligned} \dfrac{P_{1}|\psi\rangle}{\sqrt{p_{1}}}=\frac{\sqrt{2}}{2}(|0\rangle+|1\rangle)=|+\rangle \end{aligned}\]

结果2发生，则量子系统最新的状态为

\[\begin{aligned} \dfrac{P_{2}|\psi\rangle}{\sqrt{p_{2}}}=\frac{\sqrt{2}}{2}(|0\rangle-|1\rangle)=|-\rangle \end{aligned}\]

量子计算机

目前主流的量子计算芯片技术研发路线有超导量子计算机和半导体量子计算机两种。

超导量子芯片

超导量子计算是基于超导电路的量子计算方案，其核心器件是超导约瑟夫森结。超导量子电路在设计、制备和测量等方面，与现有的集成电路技术具有较高的兼容性，对量子比特的能级与耦合可以实现非常灵活的设计与控制，极具规模化的潜力。

由于近年来的迅速发展，超导量子计算已成为目前最有希望实现通用量子计算的候选方案之一。超导量子计算实验点致力于构建一个多比特超导量子计算架构平台，解决超导量子计算规模化量产中遇到的难题。

超导电路类似于传统的电子谐振电路，这种谐振电路产生了谐振子的能级。超导约瑟夫森效应使得超导电路在不发生损耗和退相干的情况下产生非线性，非线性导致谐振子的能级间隔不再等同，其中最低的两个能级可以用来实现量子比特的操控。

超导量子计算的研究始于2000年前后，后来在美国耶鲁大学Schoelkopf和Devoret研究组的推动下，将超导比特和微波腔进行耦合，实现了量子比特高保真度的读出和纠缠，加速了超导量子比特的研究。微波腔是一种容纳微波光子的谐振腔，比特的两个能级会对微波腔的光子产生扰动，这一信号的扰动就可以用来实现比特信号的读出。比特和比特之间还可以通过微波腔相连，当两个比特和腔是强耦合状态的时候，两个比特就会通过腔发生相互作用，物理学家通过这一相互作用实现了两比特操作。在2009年，基于超导比特和腔的耦合，实现了两比特的高保真度量子算法，使得超导量子计算得到了世界的广泛关注。

从2014年开始，美国企业界开始关注超导量子比特的研究，并加入了研究的大潮中。2014年9月，美国Google公司与美国加州大学圣芭芭拉分校合作研究超导量子比特，使用X-mon形式的超导量子比特

2017年，Google发布了实现量子计算机对经典计算机的超越——“量子霸权”的发展蓝图。2018年年初，其设计了72比特的量子芯片，并着手进行制备和测量，这是向实现量子霸权迈出的第一步。在Google公司加入量子计算大战的同时，美国国际商用机器有限公司（IBM）于2016年5月在云平台上发布了他们的五比特量子芯片。

2017年，IBM制备了20比特的芯片，并展示了用于50比特芯片的测量设备，同时也公布了对BeH2分子能量的模拟，表明了在量子计算的研究上紧随Google的步伐，不仅如此，IBM还发布了QISKit的量子软件包，促进了人们通过经典编程语言实现对量子计算机的操控。

2020年，本源量子发布自主研发、自主可控的的新一代超导量子计算机——本源悟源（搭载6比特超导量子处理器夸父 KF C6-130）。

../_images/origin_quantum_computer.jpg

除了美国Google公司和IBM公司外，美国Intel公司和荷兰代尔夫特理工大学也合作设计了17比特和49比特超导量子芯片，并在2018年的CES大会上发布，不过具体的性能参数还有待测试；美国初创公司Rigetti发布了19比特超导量子芯片，并演示了无人监督的机器学习算法，使人们见到了利用量子计算机加速机器学习的曙光。

半导体量子芯片

由于经典计算机主要基于半导体技术，基于半导体开发量子计算也是物理学家研究的重点领域。相比超导量子计算微米级别的比特大小，量子点量子比特所占的空间是纳米级别，类似于大规模集成电路一样，更有希望实现大规模的量子芯片。现在的主要方法是在硅或者砷化镓等半导体材料上制备门控量子点来编码量子比特。编码量子比特的方案多种多样，在半导体系统中主要是通过对电子的电荷或者自旋量子态的控制实现。

与超导量子计算类似，半导体量子计算也正在从科研界转向工业界，2016年，美国芯片巨头Intel公司开始投资代尔夫特理工大学的硅基量子计算研究，目标是在五年内制备出第一个二维表面码结构下的逻辑量子比特；2017年，澳大利亚也组建了硅量子计算公司，目标是五年内制备出第一台10比特硅基量子计算机。

在国内，中国科学技术大学的郭国平研究组在传统的GaAs基量子比特方面积累了成熟的技术，实现了多达3个电荷量子比特的操控和读出，并基于电荷量子比特制备了品质因子更高的杂化量子比特，实现对国际水平的追赶，并为进一步的超越做准备。