使用经典计算机模拟量子线路

量子模拟器是在量子计算领域中具有重要意义的工具，它们为研究人员和开发者提供了模拟和分析量子系统行为的有效手段。 这些工具不仅有助于理解量子算法和量子系统的特性，还能够在实际的量子计算机尚未普及的情况下进行算法设计和验证。

在量子电路的模拟方法中，选择合适的模拟后端非常重要，不同量子线路模拟器的适用场所如下：

全振幅量子虚拟机 ：全振幅模拟器可以同时模拟和存储量子态的全部振幅，但受限于机器的内存条件，量子比特达到50位已是极限，适合低比特高深度的量子线路，比如低比特下的谷歌随机量子线路以及需要获取全部模拟结果的场景等。

部分振幅量子虚拟机 ：部分振幅模拟器依赖于其他模拟器提供的低比特量子线路振幅模拟结果，能模拟更高的比特数量，但能模拟的深度降低，通常用于获取量子态振幅的部分子集模拟结果。

单振幅量子虚拟机 ：单振幅模拟器能模拟更高的量子比特线路图，同时模拟的性能较高，不会随着量子比特数目增加呈指数型增长，但随着线路深度增加，模拟性能急剧下降，同时难以模拟多控制门也是其缺点，该模拟器适用于高比特低深度的量子线路模拟，通常用于快速地模拟获得单个量子态振幅结果。

张量网络量子虚拟机 ：张量网络模拟器与单振幅类似，与单振幅对比，可以模拟多控制门，同时在深度较高的线路模拟上存在性能优势。

量子云虚拟机 ：量子云虚拟机可以将任务提交在远程高性能计算集群上运行，突破本地硬件性能限制，同时支持在真实的量子芯片上运行量子算法。

全振幅量子虚拟机

背景介绍

量子电路的经典模拟对于更好地理解量子计算的操作和行为是至关重要的。这样的模拟使研究人员和开发人员能够评估新量子算法的复杂性，并验证量子设备的有效性。

全振幅模拟是量子计算领域中最经典的模拟方案之一，用于模拟较小规模的量子系统。在这个模拟方案中，可以实现对整个量子系统的状态进行精确模拟，从而获得系统在不同时间点上的演化情况。这个方法的核心思想是表示和跟踪量子态的完整振幅信息，通过密度矩阵或纯态向量来描述量子系统的状态。

对于一个量子比特来说，可以看作是一个两能级系统，量子态 \(|\psi\rangle\) 可以表示为：

\[|\psi\rangle=a_0|0\rangle+a_1|1\rangle\]

其中 \(a_0\) 和 \(a_1\) 是复振幅，并且:

\[\left|a_0\right|^2+\left|a_1\right|^2=1\]

式子中 \(|0\rangle\) 和 \(|1\rangle\) 是两个计算标准正交基态，量子态也可以用如下方法表示

\[\begin{split}|\psi\rangle=a_0\left[\begin{array}{l} 1 \\ 0 \end{array}\right]+a_1\left[\begin{array}{l} 0 \\ 1 \end{array}\right]=\left[\begin{array}{l} a_0 \\ a_1 \end{array}\right]\end{split}\]

对于一个 n-比特量子系统来说，可以通过 \(2^n\) 个振幅来表示

\[|\psi\rangle=a_{0 . \ldots 00}|0 \ldots 00\rangle+a_{0 . \ldots 01}|0 \ldots 01\rangle+\ldots+a_{1 . \ldots 11}|1 \ldots 11\rangle\]

所有振幅满足概率归一化条件，即

\[\sum_i\left|a_i\right|^2=1\]

在量子计算过程中，所有的量子逻辑门可以通过矩阵形式施加到系统中。将单门U施加到第K个量子比特上的过程可以表述为：

\[A=I^{\otimes n-k-1} \otimes U \otimes I^{\otimes k},\]

其中I是 \(2 \times 2\) 的单位矩阵， U是 \(2 \times 2\) 酉矩阵，对于双门操作来说，这个过程是类似的。

可以看出，随着量子比特增加，需要表征的量子态振幅数量随指数增加，具体可以参考如下表，这一问题称为量子霸权。

模拟的量子比特数	全部量子态存储所需的最低内存/GB
26	1
27	1
28	4
29	8
30	16
...	...
48	\(2^{22}\)
49	\(2^{23}\)
50	\(2^{24}\)

当达到50比特及以上时，需要的内存数是一个天文数字，这个问题即所谓的 量子霸权（Quantum Supremacy） ，指量子计算机在某些特定任务上展现出超越经典计算机的能力，即在这些任务上实现了经典计算机无法模拟的优越性能。

这种现象突显了量子计算机在某些领域具有巨大的潜力，因为它们能够在短时间内解决一些经典计算机需要花费数年、数百年甚至更多时间才能解决的问题。

接口介绍

QPanda2中在构造量子虚拟机时有以下几种方式：

init(QMachineType.CPU)  # 使用init,不会返回qvm，会在代码中生成一个全局的qvm
auto qvm = init_quantum_machine(QMachineType.CPU) # 通过接口得到quantum machine对象
qvm = CPUQVM() # 新建一个quantum machine对象

备注

init 和 init_quantum_machine 这两个函数不是线程安全的，不适用于多线程编程，而且其最大的量子比特个数和经典寄存器个数均为默认值25。

设置好配置之后要初始化量子虚拟机：

qvm.init_qvm()

备注

调用 init 和 init_quantum_machine 接口， 就不需要初始化了。

全振幅虚拟机支持计算float与double精度的数据，设置方式如下：

qvm = CPUQVM()
#True: double精度， False: float精度
qvm.init_qvm(True)

下面我们就需要去申请量子比特和经典寄存器。

设置最大量子比特个数

# 设置最大量子比特个数和最大经典寄存器个数
qvm.set_configure(30, 30)

备注

若不设置则默认最大比特为29。

例如我们申请4个量子比特：

qubits = qvm.qAlloc_many(4)

申请一个量子比特时也可以用这个接口：

qubit = qvm.qAlloc()

申请经典寄存器也有类似于申请量子比特的接口，其使用方法和申请量子比特的方法一样，如申请4个经典寄存器的方法：

cbits = qvm.cAlloc_many(4)

申请一个经典寄存器时也可以用这个接口：

cbit = qvm.cAlloc()

在一个量子虚拟机中，申请了几次量子比特或经典寄存器，我们想知道一共申请了多少个量子比特或经典寄存器可以用下面的方法：

num_qubit = qvm.get_allocate_qubit_num() # 申请量子比特的个数
num_cbit = qvm.get_allocate_cmem_num() # 申请经典寄存器的个数

我们该如何使用量子虚拟机来执行量子程序呢？ 可以用下面的方法：

prog = QProg()
prog << H(qubits[0]) << CNOT(qubits[0], qubits[1]) << Measure(qubits[0], cbits[0])

result = qvm.directly_run(prog) # 执行量子程序

如果想多次运行一个量子程序，并得到每次量子程序的结果，除了循环调用 directly_run 方法外， 我们还提供了一个接口 run_with_configuration ，该接口有两种重载方法，具体方法如下：

result = qvm.run_with_configuration(prog, cbits, shots)

一种方法中 prog 为量子程序， cbits 为 ClassicalCondition list， shots 是一个整型数据，为量子程序运行次数。

result = qvm.run_with_configuration(prog, cbits, config)

另一种方法中 prog 为量子程序， cbits 为 ClassicalCondition list, config 是一个字典类型的数据，内容如下：

config = {'shots': 1000}

如果想得到量子程序运行之后各个量子态的振幅值，可以调用 get_qstate 函数获得：

stat = qvm.get_qstate()

量子虚拟机中测量和概率使用方法与 量子测量 和 概率测量 中介绍的相同，在这里就不多做赘述。

实例1

from pyqpanda import *

if __name__ == "__main__":
    qvm = CPUQVM()
    qvm.init_qvm()

    qvm.set_configure(29, 29)
    qubits = qvm.qAlloc_many(4)
    cbits = qvm.cAlloc_many(4)

    # 构建量子程序
    prog = QProg()
    prog << H(qubits[0]) << CNOT(qubits[0], qubits[1]) << Measure(qubits[0], cbits[0])

    # 量子程序运行1000次，并返回测量结果
    result = qvm.run_with_configuration(prog, cbits, 1000)

    # 打印量子态在量子程序多次运行结果中出现的次数
    print(result)
    qvm.finalize()

运行结果：

{'0000': 481, '0001': 519}

备注

这个量子程序的运行结果是不确定的，但其 0000 和 0001 对应的值都应该在500左右。

为了方便使用，pyqpanda还封装了一些面向过程的接口，接口名称和使用方法与上述的基本相同。我们将上面的例子修改为面向过程的接口如下：

实例2

from pyqpanda import *

if __name__ == "__main__":
    init(QMachineType.CPU)
    qubits = qAlloc_many(4)
    cbits = cAlloc_many(4)

    # 构建量子程序
    prog = QProg()
    prog << H(qubits[0]) << CNOT(qubits[0], qubits[1]) << Measure(qubits[0], cbits[0])

    # 量子程序运行1000次，并返回测量结果
    result = run_with_configuration(prog, cbits, 1000)

    # 打印量子态在量子程序多次运行结果中出现的次数
    print(result)
    finalize()

运行结果：

{'0000': 484, '0001': 516}

GPU量子虚拟机

背景介绍

GPU量子模拟器提供了另一种全振幅模拟方案，当涉及到计算密集型任务，如复杂的数学计算、图像处理和机器学习等，GPU的并行处理能力使其比CPU更高效，在量子计算的模拟中的优势体现在以下几点：

1. 并行计算架构 ：GPU并行处理能力源于其设计理念，将多个简单的处理器组合在一起，形成大规模的计算能力。这些处理器可以同时执行多个计算任务，从而在处理大规模数据实现高效的并行计算。而量子态的向量计算中，可以分成不同区块，这些区块之间可以并行。

2. 任务分割和调度 ：GPU在执行任务时，任务调度由GPU驱动程序负责，可以根据任务的需求动态分配处理单元和内存资源，当对大型量子线路模拟时，CPU通常需要预设计算资源分配和调度算法，而GPU可以直接交给GPU驱动程序自动调度。

3. 高效的数据缓存和内存管理 ：GPU具有高速的显存和缓存系统，有助于减少数据访问延迟，提高计算效率。此外，GPU还支持对内存进行多层次管理，以优化数据访问和存储。

4. 高性能编程模型和算法 ：为了方便开发者利用GPU的并行处理能力，GPU厂商提供了多种并行编程模型和工具，如CUDA、OpenCL等，量子计算模拟中的矩阵和线性计算任务能充分发挥性能优势。

接口介绍

class GPUQVM(QuantumMachine)

GPU模拟器类,该类实现了基于GPU计算平台的量子线路模拟。

__init__()

初始化 GPUQVM 类实例。

init_qvm() → None

初始化量子虚拟机。

返回:

无返回值。

run_with_configuration(prog: QVec, shots : int, const NoiseModel& = NoiseModel()) → Dict[str, int]

获取采样测量结果的字典形式。

参数:

• qprog (QProg) -- 要运行的量子程序。

• shots (int) -- 要采样测量的次数。

• noise_model (Noise, optional) -- 噪声模型。默认为空的噪声模型。

返回:

包含测量结果的字典，键为测量结果的二进制字符串，值为对应的次数。

返回类型:

Dict[str, int]

抛出:

run_fail -- 获取测量结果失败。

prob_run_dict(program: QProg, qubit_list: QVec, select_max: int = -1) → Dict[str, float]

运行量子程序并获取测量概率结果的字典形式。

参数:

• program (QProg) -- 要运行的量子程序。

• qubit_list (QVec) -- 用于测量的量子比特列表。

• select_max (int, optional) -- 返回的元素数量上限。默认为 -1，表示无限制。

返回:

包含测量概率的字典，键为测量结果的二进制字符串，值为对应的测量概率。

返回类型:

Dict[str, float]

抛出:

run_fail -- 运行量子程序失败。

prob_run_list(program: QProg, qubit_list: QVec, select_max: int = -1) → List[float]

运行量子程序并获取测量概率结果的列表形式。

参数:

• program (QProg) -- 要运行的量子程序。

• qubit_list (QVec) -- 用于测量的量子比特列表。

• select_max (int, optional) -- 返回的元素数量上限。默认为 -1，表示无限制。

返回:

包含测量概率的列表。

返回类型:

List[float]

抛出:

run_fail -- 运行量子程序失败。

prob_run_tuple_list(program: QProg, qubit_list: QVec, select_max: int = -1) → List[Tuple[int, float]]

运行量子程序并获取测量概率结果的元组列表形式。

参数:

• program (QProg) -- 要运行的量子程序。

• qubit_list (QVec) -- 用于测量的量子比特列表。

• select_max (int, optional) -- 返回的元素数量上限。默认为 -1，表示无限制。

返回:

包含测量概率的元组列表，每个元组包含测量结果的索引和对应的概率。

返回类型:

List[Tuple[int, float]]

抛出:

run_fail -- 运行量子程序失败。

GPU模拟器的使用方法和CPUQVM类似，代码示例如下：

代码示例

from pyqpanda import *
from numpy import pi

if __name__ == "__main__":

    qvm = GPUQVM()
    qvm.init_qvm()

    qvm.set_configure(29, 29)
    q = qvm.qAlloc_many(4)
    c = qvm.cAlloc_many(4)

    # 构建量子程序
    prog = QProg()
    prog << H(q[0])\
            << CNOT(q[0], q[1])\
            << RZ(q[0], pi / 4)\
            << RX(q[2], pi / 4)\
            << CZ(q[0], q[1])\
            << CZ(q[2], q[3])

    measure_prog = QProg()
    measure_prog << prog\
                << Measure(q[0], c[0])\
                << Measure(q[1], c[1])

    # 量子程序运行1000次，并返回测量结果
    measure_result = qvm.run_with_configuration(measure_prog, 1000)

    prob_result = qvm.prob_run_dict(prog, [q[0],q[1]])

    # 打印量子态在量子程序多次运行结果中出现的次数
    print(measure_result)
    print(prob_result)
    qvm.finalize()

运行结果：

{'00': 497, '11': 503}
{'00': 0.5, '01': 0.0, '10': 0.0, '11': 0.5}

备注

使用GPU虚拟机需要本地运行环境有cuda环境

全振幅量子虚拟机噪声模拟

在真实的量子计算机中，受制于量子比特自身的物理特性，常常存在不可避免的计算误差。为了能在量子虚拟机中更好的模拟这种误差，在全振幅虚拟机中， 支持对噪声进行模拟，含噪声模拟的量子虚拟机更贴近真实的量子计算机。我们可以自定义噪声类型影响到的量子比特，自定义逻辑门支持的噪声模型， 通过这些自定义形式，我们使用QPanda2开发量子程序的现实应用程度将更高。

物理背景

纯态，混合态

量子计算中，量子比特使用态矢来表示，在没有噪声的理想状态下，量子比特在逻辑门的演化下一直处于纯态(pure state)：

\[\begin{aligned} |\psi \rangle = |\varphi\rangle = \alpha|0\rangle + \beta|1\rangle \end{aligned}\]

当有噪声干扰时，系统会演化到混合态(mixed state)。混合态 \(|\psi\rangle\) 无法使用纯态的线性叠加来表示，通常用系综(ensemble)来表示：

\[\begin{split}\begin{aligned} \{|\varphi_1\rangle, |\varphi_2\rangle, ..., |\varphi_n\rangle\} \\ \{p_1, p_2, ..., p_n\} \end{aligned}\end{split}\]

系统 \(|\psi\rangle\) 的最终状态，以 \(p_1\) 的概率处于纯态 \(|\varphi_1\rangle = \alpha_1|0\rangle + \beta_1|1\rangle\) ，以 \(p_2\) 的概率处于纯态 \(|\varphi_2\rangle= \alpha_2|0\rangle + \beta_2|1\rangle\) ，以此类推。

混合态不是纯态的线性叠加。假设系统处于 \(\{|0\rangle, |1\rangle\}，\{\frac{1}{2},\frac{1}{2}\}\) 的混合态， 那么系统最终的状态，50%的概率处于 \(|0\rangle\), 50%的概率处于 \(|1\rangle\)。 多次重复测量得到的结果与态 \(\frac{1}{\sqrt 2}|0\rangle + \frac{1}{\sqrt 2}|1\rangle\) 相同，但两者的量子态却完全不同。

噪声对系统的演化

量子计算机，作为一个孤立系统，不受外界干扰时，一直处于纯态。当外界噪音干扰与计算机比特耦合之后，计算机加上外界整个系统处于纯态。但对于计算机这个系统，则其处于混合态。

我们可以用一个简单的模型来等效演示

初始态两比特为 \(|\psi_{1}\psi_0\rangle\) ，其中，\(|\psi_0\rangle\) 代表我们的量子计算机系统， \(|\psi_1\rangle\) 表示外界。当外界对计算机无干扰时，\(|\psi_0\rangle\) 是个孤立系统，当逻辑门施加在 \(|\psi_0\rangle\) 上时，其始终为纯态。 如果模拟外界对量子计算机的干扰，将两个比特制备为纠缠态，即外界对计算机造成了噪声干扰。对于两个比特的整个系统来讲，仍然处于纯态。此时整个系统处于

\[|\psi_{1}\psi_0\rangle = \frac{1}{\sqrt{2}}|00\rangle+\frac{1}{{\sqrt{2}}}|11\rangle\]

但当只看0比特位时，即我们的量子计算机，其态矢不能从中分离出来，表示为纯态的线性叠加，\(|\psi_0\rangle\neq\frac{1}{\sqrt{2}}|0\rangle+\frac{1}{{\sqrt{2}}}|1\rangle\), 此时单独对于 \(|\psi_0\rangle\) 来讲，其已经处于混合态（由约化密度矩阵可知）。测量得到50%概率为 \(|0\rangle\)， 50%的概率为 \(|1\rangle\)。

噪声对包含计算机和环境的整个系统的演化算子是酉的，但仅对于计算机量子态的来看，则可能是非酉的。 因此，对于噪声对计算机系统量子态的演化，通常使用算子和表示(operator-sum representation)：

\[\rho^{\prime} = \sum\limits_{i}{K_i}{\rho} {K_i}^{\dagger}\]

其中 \(K_i\) 为表示噪声演化的Kraus算子，满足

\[\sum\limits_{i}K_{i}^{\dagger} K_{i} = 1\]

噪声模型介绍

QPanda2为我们提供了丰富的噪声模型，我们可以自定义噪声模型和量子逻辑门的对应关系。噪声模型主要分为两种：单门噪声模型和双门噪声模型。

单门噪声模型

DAMPING_KRAUS_OPERATOR

DAMPING_KRAUS_OPERATOR是量子比特的弛豫过程噪声模型，它的kraus算符和表示方法如下所示：

\(K_1 = \begin{bmatrix} 1 & 0 \\ 0 & \sqrt{1 - p} \end{bmatrix}, K_2 = \begin{bmatrix} 0 & \sqrt{p} \\ 0 & 0 \end{bmatrix}\)

需要一个噪声参数 \(p\) ，为取值 \([0, 1]\) 之间的实数，意义为发生噪声影响的概率。

假设初始态处于 \(|\psi\rangle = \frac{1}{\sqrt 2}|0\rangle + \frac{1}{\sqrt 2}|1\rangle\) 使用算子和表示来演化噪声的影响：

\[\begin{split}\rho^{\prime} = K_1\rho K_{1}^{\dagger} + K_2\rho K_{2}^{\dagger} = \frac{1}{2} \begin{bmatrix} 1+p & \sqrt{1 - p}\\ \sqrt{1 - p} & 1 - p \end{bmatrix}\end{split}\]

测量得到结果的概率分别为：

\[\begin{split}\begin{aligned} p(|0\rangle) = \frac{1}{2}(1+p) \\ p(|1\rangle) = \frac{1}{2}(1-p) \end{aligned}\end{split}\]

由 \(tr(\rho^2) = \frac{1}{2}(2-p+p^2)\) 可见，当 \(p=0\) 或 \(1\) 时，系统仍为纯态；当 \(p=(0, 1)\) 时，系统处于混合态。 可见，当 \(p\) 为 \(0\) 时，即没有噪声影响，量子态保持不变；若 \(p\) 为 \(1\) 时，必定发生弛豫，演化为态 \(|0\rangle\)。

后面的噪声演化过程不再演示，读者可以自行演算。

DEPHASING_KRAUS_OPERATOR

DEPHASING_KRAUS_OPERATOR是量子比特的退相位过程噪声模型，它的kraus算符和表示方法如下所示：

\(K_1 = \begin{bmatrix} \sqrt{1 - p} & 0 \\ 0 & \sqrt{1 - p} \end{bmatrix}, K_2 = \begin{bmatrix} \sqrt{p} & 0 \\ 0 & -\sqrt{p} \end{bmatrix}\)

需要一个噪声参数。

DECOHERENCE_KRAUS_OPERATOR

DECOHERENCE_KRAUS_OPERATOR是退相干噪声模型，为上述两种噪声模型的综合，他们的关系如下所示：

\(P_{damping} = 1 - e^{-\frac{t_{gate}}{T_1}}, P_{dephasing} = 0.5 \times (1 - e^{-(\frac{t_{gate}}{T_2} - \frac{t_{gate}}{2T_1})})\)

\(K_1 = K_{1_{damping}}K_{1_{dephasing}}, K_2 = K_{1_{damping}}K_{2_{dephasing}},\)

\(K_3 = K_{2_{damping}}K_{1_{dephasing}}, K_4 = K_{2_{damping}}K_{2_{dephasing}}\)

该噪声模型需要三个参数， T1,T2和量子门时间参数 ，p0和p1的形式如下：

\[\begin{split}\begin{array}{c} p 0=p_{\text {damping}}=1-e^{-\frac{t_{\text {gate}}}{T_{1}}} \\ p 1=p_{\text {dephasing}}=0.5 *\left(1-e^{-\left(\frac{t_{\text {gate}}}{T_{2}}-\frac{t_{\text {gate}}}{2 T_{1}}\right)}\right) \end{array}\end{split}\]

噪声参数的范围如下:

\[T_{1} \in[5,100], T_{2} \in\left[2,2 T_{1}\right]\]

DEPOLARIZING_KRAUS_OPERATOR

DEPOLARIZING_KRAUS_OPERATOR去极化噪声模型，即单量子比特有一定的概率被完全混合态I/2代替, 它的kraus算符和表示方法如下所示：

\(K_1 = \sqrt{1 - 3p/4} × I, K_2 = \sqrt{p}/2 × X\)

\(K_3 = \sqrt{p}/2 × Y, K_4 = \sqrt{p}/2 × Z\)

其中I、X、Y、Z分别代表其量子逻辑门对应的矩阵

需要一个噪声参数

BITFLIP_KRAUS_OPERATOR

BITFLIP_KRAUS_OPERATOR是比特反转噪声模型，它的kraus算符和表示方法如下所示：

\(K_1 = \begin{bmatrix} \sqrt{1 - p} & 0 \\ 0 & \sqrt{1 - p} \end{bmatrix}, K_2 = \begin{bmatrix} 0 & \sqrt{p} \\ \sqrt{p} & 0 \end{bmatrix}\)

需要一个噪声参数。

BIT_PHASE_FLIP_OPRATOR

BIT_PHASE_FLIP_OPRATOR是比特-相位反转噪声模型，它的kraus算符和表示方法如下所示：

\(K_1 = \begin{bmatrix} \sqrt{1 - p} & 0 \\ 0 & \sqrt{1 - p} \end{bmatrix}, K_2 = \begin{bmatrix} 0 & -i \times \sqrt{p} \\ i \times \sqrt{p} & 0 \end{bmatrix}\)

需要一个噪声参数。

PHASE_DAMPING_OPRATOR

PHASE_DAMPING_OPRATOR是相位阻尼噪声模型，它的kraus算符和表示方法如下所示：

\(K_1 = \begin{bmatrix} 1 & 0 \\ 0 & \sqrt{1 - p} \end{bmatrix}, K_2 = \begin{bmatrix} 0 & 0 \\ 0 & \sqrt{p} \end{bmatrix}\)

需要一个噪声参数。

双门噪声模型

双门噪声模型同样也分为上述几种：DAMPING_KRAUS_OPERATOR、DEPHASING_KRAUS_OPERATOR、DECOHERENCE_KRAUS_OPERATOR、DEPOLARIZING_KRAUS_OPERATOR、BITFLIP_KRAUS_OPERATOR、BIT_PHASE_FLIP_OPRATOR、PHASE_DAMPING_OPRATOR。 它们的输入参数与单门噪声模型一致，双门噪声模型的kraus算符和表示与单门噪声模型存在着对应关系：假设单门噪声模型为： \(\{ K1, K2 \}\) ，那么对应的双门噪声模型为 \(\{K1\otimes K1, K1\otimes K2, K2\otimes K1, K2\otimes K2\}\)。

接口介绍

全振幅虚拟机在进行含噪声模拟时，只需要在初始化前设置一些量子逻辑门的噪声模型和对应的参数即可。

目前QPanda2中含噪声量子逻辑门支持的噪声模型有：

class NoiseModel:
    BITFLIP_KRAUS_OPERATOR
    BIT_PHASE_FLIP_OPRATOR
    DAMPING_KRAUS_OPERATOR
    DECOHERENCE_KRAUS_OPERATOR
    DEPHASING_KRAUS_OPERATOR
    DEPOLARIZING_KRAUS_OPERATOR
    PHASE_DAMPING_OPRATOR

使用 Noise 类接口设置噪声模型参数：

def add_noise_model(self, noise_model: NoiseModel, gate_type: GateType, prob: float) -> None:
def add_noise_model(self, noise_model: NoiseModel, gate_types: List[GateType], prob: float) -> None:
def add_noise_model(self, noise_model: NoiseModel, gate_type: GateType, prob: float, qubits: QVec) -> None:
def add_noise_model(self, noise_model: NoiseModel, gate_types: List[GateType], prob: float, qubits: QVec) -> None:
def add_noise_model(self, noise_model: NoiseModel, gate_type: GateType, prob: float, qubits: List[QVec]) -> None:

第一个参数为噪声模型类型，第二个参数为量子逻辑门类型，第三个参数为噪声模型所需的参数, 第四个参数是对单个比特设置噪声参数（包含单门和双门），若没有第四个参数则对所有的比特设置相应的噪声模型。

对于需要输入三个参数的噪声类型，接口如下：

def add_noise_model(self, noise_model: NoiseModel, gate_type: GateType, t1: float, t2: float, t_gate: float) -> None:
def add_noise_model(self, noise_model: NoiseModel, gate_types: List[GateType], t1: float, t2: float, t_gate: float) -> None:
def add_noise_model(self, noise_model: NoiseModel, gate_type: GateType, t1: float, t2: float, t_gate: float, qubits: QVec) -> None:
def add_noise_model(self, noise_model: NoiseModel, gate_types: List[GateType], t1: float, t2: float, t_gate: float, qubits: QVec) -> None:
def add_noise_model(self, noise_model: NoiseModel, gate_type: GateType, t1: float, t2: float, t_gate: float, qubits: List[QVec]) -> None:

接口参数意义与之前的接口类似

除此之外，噪声模型还支持设置测量噪声,表示执行测量操作本身带入到系统的噪声，与单门操作触发的算子噪声类似，

def add_measure_error(self, noise_model: NoiseModel, prob: float, qubits: QVec = ...) -> None:
def add_measure_error(self, noise_model: NoiseModel, t1: float, t2: float, t_gate: float, qubits: QVec = ...) -> None:

用法类似于量子逻辑门的噪声模型，第一个参数为噪声模型类型，后面的参数和量子逻辑门的噪声参数。

重置噪声：

def set_reset_error(self, p0: float, p1: float, qubits: QVec) -> None:

p0 表示重置到 \(\left|0\right\rangle\) 的概率，p1表示重置到 \(\left|1\right\rangle\) 的概率，未被重置的概率为 1-p0-p1。

读出噪声：

def set_readout_error(self, prob_list: List[List[float]], qubits: QVec = ...) -> None:

probs_list 为四个元素，两两一组，如 probs_list = {{f0, 1 - f0},{1 - f1, f1}};， 表示当测量终态为 \(\left|0\right\rangle\) ，读出为0的概率为f0，读出为1的概率为1-f0；当测量终态为 \(\left|1\right\rangle\) 时，读出为0的概率为1-f1，读出为1的概率为f1。

第二个参数为读出噪声作用的比特。

读出噪声不是量子噪声，而是经典仪器从低温量子态获取到结果，到室温过程中环境造成的干扰。

噪声模型还支持设置带有相位角旋转的量子逻辑门的旋转误差，其接口使用方式如下：

def set_rotation_error(self, error: float) -> None:

实例

from pyqpanda import *
import numpy as np

if __name__ == "__main__":
    qvm = CPUQVM()
    qvm.init_qvm()
    q = qvm.qAlloc_many(4)
    c = qvm.cAlloc_many(4)

    # 创建噪声模型，并添加设置噪声参数
    noise = Noise()
    noise.add_noise_model(NoiseModel.BITFLIP_KRAUS_OPERATOR, GateType.PAULI_X_GATE, 0.1)
    qv0 = [q[0], q[1]]
    noise.add_noise_model(NoiseModel.DEPHASING_KRAUS_OPERATOR, GateType.HADAMARD_GATE, 0.1, qv0)
    qves = [[q[0], q[1]], [q[1], q[2]]]
    noise.add_noise_model(NoiseModel.DAMPING_KRAUS_OPERATOR, GateType.CNOT_GATE, 0.1, qves)

    f0 = 0.9
    f1 = 0.85
    noise.set_readout_error([[f0, 1 - f0], [1 - f1, f1]])
    noise.set_rotation_error(0.05)

    prog = QProg()
    prog << X(q[0]) << H(q[0]) \
         << CNOT(q[0], q[1]) \
         << CNOT(q[1], q[2]) \
         << CNOT(q[2], q[3]) \
         << measure_all(q, c)

    # 运行量子程序时，加入噪声模型。默认为空噪声模型，即无噪声
    result = qvm.run_with_configuration(prog, c, 1000, noise)
    print(result)

运行结果：

{'0000': 347, '0001': 55, '0010': 50, '0011': 43, '0100': 41, '0101': 18, '0110': 16, '0111': 34, '1000': 50, '1001': 18, '1010': 18, '1011': 37, '1100': 15, '1101': 49, '1110': 42, '1111': 167}

程序在无噪声的理想情况下，结果应该当为等概率的 0000 和 1111。结果中的其他测量值，为噪声带来的影响。

部分振幅量子虚拟机

目前用经典计算机模拟量子虚拟机的主流解决方案有全振幅与单振幅两种。除此之外，还有部分振幅量子虚拟机，该方案[1]能在更低的硬件条件下，实现更高的模拟效率。

背景介绍

在过去的几年里，半导体量子芯片也取得了很大进展[3-5]。量子霸权声称如果制造出一个由50个量子位组成的装置，经典计算机的极限将被超越（即直接模拟50个量子位需要大约16-PB的RAM来存储完整的向量）。

Google和ibm团队已经提出了一些有效的方法来模拟49量子位以上的低深度电路(例如延迟纠缠门)[2]。

在这里我们提出了一种优化低深度大采样数量子电路经典模拟的方案并对其进行了64量子位模拟。

具体来说，大致方案是通过将几个控制Z (CZ)门变换为测量门和单量子位门，将电路映射到多个额外的子电路中。

这些子电路由两个块组成，它们之间没有任何量子比特纠缠，从而将 一个N量子比特的模拟问题转化为一组N/2的电路求解问题 。

我们的方法是类似于二维网格的平衡切割，对于一个CZ门，分裂成四个子电路，然后将所有子电路的结果相加，以重建最终状态。

模拟方案细节

部分振幅量子虚拟机的基本思想是将大比特的量子程序拆分成若干个小比特量子程序，每个小比特量子线路使用全振幅算法计算，量子程序的拆分规则如下： 若量子线路中出现跨节点的双量子逻辑门，则对量子程序进行拆分。即以量子程序中量子比特数为总量子比特数的一半或接近一半为分界线，例如总量子比特数为10，则4号比特与5号比特之间为分界线。 双量子逻辑门的控制位量子比特与目标位量子比特分别处于界线的两侧，称为跨节点，例如总量子比特数为10，CNOT(1,5)为跨节点，CNOT(1,4)则没有跨节点。

一个CZ门可以转化为两组测量门和单量子位门的组合，具体的

\[\mathrm{CZ}=P_0 \times I+P_1 \times Z\]

其中I表示单位矩阵,Z表示Pauli-Z矩阵

\[\begin{split}P_0=\left(\begin{array}{ll}1 & 0 \\ 0 & 0\end{array}\right) P_1=\left(\begin{array}{ll}0 & 0 \\ 0 & 1\end{array}\right)\end{split}\]

对于其他双量子逻辑门，如CR、iSWAP、SqiSWAP等， 可以通过量子逻辑门转化算法将其转换成单量子逻辑门和支持拆分的双量子逻辑门的组合，再对双量子逻辑门进行拆分，拆分过程的示例图如下：

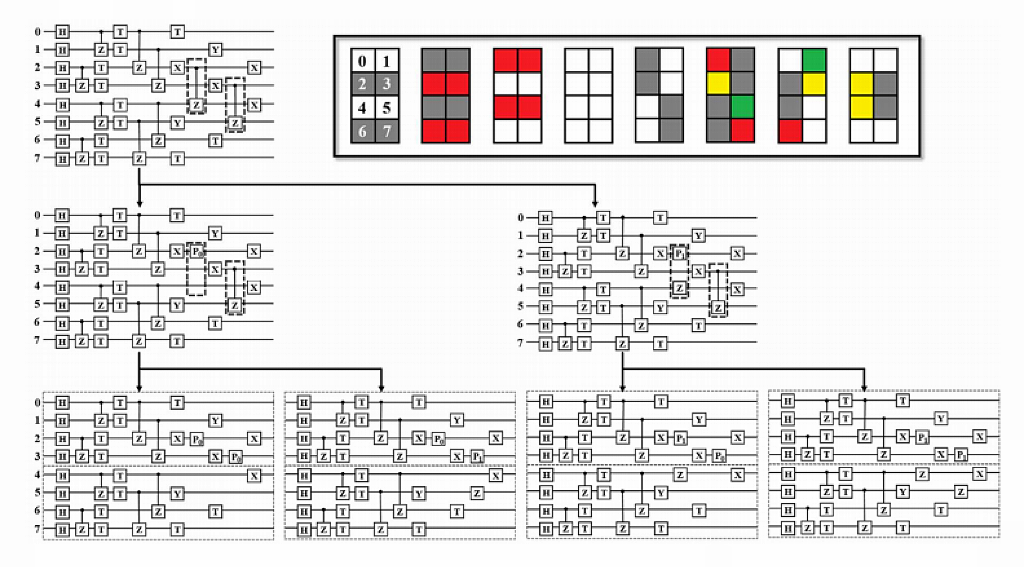
上图是拆分的一个例子。第一行是原来的电路。框中的两个CZ门将前四位和最后四位纠缠在一起。接着，转换左CZ门，原电路等效于第二行电路的加法。继续右CZ门被转换，在第三行产生四个电路。原电路的最终状态等于所有变换电路的加法。第三行中的虚线将每个电路分成两部分，在两部分中可以独立地进行模拟。

使用介绍

class PartialAmpQVM(QuantumMachine)

量子部分振幅模拟器类,该类实现了基于部分振幅拆分图算法的量子线路模拟。

__init__()

初始化 PartialAmpQVM 类实例。

get_prob_dict(qubit_list: QVec) → Dict[str, float]

获取测量概率结果的字典形式。

参数:

qubit_list (QVec) -- 用于测量的量子比特列表。

返回:

包含测量概率的字典，键为测量结果的二进制字符串，值为对应的测量概率。

返回类型:

Dict[str, float]

抛出:

run_fail -- 获取测量概率失败。

init_qvm(type: BackendType = BackendType.CPU) → None

初始化量子虚拟机。

参数:

type (BackendType, optional) -- 子图计算后端的类型。默认为 BackendType.CPU。

返回:

无返回值。

pmeasure_bin_index(bin_index: str) → complex

获取指定二进制索引的量子态振幅。

参数:

bin_index (str) -- 二进制索引。

返回:

指定二进制索引的量子态振幅。

返回类型:

complex

抛出:

run_fail -- 获取振幅失败。

pmeasure_dec_index(dec_index: str) → complex

获取指定十进制索引的量子态振幅。

参数:

dec_index (str) -- 十进制索引。

返回:

指定十进制索引的量子态振幅。

返回类型:

complex

抛出:

run_fail -- 获取振幅失败。

pmeasure_subset(index_list: List[str]) → Dict[str, complex]

获取量子态部分子集的振幅。

参数:

index_list (List[str]) -- 量子态索引列表。

返回:

包含量子态子集振幅的字典，键为量子态索引，值为对应的量子态振幅。

返回类型:

Dict[str, complex]

抛出:

run_fail -- 获取振幅失败。

run(qprog: QProg, noise_model: Noise = NoiseModel()) → None

运行量子程序，拆分原始线路，生成子图。

参数:

• qprog (QProg) -- 要运行的量子程序。

• noise_model (Noise, optional) -- 噪声模型。默认为空的噪声模型。

返回:

无返回值。

抛出:

run_fail -- 运行量子程序失败。

其使用方式与前面介绍的量子虚拟机模块非常类似，首先通过 PartialAmpQVM 初始化一个部分振幅量子虚拟机对象用于管理后续一系列行为

from pyqpanda import *
from numpy import pi
machine = PartialAmpQVM()

然后是量子程序的初始化、构建与装载过程，以QPanda2的部分振幅示例程序来演示：

machine.init_qvm()

q = machine.qAlloc_many(10)
c = machine.cAlloc_many(10)

# 构建量子程序
prog = QProg()
prog << hadamard_circuit(q)\
     << CZ(q[1], q[5])\
     << CZ(q[3], q[7])\
     << CZ(q[0], q[4])\
     << RZ(q[7], pi / 4)\
     << RX(q[5], pi / 4)\
     << RX(q[4], pi / 4)\
     << RY(q[3], pi / 4)\
     << CZ(q[2], q[6])\
     << RZ(q[3], pi / 4)\
     << RZ(q[8], pi / 4)\
     << CZ(q[9], q[5])\
     << RY(q[2], pi / 4)\
     << RZ(q[9], pi / 4)\
     << CZ(q[2], q[3])

machine.run(prog)

部分接口使用如下：

• pmeasure_bin_index(string) ,使用示例

  result = machine.pmeasure_bin_index("0000000000")
  print(result)
  

  结果输出如下：

  (-0.00647208746522665-0.006472080945968628j)
  

• pmeasure_dec_index(string) ,使用示例

  result = machine.pmeasure_dec_index("1")
  print(result)
  

  结果输出如下：

  (-4.413170804465268e-19-0.009152913087920392j)
  

• pmeasure_subset(state_index) ,使用示例

  state_index = ["0", "1", "2"]
  result = machine.pmeasure_subset(state_index)
  print(result)
  

  结果输出如下：

  {'0': (-0.006472086912079613-0.00647208691207961j),
   '1': (-4.413170804465268e-19-0.009152913087920392j),
   '2': (-3.0357660829594124e-18-0.009152913087920392j)}
  

参考文献

[1] 64-qubit quantum circuit simulation Zhao-Yun Chen1,Qi Zhou,Cheng Xue,Guang-Can Guo,Guo-PingGuo(2020).
[2] Pednault E, Gunnels JA, Nannicini G, et al. Breaking the 49-qubit barrier in the simulation of quantum circuits. Preprint at https://arxiv.org/abs/1710.05867v1 (2017).
[3] Cao G, Li HO, Tu T, et al. Ultrafast universal quantum control of a quantum-dot charge qubit using Landau-Zener-Stuckelberg interference. Nat Commun 4: 1401 (2013).
[4] Li HO, Cao G, Yu GD, et al. Conditional rotation of two strongly coupled semiconductor charge qubits. Nat Commun 6: 7681 (2015).
[5] Li HO, Cao G, Yu GD, et al. Controlled quantum operations of a semiconductor three-qubit System. Phys Rev A 9: 024015 (2018).

单振幅量子虚拟机

短期内，量子霸权的存在，超出了现有经典算法在最先进计算机或超算上的能力，这刺激了最近在模拟量子电路的经典算法方面的进展。

与适用于低比特高深度的全向量模拟相比，单振幅模拟器将量子电路的模拟推广到一个无向图形模型上，并在精确推理的背景下，利用变量消去算法进行了计算。

首先我们在量子线路演化中引入费曼路径积分方法。

我们用酉矩阵的乘积来表示量子电路 \(U^{(t)}\) ，其中t表示不同的时钟周期。

在电路的最后一个周期后，我们引入以下符号来表示特定量子位串的振幅。

\[\langle x|\mathcal{U}| 0 \ldots 0\rangle=\sum_{\left\{b^t\right\}} \prod_{t=0}^{d-1}\left\langle b^{t+1}\left|U^{(t)}\right| b^t\right\rangle, \quad\left|b^d\right\rangle=|x\rangle\]

这里 \(\left|b^t\right\rangle=\otimes_{j=1}^n\left|b_j^t\right\rangle\) ，以及 \(\left|b_i^t\right\rangle\) 对应量子态 \(|0\rangle\) 或 \(|1\rangle\) 的第 \(j\)-th 比特。

上述表达式可以看作是n量子位系统的 \(\left\{b^0, \ldots, b^d\right\}\) 的费曼路径积分形式。

根据上文所说，一个量子线路是多个酉矩阵的乘积，即 \(\mathcal{U}=U_g \cdots U_1\) ，其中对于一个对角矩阵可以用如下表述：

\[U=\sum_{b \in\{0,1\}} \psi_U(b)|b\rangle\langle b| \quad \text { (diagonal) }\]

其中 \(\psi_U(b)\) 是一个布尔变量的复函数，对于一个非对角矩阵，比如 \(\mathrm{H}, \mathrm{X}^{1 / 2}, \mathrm{Y}^{1 / 2}\) ,有

\[U=\sum_{b, b^{\prime} \in\{0,1\}} \psi_U\left(b^{\prime}, b\right)\left|b^{\prime}\right\rangle\langle b| \quad \text { (non-diagonal) }\]

其中 \(\psi_U\left(b, b^{\prime}\right)\) 是两个布尔变量的复函数，例如对于一个H门， \(\psi_{\mathrm{H}}(1,1)= -1 / \sqrt{2}\) , 其他项等于 \(1 / \sqrt{2}\) 。 一个对角双门，例如CZ，可以写成如下形式

\[U=\mathrm{CZ}=\sum_{b, b^{\prime} \in\{0,1\}} \psi_{\mathrm{CZ}}\left(b, b^{\prime}\right)\left|b, b^{\prime}\right\rangle\left\langle b, b^{\prime}\right|,\]

根据对角矩阵和非对角矩阵的性质，可以在有向无环图中分别用不同形状表示，以如下量子线路为例

假设以初态 \(| 00\rangle\) 计算量子态末态为 \(| 00\rangle\) 的概率，对应的有向无环图模型为

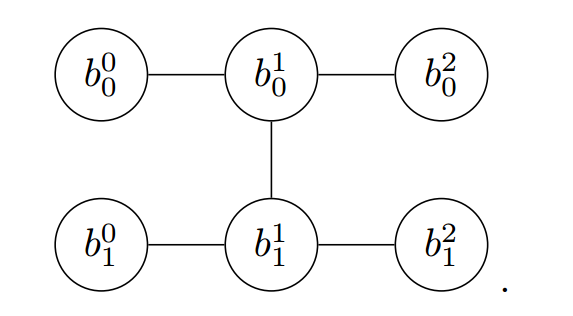
因为初态和末态是确定的，我们有 \(b_0^0=b_0^2=b_1^0=b_1^2=0\) 。图可以简化为如下形式：

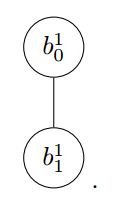
这个图的树宽为2 ,我们可以计算出

\[\begin{split}\begin{array}{r} \langle 00|C| 00\rangle=\sum_{b_0^1, b_1^1} \psi_{\mathrm{H}}\left(0, b_0^1\right) \psi_{\mathrm{CZ}}\left(b_0^1, b_1^1\right) \psi_{\mathrm{H}}\left(b_0^1, 0\right) \\ \psi_{\mathrm{H}}\left(0, b_1^1\right) \psi_{\mathrm{H}}\left(b_1^1, 0\right) . \end{array}\end{split}\]

函数 \(\psi_{\mathrm{H}}\) 对应的H门映射表可以写为

\[\begin{split}\begin{array}{|ll|c|} \hline 0 & 0 & 1 / \sqrt{2} \\ 0 & 1 & 1 / \sqrt{2} \\ 1 & 0 & 1 / \sqrt{2} \\ 1 & 1 & -1 / \sqrt{2} \\ \hline \end{array}\end{split}\]

函数 \(\psi_{\mathrm{CZ}}\) 对应的CZ门映射表可以写为

\[\begin{split}\begin{array}{|ll|c|} \hline 0 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & -1 \\ \hline \end{array}\end{split}\]

上面的等式就可以重写为

\[\langle 00|C| 00\rangle=\sum_{b_0^1, b_1^1} \tau_1\left(b_0^1, b_1^1\right)\]

其中表中 \(\tau_1\) 的映射关系为

\[\begin{split}\begin{array}{|ll|c|} \hline 0 & 0 & 1 / 4 \\ 0 & 1 & 1 / 4 \\ 1 & 0 & 1 / 4 \\ 1 & 1 & -1 / 4 \\ \hline \end{array}\end{split}\]

如果我们把所有的 \(b_1^1\) 相加可以得到

\[\langle 00|C| 00\rangle=\sum_{b_0^1} \tau_2\left(b_0^1\right)\]

其中 \(\tau_2\) 为

\[\begin{split}\begin{array}{|c|c|} \hline 0 & 1 / 2 \\ 1 & 0 \\ \hline \end{array}\end{split}\]

最终， 对 \(b_0^1\) 求和，可以计算出末态的概率

\[\langle 00|C| 00\rangle=1 / 2 .\]

class SingleAmpQVM(QuantumMachine)

量子单振幅模拟器类

该类实现了基于单振幅的量子线路模拟，借助于费曼积分路径和quickBB，可以快速模拟大比特稀疏量子线路的单个振幅

__init__()

初始化单振幅模拟器类实例。

pmeasure_bin_amplitude(bin_string: str) → complex

获取指定二进制字符串的量子态振幅。

参数:

bin_string (str) -- 二进制字符串。

返回:

指定二进制字符串的量子态振幅。

返回类型:

complex

抛出:

run_fail -- 获取振幅失败。

pmeasure_bin_index(bin_string: str) → float

获取指定二进制字符串的量子态概率振幅。

参数:

bin_string (str) -- 二进制字符串。

返回:

指定二进制字符串的量子态概率振幅。

返回类型:

float

抛出:

run_fail -- 获取概率振幅失败。

pmeasure_dec_amplitude(dec_string: str) → complex

获取指定十进制字符串的量子态振幅。

参数:

dec_string (str) -- 十进制字符串。

返回:

指定十进制字符串的量子态振幅。

返回类型:

complex

抛出:

run_fail -- 获取振幅失败。

pmeasure_dec_index(dec_string: str) → float

获取指定十进制字符串的量子态概率振幅。

参数:

dec_string (str) -- 十进制字符串。

返回:

指定十进制字符串的量子态概率振幅。

返回类型:

float

抛出:

run_fail -- 获取概率振幅失败。

run(prog: QProg, qubit_list: QVec, max_rank: int = 30, alloted_time: int = 5) → None

运行量子程序。

参数:

• prog (QProg) -- 要运行的量子程序。

• qubit_list (QVec) -- 用于运行的量子比特列表。

• max_rank (int, optional) -- 最大秩限制。默认为 30。

• alloted_time (int, optional) -- 允许quickBB的运行时间。默认为 5。

返回:

无返回

其使用方式与前面介绍的量子虚拟机模块非常类似，首先通过 SingleAmpQVM 初始化一个单振幅量子虚拟机对象用于管理后续一系列行为。

from pyqpanda import *
from numpy import pi

qvm = SingleAmpQVM()

然后是量子程序的初始化、构建与装载过程：

qvm.init_qvm()

qv = qvm.qAlloc_many(10)
cv = qvm.cAlloc_many(10)

prog = QProg()

# 构建量子程序
prog << CZ(qv[1], qv[5])\
    << CZ(qv[3], qv[5])\
    << CZ(qv[2], qv[4])\
    << CZ(qv[3], qv[7])\
    << CZ(qv[0], qv[4])\
    << RY(qv[7], pi / 2)\
    << RX(qv[8], pi / 2)\
    << RX(qv[9], pi / 2)\
    << CR(qv[0], qv[1], pi)\
    << CR(qv[2], qv[3], pi)\
    << RY(qv[4], pi / 2)\
    << RZ(qv[5], pi / 4)\
    << RX(qv[6], pi / 2)\
    << RZ(qv[7], pi / 4)\
    << CR(qv[8], qv[9], pi)\
    << CR(qv[1], qv[2], pi)\
    << RY(qv[3], pi / 2)\
    << RX(qv[4], pi / 2)\
    << RX(qv[5], pi / 2)\
    << CR(qv[9], qv[1], pi)\
    << RY(qv[1], pi / 2)\
    << RY(qv[2], pi / 2)\
    << RZ(qv[3], pi / 4)\
    << CR(qv[7], qv[8], pi)

然后是调用计算接口，需要注意的是， run 方法是调用计算振幅前必须调用的函数，用于正确生成有向无环图和计算路径，

pmeasure_bin_index ,使用时需要结合 run 方法。用法示例：

# run 有三个参数，默认2个，
# 第一个执行的量子程序
# 第二个为申请的量子比特
# 第三个为最大RANK，这里根据内存设置，默认30
# 第四个就是quickBB优化的最大运行时间，默认5s

qvm.run(prog, qv)
bin_result = qvm.pmeasure_bin_index("0001000000")
print("0001000000 : ", bin_result)

结果输出如下：

0001000000 :  0.001953123603016138

pmeasure_dec_index ,使用时需要结合 run 方法。用法示例：

qvm.run(prog, qv)
dec_result = qvm.pmeasure_dec_index("2")
print("2 : ",dec_result)

结果输出如下：

2 :  0.001953123603016138

张量网络量子虚拟机

对于一个 \(N\) 个量子比特的自旋体系，对应的希尔伯特空间维数为 \(2^{N}\) 。

对于该复杂系统的状态演化，传统的全振幅模拟器将其看做一个有 \(2^{N}\) 个元素的一维向量。

然而从张量网络的角度来看，整个系统量子态的系数对应 \(2^{N}\) 维张量（即N阶张量，即有 \(N\) 个指标，每个指标的维数是2），量子操作算符的系数为 \(2^{2N}\) 维张量（ \(2N\) 阶张量，即有个 \(2N\) 指标，每个指标的维数是2），我们可以用如下图形来表示量子态：

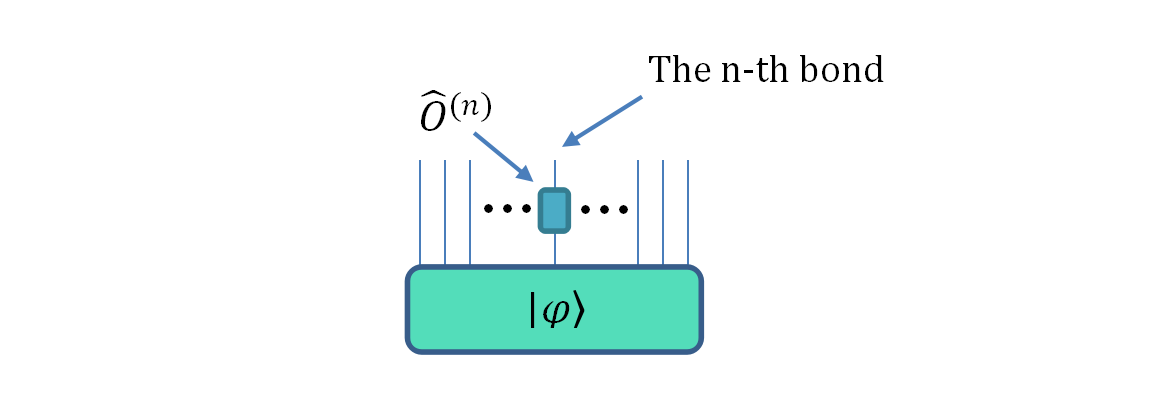
当量子系统的自旋个数增加时，量子态系数的个数随指数增加，称为指数墙问题，这一障碍限制了传统全振幅模拟器的最大模拟自旋数和模拟性能。

但是可通过张量网络处理这一问题，从而绕过指数墙障碍，在张量网络中，我们对量子系统的模拟，包括量子逻辑门操作和测量操作，均可以通过对于张量的缩并与分解来实现。矩阵乘积态是张量网络中最常用的表示形式，在多线性代数中称为张量列或TT（Tensor-Train），示意图如下。

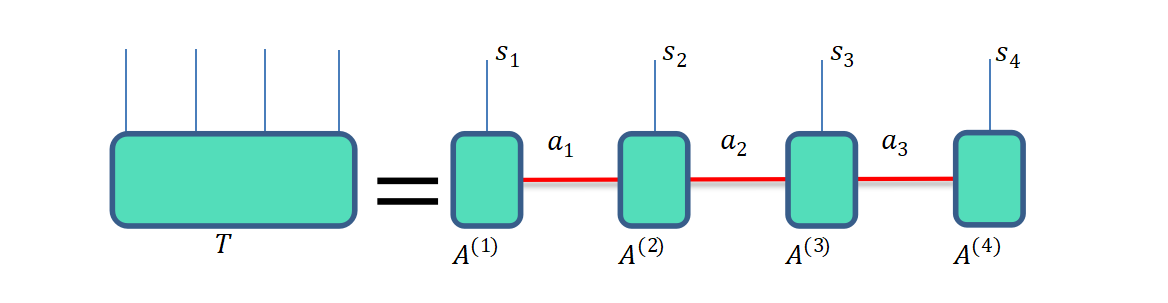
将量子态分解成等式右边的表示形式，对于量子线路中部分量子逻辑门操作，可以将全局问题转化为局部的张量处理问题，从而有效地降低了时间复杂度和空间复杂度。

pyqpanda 中可以通过 MPSQVM 类实现用张量网络模拟量子电路。

class MPSQVM(QuantumMachine)

该类实现了基于矩阵乘积态（MPS）的量子线路模拟。可以获取测量结果、模拟量子态等操作。

__init__()

初始化 MPSQVM 类实例。

pmeasure(qubit_list: QVec, select_max: int = -1) → List[Tuple[int, float]]

获取量子测量概率分布的列表形式。

参数:

• qubit_list (QVec) -- 用于测量的量子比特列表。

• select_max (int, optional) -- 返回的元素数量上限。默认为 -1，表示无限制。

返回:

包含量子测量结果的列表，每个元组包含测量结果的索引和对应的概率。

返回类型:

List[Tuple[int, float]]

pmeasure_bin_index(program: QProg, string: str) → complex

获取指定二进制字符串的量子态振幅。

参数:

• program (QProg) -- 要运行的量子程序。

• string (str) -- 二进制字符串。

返回:

指定二进制字符串的量子态振幅。

返回类型:

complex

抛出:

run_fail -- 获取振幅失败。

pmeasure_bin_subset(program: QProg, string_list: List[str]) → List[complex]

获取一组二进制字符串的量子态振幅。

参数:

• program (QProg) -- 要运行的量子程序。

• string_list (List[str]) -- 二进制字符串列表。

返回:

一组二进制字符串的量子态振幅。

返回类型:

List[complex]

抛出:

run_fail -- 获取振幅失败。

pmeasure_dec_index(program: QProg, string: str) → complex

获取指定十进制字符串的量子态振幅。

参数:

• program (QProg) -- 要运行的量子程序。

• string (str) -- 十进制字符串。

返回:

指定十进制字符串的量子态振幅。

返回类型:

complex

抛出:

run_fail -- 获取振幅失败。

pmeasure_dec_subset(program: QProg, string_list: List[str]) → List[complex]

获取一组十进制字符串的量子态振幅。

参数:

• program (QProg) -- 要运行的量子程序。

• string_list (List[str]) -- 十进制字符串列表。

返回:

一组十进制字符串的量子态振幅。

返回类型:

List[complex]

抛出:

run_fail -- 获取振幅失败。

prob_run_dict(program: QProg, qubit_list: QVec, select_max: int = -1) → Dict[str, float]

运行量子程序并获取测量概率结果的字典形式。

参数:

• program (QProg) -- 要运行的量子程序。

• qubit_list (QVec) -- 用于测量的量子比特列表。

• select_max (int, optional) -- 返回的元素数量上限。默认为 -1，表示无限制。

返回:

包含测量概率的字典，键为测量结果的二进制字符串，值为对应的测量概率。

返回类型:

Dict[str, float]

抛出:

run_fail -- 运行量子程序失败。

prob_run_list(program: QProg, qubit_list: QVec, select_max: int = -1) → List[float]

运行量子程序并获取测量概率结果的列表形式。

参数:

• program (QProg) -- 要运行的量子程序。

• qubit_list (QVec) -- 用于测量的量子比特列表。

• select_max (int, optional) -- 返回的元素数量上限。默认为 -1，表示无限制。

返回:

包含测量概率的列表。

返回类型:

List[float]

抛出:

run_fail -- 运行量子程序失败。

prob_run_tuple_list(program: QProg, qubit_list: QVec, select_max: int = -1) → List[Tuple[int, float]]

运行量子程序并获取测量概率结果的元组列表形式。

参数:

• program (QProg) -- 要运行的量子程序。

• qubit_list (QVec) -- 用于测量的量子比特列表。

• select_max (int, optional) -- 返回的元素数量上限。默认为 -1，表示无限制。

返回:

包含测量概率的元组列表，每个元组包含测量结果的索引和对应的概率。

返回类型:

List[Tuple[int, float]]

抛出:

run_fail -- 运行量子程序失败。

quick_measure(qubit_list: QVec, shots: int) → Dict[str, int]

快速进行多次测量。

参数:

• qubit_list (QVec) -- 用于测量的量子比特列表。

• shots (int) -- 测量操作的重复次数。

返回:

包含多次测量结果的字典，键为测量结果的二进制字符串，值为对应的出现次数。

返回类型:

Dict[str, int]

抛出:

run_fail -- 运行量子程序失败。

set_measure_error(noise_model: NoiseModel, error_rate: float, gate_type: GateType = GateType.HADAMARD_GATE, qubits: List[QVec] = []) → None

设置测量误差模型。

参数:

• noise_model (NoiseModel) -- 噪声模型。

• error_rate (float) -- 误差率。

• gate_type (GateType, optional) -- 误差应用的门类型。默认为 GateType.HADAMARD_GATE。

• qubits (List[QVec], optional) -- 用于应用误差的量子比特列表。默认为空列表。

返回:

无返回值。

set_mixed_unitary_error(gate_type: GateType, error_matrix: List[List[complex]], qubits: List[QVec] = []) → None

设置混合幺正误差模型。

参数:

• gate_type (GateType) -- 门类型。

• error_matrix (List[List[complex]]) -- 误差矩阵。

• qubits (List[QVec], optional) -- 用于应用误差的量子比特列表。默认为空列表。

返回:

无返回值。

set_noise_model(noise_model: NoiseModel, gate_type: GateType, error_rate: float, qubits: List[QVec] = []) → None

设置噪声模型。

参数:

• noise_model (NoiseModel) -- 噪声模型。

• gate_type (GateType) -- 误差应用的门类型。

• error_rate (float) -- 误差率。

• qubits (List[QVec], optional) -- 用于应用误差的量子比特列表。默认为空列表。

返回:

无返回值。

set_readout_error(readout_params: List[List[float]], qubits: QVec) → None

设置读数误差模型。

参数:

• readout_params (List[List[float]]) -- 读数误差参数列表。

• qubits (QVec) -- 用于应用误差的量子比特列表。

返回:

无返回值。

set_reset_error(reset_0_param: float, reset_1_param: float) → None

设置重置误差模型。

参数:

• reset_0_param (float) -- 重置到0态的参数。

• reset_1_param (float) -- 重置到1态的参数。

返回:

无返回值。

set_rotation_error(param: float) → None

设置旋转门误差模型。

参数:

param (float) -- 误差参数。

返回:

无返回值。

和许多其他模拟器的使用方法一样，都具有相同的量子虚拟机接口，比如下述简单的使用示例代码:

from numpy import pi
from pyqpanda import *

# 构建量子虚拟机
qvm = MPSQVM()

# 初始化操作
qvm.set_configure(64, 64)
qvm.init_qvm()

q = qvm.qAlloc_many(10)
c = qvm.cAlloc_many(10)

# 构建量子程序
prog = QProg()
prog << hadamard_circuit(q)\
    << CZ(q[2], q[4])\
    << CZ(q[3], q[7])\
    << CNOT(q[0], q[1])\
    << Measure(q[0], c[0])\
    << Measure(q[1], c[1])\
    << Measure(q[2], c[2])\
    << Measure(q[3], c[3])

# 量子程序运行100次，并返回测量结果
result = qvm.run_with_configuration(prog, c, 100)

# 打印量子态在量子程序多次运行结果中出现的次数
print(result)

qvm.finalize()

---

以下示例展示了张量网络模拟器计算部分接口的使用方式

from numpy import pi
from pyqpanda import *

qvm = MPSQVM()
qvm.set_configure(64, 64)
qvm.init_qvm()

q = qvm.qAlloc_many(10)
c = qvm.cAlloc_many(10)

prog = QProg()
prog << hadamard_circuit(q)\
    << CZ(q[2], q[4])\
    << CZ(q[3], q[7])\
    << CNOT(q[0], q[1])\
    << CZ(q[3], q[7])\
    << CZ(q[0], q[4])\
    << RY(q[7], pi / 2)\
    << RX(q[8], pi / 2)\
    << RX(q[9], pi / 2)\
    << CR(q[0], q[1], pi)\
    << CR(q[2], q[3], pi)\
    << RY(q[4], pi / 2)\
    << RZ(q[5], pi / 4)\
    << Measure(q[0], c[0])\
    << Measure(q[1], c[1])\
    << Measure(q[2], c[2])

# Monte Carlo采样模拟接口
result0 = qvm.run_with_configuration(prog, c, 100)

# 概率测量接口
result1 = qvm.prob_run_dict(prog, [q[0], q[1], q[2]], -1)

print(result0)
print(result1)

qvm.finalize()

上述代码中 run_with_configuration 与 prob_run_dict 接口分别用于Monte Carlo采样模拟和概率测量，他们分别输出模拟采样的结果和对应振幅的概率，上述程序的计算结果如下

# Monte Carlo 采样模拟结果
{'0000000000': 7,
 '0000000001': 12,
 '0000000010': 13,
 '0000000011': 10,
 '0000000100': 16,
 '0000000101': 14,
 '0000000110': 12,
 '0000000111': 16}

# 概率测量结果
{'000': 0.12499999999999194,
 '001': 0.12499999999999185,
 '010': 0.12499999999999194,
 '011': 0.124999999999992,
 '100': 0.12499999999999198,
 '101': 0.12499999999999194,
 '110': 0.12499999999999198,
 '111': 0.12499999999999208}

密度矩阵模拟器

目前量子计算机的主要局限在于通用量子计算机所需的量子系统规模非常大，技术实现困难，因而人们主要利用中小规模量子体系，解决特定问题。

对于纯态和混合态量子比特系统，需要找到一种在低比特情况下，正确模拟噪声测量以及对哈密顿算符期望进行求解，而 密度矩阵模拟器 提供这一问题的解决方案。

对于混合态，态矢已难以完整的表示系统的量子态，一般使用密度矩阵来描述：

\[\begin{aligned} \rho = \sum_{i}^{n} p_i|\varphi_i\rangle\langle\varphi_i| \end{aligned}\]

对于纯态，可简化为

\[\rho = |\varphi\rangle\langle\varphi|\]

回到前文所述的混合态，其密度矩阵为：

\[\begin{split}\rho = \frac{1}{2}|0\rangle\langle 0| + \frac{1}{2}|1\rangle\langle 1| = \frac{1}{2} \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix}\end{split}\]

而相同测量结果的 \(|\psi\rangle = \frac{1}{\sqrt 2}|0\rangle + \frac{1}{\sqrt 2}|1\rangle\) 纯态，其密度矩阵为：

\[\begin{split}\rho = |\psi\rangle\langle\psi| = \frac{1}{2} \begin{bmatrix} 1&1\\ 1&1 \end{bmatrix}\end{split}\]

由密度矩阵可见，两者的量子态是完全不同的。

对于纯态，有 \(tr(\rho^2) = 1\), 混合态 \(tr(\rho^2) < 1\)。\(tr(A)\) 表示求矩阵 \(A\) 的迹，即n维矩阵 \(A\) 中对角线上元素之和。

对于一般的酉矩阵逻辑门，用密度矩阵表示其对系统的态演化：

\[\rho^{\prime} = U{\rho}U^{\dagger}\]

使用密度矩阵表示测量结果，测量得到结果m的概率为：

\[p(m) = tr(M_{m}^{\dagger}M_m\rho)\]

上式中 \(M_m\) 叫做测量算子，通常也叫做投影算符。以我们的计算基 \(|0\rangle\) 为例，其投影到 \(|0\rangle\) 的投影算符为 \(|0\rangle\langle 0|\) , 因此，测量得到 \(|0\rangle\) 的概率为：

\[p(|0\rangle) = tr(|0\rangle\langle 0||0\rangle\langle 0|\rho)\]

以之前混合态和纯态的例子计算其测量结果为：

\[\begin{split}\begin{aligned} 混合态： p(|0\rangle) = tr( \frac{1}{2} \begin{bmatrix} 1&0\\ 0&0 \end{bmatrix} \begin{bmatrix} 1&0\\ 0&0 \end{bmatrix} \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix} ) =\frac{1}{2} \\ 纯态： p(|0\rangle) = tr( \frac{1}{2} \begin{bmatrix} 1&0\\ 0&0 \end{bmatrix} \begin{bmatrix} 1&0\\ 0&0 \end{bmatrix} \begin{bmatrix} 1&1\\ 1&1 \end{bmatrix} ) =\frac{1}{2} \\ \end{aligned}\end{split}\]

密度矩阵是表达量子态的另一种方式。而密度矩阵模拟器用于求解量子线路对应的密度矩阵，以及计算量子态概率分布、模拟含噪声量子线路和计算哈密顿量期望值等等。

---

pyqpanda 中可以通过 DensityMatrixSimulator 类实现用密度矩阵模拟器。和许多其他模拟器的使用方法一样，都具有相同的量子虚拟机接口:

class DensityMatrixSimulator(QuantumMachine)

该类是用于模拟密度矩阵的量子虚拟机。 该类提供了一系列方法用于模拟N比特的密度矩阵和约化密度矩阵的计算，以及直接获取不同噪声环境下量子线路模拟后的概率分布

get_density_matrix(prog: QProg) → numpy.ndarray[numpy.complex128[m, n]]

执行量子程序并获取完整的密度矩阵。

参数:

prog (QProg) -- 量子程序。

返回:

完整的密度矩阵。

返回类型:

numpy.ndarray[numpy.complex128[m,n]]

抛出:

run_fail -- 获取密度矩阵时发生错误。

get_expectation(prog: QProg, hamiltonian: List[Tuple[Dict[int, str], float]], qubits: QVec) → float

get_expectation(prog: QProg, hamiltonian: List[Tuple[Dict[int, str], float]], qubits: List[int]) → float

执行量子程序并计算给定哈密顿量的期望值。

参数:

• prog (QProg) -- 量子程序。

• hamiltonian (List[Tuple[Dict[int,str],float]]) -- 哈密顿量。

• qubits (QVec or List[int]) -- 选定的量子比特或量子比特列表。

返回:

选定量子比特上的哈密顿量期望值。

返回类型:

float

抛出:

run_fail -- 计算期望值时发生错误。

get_probabilities(prog: QProg) → List[float]

get_probabilities(prog: QProg, qubits: QVec) → List[float]

get_probabilities(prog: QProg, qubits: List[int]) → List[float]

get_probabilities(prog: QProg, indices: List[str]) → List[float]

执行量子程序并获取所有可能性的概率。

参数:

• prog (QProg) -- 量子程序。

• qubits (QVec or List[int]) -- 选定的量子比特或量子比特列表。

• indices (List[str]) -- 选定的二进制索引列表。

返回:

量子程序的概率结果。

返回类型:

List[float]

抛出:

run_fail -- 获取概率时发生错误。

get_probability(prog: QProg, index: int) → float

get_probability(prog: QProg, index: str) → float

执行量子程序并获取给定索引的概率。

参数:

• prog (QProg) -- 量子程序。

• index (int or str) -- 测量索引（在 [0,2^N - 1] 范围内）。

返回:

量子程序的概率结果。

返回类型:

float

抛出:

run_fail -- 获取概率时发生错误。

get_reduced_density_matrix(prog: QProg, qubits: QVec) → numpy.ndarray[numpy.complex128[m, n]]

get_reduced_density_matrix(prog: QProg, qubits: List[int]) → numpy.ndarray[numpy.complex128[m, n]]

执行量子程序并获取选定量子比特的约化密度矩阵。

参数:

• prog (QProg) -- 量子程序。

• qubits (QVec or List[int]) -- 选定的量子比特或量子比特列表。

返回:

约化密度矩阵。

返回类型:

numpy.ndarray[numpy.complex128[m,n]]

抛出:

run_fail -- 获取约化密度矩阵时发生错误。

init_qvm(is_double_precision: bool = True) → None

初始化量子虚拟机。

参数:

is_double_precision (bool, optional) -- 是否使用双精度（默认为 True）。

set_noise_model(arg0: numpy.ndarray[numpy.complex128[m, n]]) → None

set_noise_model(arg0: numpy.ndarray[numpy.complex128[m, n]], arg1: List[GateType]) → None

set_noise_model(arg0: List[numpy.ndarray[numpy.complex128[m, n]]]) → None

set_noise_model(arg0: List[numpy.ndarray[numpy.complex128[m, n]]], arg1: List[GateType]) → None

set_noise_model(arg0: NoiseModel, arg1: GateType, arg2: float) → None

set_noise_model(arg0: NoiseModel, arg1: List[GateType], arg2: float) → None

set_noise_model(arg0: NoiseModel, arg1: GateType, arg2: float, arg3: QVec) → None

set_noise_model(arg0: NoiseModel, arg1: List[GateType], arg2: float, arg3: QVec) → None

set_noise_model(arg0: NoiseModel, arg1: GateType, arg2: float, arg3: List[QVec]) → None

set_noise_model(arg0: NoiseModel, arg1: GateType, arg2: float, arg3: float, arg4: float) → None

set_noise_model(arg0: NoiseModel, arg1: List[GateType], arg2: float, arg3: float, arg4: float) → None

set_noise_model(arg0: NoiseModel, arg1: GateType, arg2: float, arg3: float, arg4: float, arg5: QVec) → None

set_noise_model(arg0: NoiseModel, arg1: List[GateType], arg2: float, arg3: float, arg4: float, arg5: QVec) → None

set_noise_model(arg0: NoiseModel, arg1: GateType, arg2: float, arg3: float, arg4: float, arg5: List[QVec]) → None

该方法用于设置噪声模型，以在模拟中引入量子门的错误。

参数:

• arg0 (numpy.ndarray[numpy.complex128[m,n]] or List[numpy.ndarray[numpy.complex128[m,n]]] or NoiseModel or GateType or float) -- 噪声模型参数，可能的类型包括 numpy 数组、噪声模型、量子门类型（GateType）、浮点数等。

• arg1 (Varies (See detailed descriptions)) -- 噪声模型的参数，具体类型取决于参数类型。

• arg2 (float) -- 噪声强度，表示引入的错误概率。

• arg3 (QVec or List[QVec] or QVec) -- 选定的量子比特列表（或量子比特），用于针对特定比特引入噪声（部分参数可能会用到）。

• arg4 (Varies (See detailed descriptions)) -- 更多参数，具体类型和用途取决于参数类型。

• arg5 (Varies (See detailed descriptions)) -- 更多参数，具体类型和用途取决于参数类型。

返回:

无返回值。

返回类型:

None

以下示例展示了密度矩阵模拟器计算部分接口的使用方式

from numpy import pi
from pyqpanda import *

machine = DensityMatrixSimulator()
machine.init_qvm()

q = machine.qAlloc_many(2)
c = machine.cAlloc_many(2)

prog = QProg()
prog.insert(H(q[0]))\
    .insert(Y(q[1]))\
    .insert(RY(q[0], pi / 3))\
    .insert(RX(q[1], pi / 6))\
    .insert(RX(q[1], pi / 9))\
    .insert(CZ(q[0], q[1]))

# 获取对应量子程序的密度矩阵
print(machine.get_density_matrix(prog))

# 获取对应量子程序的在指定量子比特下的约化密度矩阵
print(machine.get_reduced_density_matrix(prog, [0]))

# 获取对应量子程序指定量子态的概率
print("quantum state 00 probability : ", machine.get_probability(prog, "00"))

# 获取对应量子程序所有量子态的概率分布
print(machine.get_probabilities(prog))

# 获取对应量子程序指定哈密顿量下演化的期望值
operator = 0.23 * x(1) + 0.2 * y(1) + 1.6 * z(0)
expval = machine.get_expectation(prog,operator.to_hamiltonian(False),[0, 1])
print(expval)

# 设置噪声模型和参数
machine.set_noise_model(NoiseModel.BITFLIP_KRAUS_OPERATOR, GateType.HADAMARD_GATE, 0.3)
machine.set_noise_model(NoiseModel.BITFLIP_KRAUS_OPERATOR, GateType.CZ_GATE, 0.3)

# 获取加入噪声后，密度矩阵信息和概率分布
print(machine.get_density_matrix(prog))
print(machine.get_probabilities(prog))

machine.finalize()

输出结果如下：

# 对应量子程序的密度矩阵
[[ 0.01196435+0.j  0.04465155+0.j  0.-0.02565762j  1.+0.09575556j]
[ 0.04465155+0.j   0.16664185+0.j  0.-0.09575556j  1.+0.35736463j]
[ 0.+0.02565762j   0.+0.09575556j  0.05502295+0.j -0.20534845+0.j]
[-0.-0.09575556j  -0.-0.3573646j  -0.20534845+0.j  0.76637085-0.j]]

# 对应量子程序的在指定量子比特下的约化密度矩阵
[[ 0.0669873+0.j -0.1606969+0.j]
[-0.1606969+0.j  0.9330127+0.j]]

# 对应量子程序指定量子态的概率
quantum state 00 probability :  0.01196434643886035

# 对应量子程序所有量子态的概率分布
[0.01196434643886035, 0.1666418487178699, 0.05502295166892035, 0.7663708531743493]

# 对应量子程序指定哈密顿量下演化的期望值
-1.5183234356888893

# 加入噪声后，密度矩阵信息
[[ 0.12138551+0.j  -0.03034845+0.j  0.+0.03569962j 1.+0.03830222j]
[-0.03034845+0.j  0.25005696+0.j  0.-0.03830222j 1.+0.09698317j]
[ 0.-0.03569962j  0.+0.03830222j  0.2054094 +0.j -0.13034845+0.j]
[ 0.-0.03830222j  0.-0.09698317j -0.13034845+0.j 0.42314812+0.j]]

# 加入噪声后，概率分布
[0.12138551462195893, 0.25005696344073314, 0.20540940462115326, 0.4231481173161546]

除此之外，密度矩阵的噪声可以叠加，参考下面的一个简单的例子，对于如下的简单线路

from numpy import pi
from pyqpanda import *

machine = DensityMatrixSimulator()
machine.init_qvm()

prog = QProg()
q = machine.qAlloc_many(2)
c = machine.cAlloc_many(2)

prog.insert(X(q[0]))\
    .insert(CNOT(q[0], q[1]))

density_matrix1 = machine.get_density_matrix(prog)

print(density_matrix1)

当我们同时对所有X门设置触发两次比特翻转噪声时，密度矩阵的演化如下：

machine.set_noise_model(NoiseModel.BITFLIP_KRAUS_OPERATOR, GateType.PAULI_X_GATE, 0.3)
print(machine.get_density_matrix(prog))

machine.set_noise_model(NoiseModel.BITFLIP_KRAUS_OPERATOR, GateType.PAULI_X_GATE, 0.3)
print(machine.get_density_matrix(prog))

运行结果如下：

# 第一次施加的噪声
[[0.3+0.j 0. +0.j 0. +0.j 0. +0.j]
[0. +0.j 0. +0.j 0. +0.j 0. +0.j]
[0. +0.j 0. +0.j 0. +0.j 0. +0.j]
[0. +0.j 0. +0.j 0. +0.j 0.7+0.j]]

# 噪声再次叠加的结果
[[0.42+0.j 0. +0.j 0. +0.j 0. +0.j]
[0. +0.j 0. +0.j 0. +0.j 0. +0.j]
[0. +0.j 0. +0.j 0. +0.j 0. +0.j]
[0. +0.j 0. +0.j 0. +0.j 0.58+0.j]]

稳定器与Clifford模拟器

---

---

叠加和纠缠 都是量子优势的典型来源，但是当系统包含的量子比特个数N增加时，量子态系数的个数随N指数增加，将无法使用经典计算机实现传统的全振幅模拟，这一问题称为 指数墙问题 。

基于 Gottesman_knill定理 ，我们可以得知，在基于特定门集形成的稳定器线路中，我们是可以通过多项式复杂度进行模拟的，而这也意味着，可以在某些特定逻辑门构造的线路中打破量子的指数级加速霸权，将经典模拟应用到量子线路中，从而验证量子计算机的结果是否正确。并且在未来的容错量子计算机中，必然是需要冗余信息进行编码，从而达到容错计算的可能，这显然在基于目前量子计算模拟框架中是无法实现大比特线路的。

我们可以另辟蹊径，通过 stabilizer 及对应的 Clifford 门集模拟器可以有效利用其多项式模拟的特性，解决基于pauli噪声的容错量子计算。同时，为了推广到通用量子计算，也可以将stabilizer的理论性质带入到 Clifford+T 的模拟中，基于 Clifford+T 的模拟器，我们可以解决大比特下的non-clifford逻辑门较少前提下的量子模拟(Clifford+T可以近似分解任意逻辑门)。

---

对于一个量子态 \(|\psi\rangle\) （一般指纯态），如果存在一个酉矩阵U使得 \(U|\psi\rangle = |\psi\rangle\) ，那么称 \(|\psi\rangle\) 可以被U所stabilize，U是 \(|\psi\rangle\) 的一个stabilizer，比如 \(Z|0\rangle = |0\rangle\) 。

很明显，一个量子态存在多个stabilizer，当有多个stabilizer时，这些stabilizer的乘积自然也是stabilizer。

\(Z_{1}Z_{2}X_{1}X_{2}|\psi\rangle = Z_{1}Z_{2}|\psi\rangle = |\psi\rangle\)

这种乘法封闭性告诉我们stabilizer会形成一个 群 。

对于量子态 \(|\psi\rangle\) ，若幺正变换群S中的每个元素都是 \(|\psi\rangle\) 的stabilizer，则称整个幺正变换群S是 \(|\psi\rangle\) 的stabilizer group。

一般情况下我们只关注 \(P\text{auli}\) 矩阵 \(\left\{ X,Y,Z,I \right\}\) 作为stabilizer的情况，即 幺正变换群由Pauli群构成，即

\(Stab(|\psi\rangle) = \left\{ P \in \mathcal{P}_{n}:P|\psi\rangle = |\psi\rangle \right\}\)

上述式子中，Pauli群 \(\mathcal{P}_{n}\) 定义为作用在n比特上的 \(P\text{auli}\) 操作符的集合，其中相位系数为 \(\pm 1\) 和 \(\pm i\) 。

\(\mathcal{P}_{n} = \left\{ i^{\gamma}X(a)Z(b):\gamma \in \{ 0,1,2,3\},a,b \in \{ 0,1\}^{n} \right\}\)

该Pauli群中 \(P^{(1)},\ldots,P^{(m)} \in \mathcal{P}_{n}\) 各个元素均是独立的。那么我们依据Pauli群的特殊性质可以得到：

\(\begin{matrix} \text{Stab}(|00\rangle)\& = \left\{ I,Z_{1},Z_{2},Z_{1}Z_{2} \right\}\& = \left\langle Z_{1},Z_{2} \right\rangle \\ \text{Stab}(| + + \rangle)\& = \left\{ I,X_{1},X_{2},X_{1}X_{2} \right\}\& = \left\langle X_{1},X_{2} \right\rangle \\ \text{Stab}\left( \frac{\left| 00 \right\rangle + \left| 11 \right\rangle}{\sqrt{2}} \right)\& = \left\{ I,X_{1}X_{2},Z_{1}Z_{2}, - Y_{1}Y_{2} \right\}\& = \ \left\langle X_{1}X_{2},Z_{1}Z_{2} \right\rangle \\ \text{Stab}\left( \left| 0^{n} \right\rangle \right)\& = \left\{ Z(a):a \in \{ 0,1\}^{n} \right\}\& = \left\langle Z_{1},\ldots,Z_{n} \right\rangle \\ \end{matrix}\)

问题在于如何构造 Stabilizer Group ，这里就不得不提到，当 Cliffford Group 门集中的元素作用在Pauli群上会有这样一组变换:

\(\mathbf{P|\psi\rangle = |\psi\rangle \Longleftrightarrow}\left( \mathbf{\text{UP}}\mathbf{U}^{\mathbf{\dagger}} \right)\mathbf{U|\psi\rangle = U|\psi\rangle}\)

当我们将群写成形式 \(P = i^{\gamma}X(a)Z(b)\) ， Cliffford Group 的作用形式如下：

\(U_{j}PU_{j}^{\dagger} = i^{\gamma}X^{a_{1}}Z^{b_{1}} \otimes \ldots \otimes X^{a_{j - 1}}Z^{b_{j - 1}} \otimes UX^{a_{j}}Z^{b_{j}}U^{\dagger} \otimes X^{a_{j + 1}}Z^{b_{j + 1}} \otimes \ldots \otimes X^{a_{n}}Z^{b_{n}}\)

我们会惊讶的发现， \(\mathbf{U}_{\mathbf{j}}\mathbf{P}\mathbf{U}_{\mathbf{j}}^{\mathbf{\dagger}}\mathbf{=}\mathbf{P}_{\mathbf{\text{new}}}\) 。也就如下图所示：

这里可以发现，我们将 \(\mathcal{P}_{n}\) 中的Y的变换去除了，这是由于 \(Y = IXZ\) 。

\(|\psi\rangle \rightarrow U|\psi\rangle\)

等价的只需要追踪stabilizer的演化，同样可以得到系统完整的动力学信息。

\(S \rightarrow USU^{\dagger}\)

这里将量子态的逻辑门演化问题转化为更新量子态对应的 Stabilizer Group 问题，即使用 Stabilizer 模拟量子线路的核心思想是使用 Stabilizer Group 表征量子态，而不是传统模拟器的振幅。

也就是说，在基于特定门集形成的稳定器线路中，根据线路特性，通过多项式复杂度即可进行模拟超大数量的量子线路 （仅限由Clifford量子逻辑门集合和衍生集合组成：H, S, X, Y, Z, CNOT, CY, CZ, SWAP ）

---

pyqpanda 中可以通过 Stabilizer 类实现对大比特的Clifford线路模拟，和许多其他模拟器有类似的功能接口:

class Stabilizer(QuantumMachine)

基于Stablizer，模拟基本的Clifford量子线路的模拟器。

变量:

• _noise_model (NoiseModel) -- 噪声模型，用于模拟实际量子系统中的噪声。

• _noise_set (bool) -- 是否已设置噪声模型。

__init__()

构造函数，初始化 Stabilizer 类的实例。

init_qvm()

初始化Stablizer。

prob_run_dict(qprog: QProg, qubits: QVec, select_max: int = -1) → Dict[str, float]

运行量子程序并获取概率结果。

参数:

• qprog (QProg) -- 要运行的量子程序。

• qubits (QVec) -- 用于测量的量子比特。

• select_max (int, optional) -- 最大选择数（默认为 -1 表示不限制）。

返回:

量子程序的概率结果。

返回类型:

Dict[str, float]

run_with_configuration(qprog: QProg, shot: int) → Dict[str, int]

运行量子程序并获取测量结果。

参数:

• qprog (QProg) -- 要运行的量子程序。

• shot (int) -- 测量次数。

返回:

量子程序的测量结果。

返回类型:

Dict[str, int]

set_noise_model(noise_model: NoiseModel, gate_types: GateType | List[GateType], prob: float, target_qubits: QVec | List[QVec] | None = None) → None

设置噪声模型，用于模拟实际量子系统中的噪声。

参数:

• noise_model (NoiseModel) -- 噪声模型。

• gate_types (Union[GateType, List[GateType]]) -- 受噪声影响的门类型或门类型列表。

• prob (float) -- 噪声发生的概率。

• target_qubits (Optional[Union[QVec, List[QVec]]]) -- 受噪声影响的目标量子比特或目标量子比特列表（可选）。

返回:

无返回值。

返回类型:

None

此函数允许您设置用于模拟实际量子系统中噪声的噪声模型，以及受影响的门类型和概率。可以选择指定受影响的目标量子比特，目前支持的噪声模型如下：

• bit-flip ：比特翻转噪声模型，按指定概率发生X方向错误

• phase-flip ：相位翻转噪声模型，按指定概率发生Y方向错误

• bit-phase-flip ：比特相位翻转噪声模型，按指定概率发生Z方向错误

• phase-damping ：相位阻尼噪声模型，相位阻尼可转化为相位反转噪声模型

• depolarizing ：去极化噪声模型,X,Y和Z三个方向上发生等概率错误

---

from numpy import pi
from pyqpanda import *

# 初始化Clifford模拟器，默认最大支持6000比特
machine = Stabilizer()
machine.init_qvm()

q = machine.qAlloc_many(100)
c = machine.cAlloc_many(100)

# 构建量子线路，支持的门集为{ H, S, X, Y, Z, CNOT, CY, CZ, SWAP }
prog = QProg()
prog.insert(X(q[1]))\
    .insert(H(q[2]))\
    .insert(H(q[49]))\
    .insert(Z(q[2]))\
    .insert(CZ(q[0], q[22]))\
    .insert(CNOT(q[2], q[39]))\
    .insert(measure_all(q, c))\

# run_with_configuration用于获取测量操作的测量结果
result = machine.run_with_configuration(prog, 1000)
print(result)

machine.finalize()

输出结果如下：

{'000000000000000000000000000000000000000000000000000000000010': 254,
 '000000000000000000001000000000000000000000000000000000000110': 279,
 '000000000010000000000000000000000000000000000000000000000010': 251,
 '000000000010000000001000000000000000000000000000000000000110': 216}

---

from numpy import pi
from pyqpanda import *

# 初始化Clifford模拟器，默认最大支持6000比特
machine = Stabilizer()
machine.init_qvm()

q = machine.qAlloc_many(100)
c = machine.cAlloc_many(100)

# 构建量子线路，支持的门集为{ H, S, X, Y, Z, CNOT, CY, CZ, SWAP }
prog = QProg()
prog.insert(X(q[1]))\
    .insert(H(q[0]))\
    .insert(H(q[1]))\
    .insert(Z(q[99]))\
    .insert(CZ(q[0], q[22]))\
    .insert(CNOT(q[2], q[98]))\

# prob_run_dict用于获取指定比特的测量结果
result = machine.prob_run_dict(prog, [q[0],q[1],q[2]])
print(result)

machine.finalize()

输出结果如下：

{'000': 0.25, '001': 0.25, '010': 0.25, '011': 0.25, '100': 0.0, '101': 0.0, '110': 0.0, '111': 0.0}