量子相位估计

经典形式的量子相位估计QPE (Quantum Phase Estimation) 是在QFT的基础上构造的，QPE可以计算给定幺正算符U的特征值的相位，即求解 \(U\left|\psi\right\rangle= \ e^{2\pi i\varphi}\left|\psi\right\rangle\) 中的 \(\varphi\)，此处 \(\left|\psi\right\rangle\) 为U的特征向量。

QPE过程也可以表示为

\[\begin{aligned} {\rm QPE}({\rm U},|0\rangle_n|\psi\rangle_m)=|\tilde{\theta}\rangle_n|\psi\rangle_m. \end{aligned}\]

其中 \(\tilde{\theta}\) 为 \(2^n\theta\) 在二进制下的 \(n\) 位近似。

量子线路结构概览

假设已经构造好特征向量 \(\left|\psi\right\rangle\)，量子相位估计包含如下步骤：

1. 通过一系列特殊旋转量子门操作将U的特征值相位分解转移到辅助量子比特的振幅上；

2. 对辅助量子比特执行IQFT，将振幅上的特征值相位转移到基向量上；

3. 对辅助量子比特的基向量分别进行测量后综合可得到特征值的相位信息。

对于幺正算符 \(U\) 的一个特征量子态 \(\left|\psi\right\rangle\)，可以通过特定的量子门组合将该量子态对应的特征值相位提取到振幅，但量子态的振幅难以有效准确地测量。

必须借助其他量子门组合将特征值相位数据进行整合，最终通过IQFT可以由振幅到基向量进行数据转化的功能将特征值转移到基向量中。

备注

量子相位估计本质上是为了提取幺正算符的特征值相位，并以便于测量的形式输出。

量子线路构建

特征量子态与特征值相位提取

由特征量子态的定义有 \(U\left|\psi\right\rangle = e^{2\pi i\varphi}\left|\psi\right\rangle\)，于是由幺正算符 \(U\) 可以定义受控量子门 \((C-U)\) 使得

\[\begin{aligned} (C-U^{2^t})(a\left|0\right\rangle+b\left|1\right\rangle)\otimes\left|\psi\right\rangle \ =(a\left|0\right\rangle+e^{2\pi i\varphi2^t}b\left|1\right\rangle)\otimes\left|\psi\right\rangle. \end{aligned}\]

特征值相位 \(\varphi\) 通过这种受控变换可以提取到振幅中。

特征值相位由振幅转移到基向量

选取一组初始化为最大叠加态的辅助比特，通过受控量子门可以将特征值相位提取到振幅中：

\[(C-U^{2^0})\cdots(C-U^{2^n})\frac{1}{2^\frac{n}{2}}\otimes_{t=1}^n (\left|0\right\rangle+\left|1\right\rangle)= (\left|0\right\rangle+e^{2\pi i\varphi2^{1-1}}\ \left|1\right\rangle)\cdots(\left|0\right\rangle+e^{2\pi i\varphi2^{n-1}}\left|1\right\rangle).\]

此时辅助比特中的量子态形式与QFT的结果量子态相近，借助IQFT有如下结果：

\[\begin{split}\begin{aligned} & QFT^{-1}\frac{1}{2^\frac{n}{2}}\otimes_{t=1}^n(\left|0\right\rangle+e^{2\pi i\varphi2^{t-1}} \left|1\right\rangle) \\ & =QFT^{-1}\frac{1}{2^\frac{n}{2}}\Sigma_{k=0}^{2^n-1}e^{2\pi i \varphi k}\left|k\right\rangle \\ & =\frac{1}{2^n}\Sigma_{k=0}^{2^n-1}\Sigma_{x=0} ^{2^n-1}e^{-\frac{2\pi ik}{2^n}\left(x-2^n\varphi\right)}\left|x\right\rangle. \end{aligned}\end{split}\]

含特征值相位的基向量测量

对得到的结果量子态进行测量，结果可以分为两类：

1. 如果存在正整数 \(2^n\varphi\in \mathbb{Z}\)，则可以以概率 \(1\) 测量得到 \(\left|x\right\rangle=\left|2^n\varphi\right\rangle\)

2. 否则以至少概率 \(\frac{4}{\pi^2}\) 得到最接近 \(2^n\varphi\) 的整数，进而得到近似解

备注

如何从最接近 \(2^n\varphi\) 的整数反推得到 \(\varphi\) ？（提示：连续分数展开）

测量结果得到的是相位 \(\varphi\) 的近似解，近似解的精度与辅助比特的数目 \(n\) 相关。\(2^n\varphi\in \mathbb{Z}\) 的情况代表辅助比特的数目已经大于 \(\varphi\) 的二进制展开小数位数，因此才能得到精确解。

量子线路图与代码实现

QPE的量子线路图如下所示

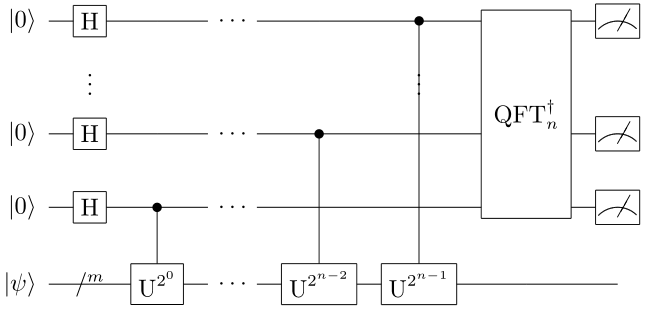
由上文中的定义，我们可以基于QPanda-2.0直接给出QPE的函数实现。

量子线路总共可以分为三个部分，特征量子态制备与辅助比特量子态初始化、特征值相位提取、逆量子傅里叶变换。程序实现的核心内容如下：

import pyqpanda as pq
from numpy import pi
import numpy as np

def QPE(controlqlist, targetqlist, matrix):
   circ = pq.QCircuit()
   for i in range(len(controlqlist)):
            circ.insert(pq.H(controlqlist[i]))

   for i in range(len(controlqlist)):
            circ.insert(pq.control_unitary_power(targetqlist, controlqlist[controlqlist.size() \
            - 1 - i], i, matrix))

   circ.insert(pq.QFT(controlqlist).dagger())
   return circ

图中的参数matrix是指需要估计特征值的幺正算符 \(U\) 对应的矩阵。

选取 \(U=RY(\frac{\pi}{4}),\left|\psi\right\rangle=\left|0\right\rangle+i\left|1\right\rangle\) ， 对应的特征值为 \(e^{-i\frac{\pi}{8}}\) ，验证QPE的代码实例如下

import pyqpanda as pq
from numpy import pi

if __name__ == "__main__":

   machine = pq.init_quantum_machine(pq.QMachineType.CPU)
   qvec = machine.qAlloc_many(1)
   cqv = machine.qAlloc_many(4)
   prog = pq.create_empty_qprog()

   # 构建量子程序
   prog.insert(pq.H(cqv[0]))\
       .insert(pq.H(cqv[1]))\
       .insert(pq.H(cqv[2]))\
       .insert(pq.H(cqv[3]))\
       .insert(pq.H(qvec[0]))\
       .insert(pq.S(qvec[0]))\
       .insert(pq.RY(qvec[0], pi/4).control(cqv[0]))\
       .insert(pq.RY(qvec[0], pi/2).control(cqv[1]))\
       .insert(pq.RY(qvec[0], pi).control(cqv[2]))\
       .insert(pq.RY(qvec[0], pi*2).control(cqv[3])) \
       .insert(pq.QFT(cqv).dagger())

   # 对量子程序进行概率测量
   result = pq.prob_run_dict(prog, cqv, -1)
   pq.destroy_quantum_machine(machine)

   # 打印测量结果
   for key in result:
       print(key+":"+str(result[key]))

由前文可知输出结果应当以接近 \(1\) 的概率得到量子态 \(\left|1111\right\rangle\) （即 \(-1\) ）

0000:8.027759204248868e-34
0001:1.4038818472306108e-33
0010:6.324302228415449e-35
0011:1.8002817275101533e-33
0100:1.1716099389234709e-34
0101:3.7184613996614186e-35
0110:7.14619905441006e-35
0111:3.163946664340403e-33
1000:1.1716099389234709e-34
1001:2.361635369532623e-33
1010:6.324302228415447e-35
1011:1.5092886417824937e-32
1100:2.0191804511467995e-34
1101:2.142003975785634e-33
1110:1.0410679182118513e-33
1111:0.999999999999936

量子傅里叶变换

量子傅里叶变换（QFT）实质上是经典的逆离散傅里叶变换（IDFT）的量子版本。

量子傅里叶变换可以将存在于基向量中的数据与振幅中的数据在一定条件下相互转换。

如图所示，QFT可以简单地通过对IDFT进行替换得到，QFT和DFT本质上都是同一个向量在两个等价空间中的不同表示形式，即基向量的更换。

\[\begin{split}\begin{aligned} y_k\rightarrow\frac{1}{\sqrt N}\Sigma_{j=0}^{N-1}x_j \ e^{\frac{2\pi\ i}{N}jk},\\ \left|x\right\rangle\rightarrow \ \frac{1}{2^\frac{n}{2}}\Sigma_{k=0}^{2^n-1}e^{\frac{2\pi i}{2^n} \ xk}\left|k\right\rangle. \end{aligned}\end{split}\]

由定义可知，空间 \(span\{\left|x\right\rangle\}\) 中的某个向量 \(\Sigma_x\alpha_x\left|x\right\rangle\) 通过傅里叶变换可以表示为另一个等价空间 \(span\{\left|k\right\rangle\}\) 中基向量的线性组合\(\Sigma_k\beta_k\left|k\right\rangle\), 且线性组合的系数 \(\beta_k\) 由\(\left|x\right\rangle\) 和 \(\alpha_x\) 决定。

备注

量子傅里叶变换/逆变换，实质上可以视为一种振幅和基向量的相互转化。

量子线路构造

对QFT的量子线路实现需要对其表达式进行变形，得到可以用现有普适量子门组合实现的变换过程。

对任给整数 \(x\) ，由二进制展开 \(k=\Sigma_{i=1}^nk_i2^{n-i}\)，对\(\left|x\right\rangle\) 进行量子傅里叶变换的结果可表示为

\[\begin{split}\begin{aligned} & QFT(\left|x\right\rangle)=\frac{1}{2^\frac{n}{2}}\Sigma_{k=0}^{2^n-1}e^\frac{2\pi ixk}{2^n} \ \left|k\right\rangle=\frac{1}{2^\frac{n}{2}}\Sigma_{k_1=0}^1\cdots\Sigma_{k_n=0}^1 \ e^{2\pi ixk\left(\Sigma_{l=1}^nk_l2^{-l}\right)}\left|k_1\cdots k_n\right\rangle \\ & =\frac{1}{2^\frac{n}{2}}\Sigma_{k_1=0}^1\cdots\Sigma_{k_n=0}^1\otimes_{l=1}^n e^{2\pi ix k_l2^{-l}} \left|k_l\right\rangle=\frac{1}{2^\frac{n}{2}}\otimes_{l=1}^n(\left|0\right\rangle+e^{2\pi ix2^{-l}} \ \left|1\right\rangle). \end{aligned}\end{split}\]

由上式可知，QFT可以将特定量子态 \(\left|x\right\rangle\) 表示为另一组基的线性组合，而这个线性组合还能表示为多个单比特量子态\(\frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi ix2^{-l}}\left|1\right\rangle)\) 的张量积。

因此对任给整数 \(x\)，如果可以由二进制展开位 \(\left|x_{n+1-l}\right\rangle\) 快速构造量子态 \(\frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi ix2^{-l}}\left|1\right\rangle)\)，那么就可以通过张量积形式的QFT表达式完成相应QFT量子线路的构造。

任给整数 \(x\) 进行二进制展开近似：

\[\begin{aligned} x/2^m \approx \left[x_1\cdots x_m\right]/2^m=\left[0.x_1\cdots x_m\right]=\Sigma_{k=1}^mx_k2^{-k}, \end{aligned}\]

而

\[\begin{aligned} 2\pi ix2^{-l}=2\pi i\left[x_1\cdots x_n\right]2^{-l}=2\pi i\left[0.x_{n-l}\cdots x_n\right]. \end{aligned}\]

于是制备 \(\frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi ix2^{-l}}\left|1\right\rangle)\) 转化为制备 \(\frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi i [0.x_{n-l}\cdots x_n]}\left|1\right\rangle)\) 。

注意到 \(H\left|0\right\rangle = \frac{1}{\sqrt{2}}(\left|0\right\rangle + \left|1\right\rangle) = \ \frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi i [0.x_n]}\left|1\right\rangle)\) ，而

\[\begin{split}\begin{aligned} & \frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi i [0.x_{n-1} x_n]}\left|1\right\rangle) = \ \frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi i [0.x_{n-1}]} e^{2\pi i [0.0 x_n]} \left|1\right\rangle),\\ & R_m \left|0\right\rangle = \left|0\right\rangle, R_m \left|1\right\rangle = e^{2\pi i \frac{1}{2^m}}\left|1\right\rangle. \end{aligned}\end{split}\]

定义受控旋转量子门 \((C-R)_{j-k+1}\) 满足

\[\begin{aligned} (C-R)_{j-k+1} \frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi i [0.x_{n-j}]} \left|1\right\rangle)\left|x_{n-k}\right\rangle = \frac{1}{\sqrt{2}}( \left|0\right\rangle + e^{2\pi i [0.x_{n-j}0\cdots 0x_{n-k}]}\left|1\right\rangle. \end{aligned}\]

于是利用量子门 \(H\) 和 \((C-R)_{j-k+1}\) 就可以完成对量子态\(\frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi ix2^{-l}}\left|1\right\rangle)\)的制备，进而完成QFT的量子线路。

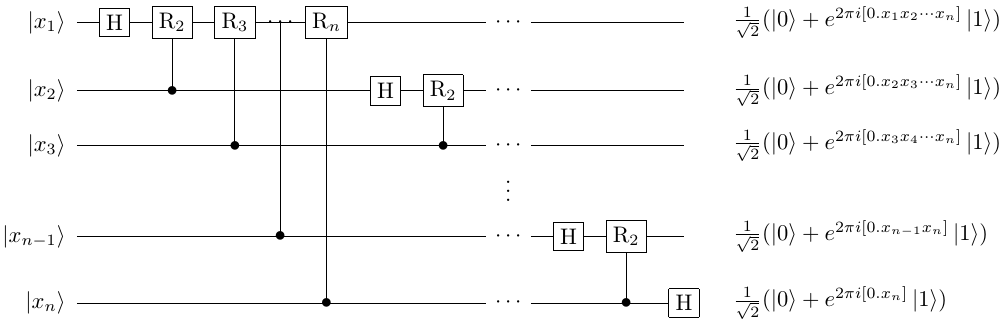
QFT的量子线路图如下所示

特别地，注意到上图中初始量子态为 \(\left|x_i\right\rangle\) 的量子比特对应的结果量子态为\(\frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi ix2^{n+1-l}}\left|1\right\rangle)\)而非 \(\frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi ix2^{-l}}\left|1\right\rangle)\) ，因此实际使用时还需要追加相应的多组 \(SWAP\) 门。

代码实现

QFT在一维情况就是Hadamard量子门。 基于QPanda-2.0的QFT接口函数如下：

QFT(qlist)

选取 \(\left|x\right\rangle=\left|000\right\rangle\) 验证QFT的代码实例如下

#!/usr/bin/env python

import pyqpanda as pq
from numpy import pi

if __name__ == "__main__":

    machine = pq.init_quantum_machine(pq.QMachineType.CPU)
    qvec = machine.qAlloc_many(3)
    prog = pq.create_empty_qprog()

    # 构建量子程序
    prog.insert(pq.QFT(qvec))

    # 对量子程序进行概率测量
    result = pq.prob_run_dict(prog, qvec, -1)
    pq.destroy_quantum_machine(machine)

    # 打印测量结果
    for key in result:
         print(key+":"+str(result[key]))

由前文中QFT的定义及 \(\left|x\right\rangle=\left|000\right\rangle\) 可知输出结果应当以均匀概率 \(\frac{1}{8}\) 得到所有量子态，即

000:0.125
001:0.125
010:0.125
011:0.125
100:0.125
101:0.125
110:0.125
111:0.125

优化算法(直接搜索法)

本章节将讲解优化算法的使用，包括 Nelder-Mead 算法跟 Powell 算法，它们都是一种直接搜索算法。我们在 QPanda 中实现了这两个算法，OriginNelderMead 和 OriginPowell ， 这两个类都继承自 AbstractOptimizer 。

我们可以通过优化器工厂生成指定类型的优化器，例如我们指定它的类型为Nelder-Mead

optimizer = OptimizerFactory.makeOptimizer(OptimizerType.NELDER_MEAD)
#optimizer = OptimizerFactory.makeOptimizer('Nelder-Mead')

我们需要向优化器注册一个计算损失值的函数和待优化参数。

init_para = [0, 0]
optimizer.registerFunc(lossFunc, init_para)

然后设置结束条件，我们可以设置变量及函数值的收敛阈值，函数最大可调用次数，和优化迭代次数。只要满足上述结束条件，则优化结束。

optimizer.setXatol(1e-6)
optimizer.setFatol(1e-6)
optimizer.setMaxFCalls(200)
optimizer.setMaxIter(200)

然后通过exec接口执行优化，通过getResult接口获得优化后的结果。

optimizer.exec()

result = optimizer.getResult()
print(result.message)
print(" Current function value: ", result.fun_val)
print(" Iterations: ", result.iters)
print(" Function evaluations: ", result.fcalls)
print(" Optimized para: W: ", result.para[0], " b: ", result.para[1])

给定一些散列点，我们来拟合一条直线，使得散列点到直线的距离和最小。定义直线的函数的表达式为 y = w*x + b ，接下来我们将通过使用优化算法得到w和b的优化值。 首先定义求期望的函数

from pyqpanda import *
import numpy as np

x = np.array([3.3, 4.4, 5.5, 6.71, 6.93, 4.168, 9.779, 6.182, 7.59,
             2.167, 7.042, 10.791, 5.313, 7.997, 5.654, 9.27,3.1])
y = np.array([1.7, 2.76, 2.09, 3.19, 1.694, 1.573, 3.366, 2.596, 2.53,
             1.221, 2.827, 3.465, 1.65, 2.904, 2.42, 2.94,1.3])

def lossFunc(para,grad,inter,fcall):
    y_ = np.zeros(len(y))

    for i in range(len(y)):
        y_[i] = para[0] * x[i] + para[1]

    loss = 0
    for i in range(len(y)):
        loss += (y_[i] - y[i])**2/len(y)

    return ("", loss)

我们使用 Nelder-Mead 算法进行优化

optimizer = OptimizerFactory.makeOptimizer('Nelder-Mead')

init_para = [0, 0]
optimizer.registerFunc(lossFunc, init_para)
optimizer.setXatol(1e-6)
optimizer.setFatol(1e-6)
optimizer.setMaxIter(200)
optimizer.exec()

result = optimizer.getResult()
print(result.message)
print(" Current function value: ", result.fun_val)
print(" Iterations: ", result.iters)
print(" Function evaluations: ", result.fcalls)
print(" Optimized para: W: ", result.para[0], " b: ", result.para[1])

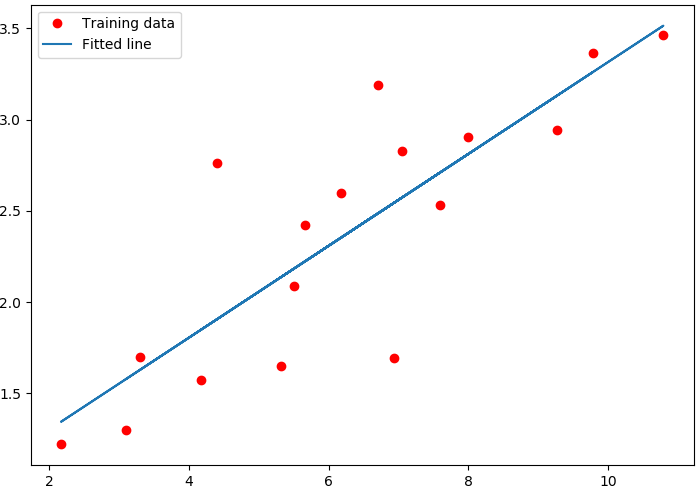
我们将散列点和拟合的直线进行绘图

import matplotlib.pyplot as plt

w = result.para[0]
b = result.para[1]

plt.plot(x, y, 'o', label = 'Training data')
plt.plot(x, w*x + b, 'r', label = 'Fitted line')
plt.legend()
plt.show()

哈密顿量模拟

哈密顿量以威廉·罗文·汉密尔顿（William Rowan Hamilton）命名，他也创造了牛顿力学的革命性改革，现在称为哈米尔顿力学，这在量子物理学中是重要的。 哈密顿量是所有粒子的动能的总和加上与系统相关的粒子的势能。 对于不同的情况或数量的粒子，哈密顿量是不同的，因为它包括粒子的动能之和以及对应于这种情况的势能函数。

在量子力学中，波函数 \(\Psi( |t \rangle)\) 的时间演化由含时薛定谔方程控制。

将普朗克常量视为1，将积分上下限分别定为 t、0，并经过一系列数学运算后，可以得到 \(\Psi( |t \rangle) = e^{-iHt} \Psi( |0 \rangle)\)

哈密顿量（哈密顿算符）在数学上被表示为Hermitian矩阵,而随着qubit数量的增加，其希尔伯特空间是指数增长的，相对应的哈密顿量的维度也是呈指数增长。 因此，需要使用一些近似方法，最简单的近似方法就是在关于矩阵的泰勒展开式 \(\Psi( |t \rangle) \approx (I-iHt) \Psi( |0 \rangle)\) 通过更高阶的近似，可以得到更高的精度逼近。

step1:构造相关矩阵；

step2:构造模拟线路；

step3:使用 QOperator 操作将线路构造成算符操作，并获取线路的对应矩阵；

step4:使用 expMat() 接口计算 e 的复数矩阵的真实值；

step5:使用 average_gate_fidelity() 接口计算两个矩阵的相似度。

import math
import numpy as np
import pyqpanda as pq

if __name__ == "__main__":
    pq.init(pq.QMachineType.CPU)
    q = pq.qAlloc_many(4)

    # 构建pauli 算子
    X = np.mat([[0, 1], [1, 0]])
    Y = np.mat([[0, -1j], [1j, 0]])
    Z = np.mat([[1, 0], [0, -1]])
    t = np.pi

    circuit_x = pq.create_empty_circuit()
    circuit_y = pq.create_empty_circuit()
    circuit_z = pq.create_empty_circuit()

    # 构造Hamiltonian Operator
    circuit_x << pq.H(q[0]) \
            << pq.X(q[0]) \
            << pq.RZ(q[0], -t) \
            << pq.X(q[0]) \
            << pq.RZ(q[0], t) \
            << pq.H(q[0])

    circuit_y << pq.RX(q[0], t / 2) \
            << pq.X(q[0]) \
            << pq.RZ(q[0], -t) \
            << pq.X(q[0]) \
            << pq.RZ(q[0], t) \
            << pq.RX(q[0], -t / 2)

    circuit_z << pq.X(q[0]) \
            << pq.RZ(q[0], -t) \
            << pq.X(q[0]) \
            << pq.RZ(q[0], t)

    operator_x = pq.QOperator(circuit_x)
    operator_y = pq.QOperator(circuit_y)
    operator_z = pq.QOperator(circuit_z)

    unitary_x = operator_x.get_matrix()
    unitary_y = operator_y.get_matrix()
    unitary_z = operator_z.get_matrix()

    conf = complex(0, -1)
    U_x = pq.expMat(conf, X, t)
    U_y = pq.expMat(conf, Y, t)
    U_z = pq.expMat(conf, Z, t)

    f_ave_x = pq.average_gate_fidelity(U_x, unitary_x)
    f_ave_y = pq.average_gate_fidelity(U_y, unitary_y)
    f_ave_z = pq.average_gate_fidelity(U_z, unitary_z)

    print("Pauli-X Average Gate Fidelity: F = {:f}".format(f_ave_x))
    print("Pauli-Y Average Gate Fidelity: F = {:f}".format(f_ave_y))
    print("Pauli-Z Average Gate Fidelity: F = {:f}".format(f_ave_z))

运行结果如下：

Pauli-X Average Gate Fidelity: F = 1.000000
Pauli-Y Average Gate Fidelity: F = 1.000000
Pauli-Z Average Gate Fidelity: F = 1.000000

振幅放大

振幅放大（Amplitude Amplification）线路的主要作用为对于给定纯态的振幅进行放大，从而调整其测量结果概率分布。

算法背景

假设某个实际问题转化而来的量子模型的解为 \(|\varphi_1\rangle\)，归一化的叠加态 \(|\psi\rangle\) 可由 \(|\varphi_1\rangle\) ，和它的正交量子态如下表示：\(|\psi\rangle=\sin\theta|\varphi_1\rangle+\cos\theta|\varphi_0\rangle\) 此处，\(|\varphi_0\rangle=|\varphi_1^\perp\rangle\) ，已知 \(|\psi\rangle\) 和 \(\theta\) ，求 \(|\varphi_1\rangle\) 利用振幅放大算法可以放大上述表达式中目标基向量 \(|\varphi_{1}\rangle\) 的系数，得到形如

\[\begin{aligned} |\psi_k\rangle=\sin{k\theta}|\varphi_1\rangle+\cos{k\theta}|\varphi_0\rangle,~k\theta\approx\frac{\pi}{2} \end{aligned}\]

的量子态，此时对 \(|\psi_k\rangle\) 测量得到问题解 \(|\varphi_{1}\rangle\) 的概率被放大到约为1，因此振幅放大量子线路又被称为提取线路。

考虑一个N维Hilbert空间，存在一个自共轭投影算符 \({\rm P}：{\rm H}\mapsto{\rm H}\) 使得

\[\begin{split}{\rm P}|x\rangle= \begin{cases} |x\rangle,~x\in {\rm H_0}\\ -|x\rangle,~x\in {\rm H_1} \end{cases}\end{split}\]

其中 \({\rm H}={\rm H_0}\oplus{\rm H_1}\)，要求出一个 \(x\in{\rm H_1}\).

首先构造出包含问题解的叠加态. 考虑N维量子态 \(|0\rangle_N\) ，由 \({\rm H}={\rm H_0}\oplus{\rm H_1}\) 可知存在一个不含测量的可逆量子算符 \(\mathcal{A}\) 使得

\[\begin{aligned} \mathcal{A}|0\rangle_N=|\psi\rangle=\cos\theta|\varphi_0\rangle+\sin\theta|\varphi_1\rangle \end{aligned}\]

其中 \(|\varphi_0\rangle=|\varphi_1^\perp\rangle,~\varphi_0\in{\rm H_0},~\varphi_1\in{\rm H_1}.\)

其次构造出能快速放大解 \(|\varphi_1\rangle\) 的系数的量子门. 定义幺正算符 \({\rm Q}=-({\rm I}-2|\psi\rangle\langle\psi|){\rm P}\)，则有

\[\begin{aligned} {\rm Q}|\varphi_0\rangle=-({\rm I}-2|\psi\rangle\langle\psi|)|\varphi_0\rangle=\cos{2\theta}|\varphi_0\rangle+\sin{2\theta}|\varphi_1\rangle \end{aligned}\]

\[\begin{aligned} {\rm Q}|\varphi_1\rangle=({\rm I}-2|\psi\rangle\langle\psi|)|\varphi_1\rangle=-\sin{2\theta}|\varphi_0\rangle+\cos{2\theta}|\varphi_1\rangle. \end{aligned}\]

于是在 \(\{|\varphi_0\rangle,~|\varphi_1\rangle\}张成的子空间{\rm H}_{\psi}内有{\rm Q}=\begin{bmatrix} \cos{2\theta} & -\sin{2\theta} \\ \sin{2\theta} & \cos{2\theta} \end{bmatrix}\).

Q门可视为角度为 \(2\theta\) 的旋转量子门操作. 实际上若记 \({\rm P}={\rm I}-2|\varphi_1\rangle\langle\varphi_1|\) ， Q门可视为对 \(|\varphi_0\rangle\) 和对 \(|\varphi_1\rangle\) 的镜像变换的组合。 \(|0\rangle_N\) 经过 \(\mathcal{A}\) 门和n次Q门旋转之后得到的量子态为

\[\begin{aligned} {\rm Q}^n|\psi\rangle=\cos{(2n+1)\theta}|\varphi_0\rangle+\sin{(2n+1)\theta}|\varphi_1\rangle. \end{aligned}\]

当选取 \(n=\lfloor\dfrac{\pi}{4\theta}\rfloor\) 时，测量量子态 \({\rm Q}^n|\psi\rangle\) 得到目标解 \(|\varphi_{1}\rangle\) 的概率 \(\sin^2{(2n+1)\theta}\) 趋于最大. 于是测量量子态 \({\rm Q}^n|\psi\rangle\) 能够以逼近 1 的概率得到问题的解.

进一步地，对振幅放大操作进行一般化推广，记

\[\begin{aligned} {\rm Q}=-\mathcal{A}S_{0}\mathcal{A}^{-1}S_{P} \end{aligned}\]

其中

\[\begin{split}\begin{aligned} S_{0}=\begin{cases} |x\rangle, ~x\in H_{0}\\ k|x\rangle, ~~x\in H_{1} \end{cases},~~ S_{P}=\begin{cases} kx, ~x=0\\ x, ~x\ne 0 \end{cases}. \end{aligned}\end{split}\]

则有

\[\begin{split}\begin{aligned} \begin{split} {\rm Q}|\varphi_0\rangle &=k(1+\cos^{2})(\theta)|\varphi_0\rangle+(1-k)\cos^{2}(\theta)|\varphi_1\rangle,\\ {\rm Q}|\varphi_1\rangle &=k(k-1)\sin^{2}(\theta)|\varphi_0\rangle+k((1-k)\sin^{2}(\theta)-1)|\varphi_1\rangle. \end{split} \end{aligned}\end{split}\]

证明的关键在于利用幺正算符 \(\mathcal{A}\) 性质得到

\[\begin{aligned} \langle \varphi|\varphi_{1}\rangle = \langle 0|\mathcal{A}^{\dagger}|\varphi_{1}\rangle= \langle 0|\mathcal{A}^{-1}|\varphi_{1}\rangle=\sin^{2}{\theta}. \end{aligned}\]

即

\[\begin{aligned} \mathcal{A}^{-1}|\varphi_{1}\rangle=\sin^{2}{\theta}|0\rangle+\lambda|1\rangle \end{aligned}\]

此处的 \({\rm Q}\) 为一般意义上的振幅放大算子，通过合理的选择 \(k\) ，可以得到不同的结果（比如更快的振幅放大）.

代码实例

取 \(\Omega=\{0,1\}, \left|\psi\right\rangle = \sin{\frac{\pi}{6}}\left|1\right\rangle+ \cos{\frac{\pi}{6}}\left|0\right\rangle,\ P_1=I-2\left|1\right\rangle \left\langle 1\right|=Z, P=I-2\left|\psi\right\rangle \left\langle\psi\right|\)，

振幅放大量子线路的相应代码实例如下

#!/usr/bin/env python

import pyqpanda as pq
from numpy import pi

if __name__ == "__main__":

    machine = pq.init_quantum_machine(pq.QMachineType.CPU)
    qvec = machine.qAlloc_many(1)
    prog = pq.create_empty_qprog()

    # 构建量子程序
    prog.insert(pq.RY(qvec[0], pi/3))
    prog.insert(pq.Z(qvec[0]))
    prog.insert(pq.RY(qvec[0], pi*4/3))

    # 对量子程序进行概率测量
    result = pq.prob_run_dict(prog, qvec, -1)
    pq.destroy_quantum_machine(machine)

    # 打印测量结果
    for key in result:
         print(key+":"+str(result[key]))

输出结果应如下所示，分别以 \(1\) 和 \(0\) 的概率得到 \(\left|1\right\rangle\)和 \(\left|0\right\rangle\) ：

0:0
1:1

试验态制备与量子纠缠

试验态制备

试验态制备，指的是量子计算中任意算法的初始量子态的构造，是量子计算的初始步骤。

以单比特的两态空间为例，在实际量子运算中，我们可以直接得到的默认量子态是基态 \(\left|0\right\rangle\)，通过非门可以间接得到基态 \(\left|1\right\rangle\)。

对于任给的目标叠加量子态，我们则需要构造相应的量子门组合来得到。从基态 \(\left|0\right\rangle\) 出发制备任给目标叠加态的过程称为初态制备。

最大叠加态

以二比特态空间为例，从 \(\left|0\right\rangle^{\otimes2}\) 出发，对每个量子比特进行Hadamard门操作可以得到二比特空间中所有基态的均匀叠加。

类似地，在任意维态空间中，均可以借助Hadamard门从多维的 \(\left|0\right\rangle\) 基态出发，得到所有基态均匀线性组合的量子态。

这种量子态称为最大叠加态，很多量子计算中量子比特的初始状态要求为最大叠加态，量子计算的并行性也有赖于此。

通过试验态制备，我们就可以得到任意的基础量子态，从而完成量子计算中运算对象的构造。但是在执行运算操作之前，我们需要对量子计算所使用的量子比特给出明确的约束——纠缠关联。

在介绍量子纠缠之前，我们需要介绍一下纯态和混态。

纯态与混态的区分方式有多种，典型的有布洛赫球（Bloch Sphere），将态空间与Bloch球关联，球面上量子态为纯态，球体内的量子态为混态。

另一种重要的区分方式为密度矩阵，混态的密度矩阵的平方的迹小于1。

量子纠缠

如果一个量子系统的量子态 \(\left|\psi\right\rangle\) 可以表示成形如 \(\left|\psi\right\rangle=\left|\psi_0\ \right\rangle\otimes\left|\psi_1\right\rangle\) 的两个量子系统的直积形式，我们就将此量子态称为直积态。

备注

不能进行这种直积分解的量子态就是纠缠态。

例如对二比特的Bell态 \(\frac{1}{\sqrt2}\left|00\right\rangle+\frac{1}{\sqrt2}\left|11\right\rangle\)，它不能写成两个单比特量子态的直积形式。

量子纠缠态有超越经典关联的量子关联。为了发挥量子计算的并行性和高效性，量子计算使用的量子比特之间应当有着纠缠关联。

最大叠加态制备

下面是基于QPanda-2.0的最大叠加态制备的代码实现，调用的量子比特之间有着纠缠关联。

#!/usr/bin/env python

import pyqpanda as pq

if __name__ == "__main__":

    machine = pq.CPUQVM()
    machine.init_qvm()
    qubits = machine.qAlloc_many(3)
    prog = pq.QProg()

    # 构建量子程序
    prog.insert(pq.H(qubits[0])) \
        .insert(pq.H(qubits[1])) \
        .insert(pq.H(qubits[2]))

    # 对量子程序进行概率测量
    result = machine.prob_run_dict(prog, qubits, -1)

    # 打印测量结果
    for key in result:
        print(key+":"+str(result[key]))

运行结果应当是以均匀概率1/8得到3比特空间中所有量子态：

000:0.125
001:0.125
010:0.125
011:0.125
100:0.125
101:0.125
110:0.125
111:0.125

量子态编码

量子态编码是一个将经典信息转化为量子态的过程。在使用量子算法解决经典问题的过程中，量子态编码是非常重要的一步。比如在使用HHL算法解如下线性方程组时

\[\begin{split}\begin{aligned} A=\left(\begin{array}{cc} 1 & -1 / 3 \\ -1 / 3 & 1 \end{array}\right), \vec{x}=\left(\begin{array}{l} x_{1} \\ x_{2} \end{array}\right), \vec{b}=\left(\begin{array}{l} 1 \\ 0 \end{array}\right) \end{aligned}\end{split}\]

需要将向量b编码至线路中。而大多数量子态编码都是以 \(\left|0\right\rangle\) 为基态进行制备，而制备后的经典信息则可以表现在量子线路的各个参数中。 本教程中我们将讨论四种量子编码的方式，包括基态编码、角度编码、振幅编码、IQP 编码。在pyqpanda中，我们内置了这四类量子编码方式至 Encode 类中。

class Encode

Encode类提供了多种量子态编码方法，用于将量子态编码为不同格式的函数，其中包括编码为二进制串的基态编码，编码至角度及相位的角度编码，以及针对稀疏数据、密集数据的多种振幅编码方式，以及近似振幅编码方法。

basic_encode(qubit, data)

基态编码[1]是将一个 \(n\) 位的二进制字符串 \(x\) 转换为一个具有 \(n\) 个量子比特的系统的量子态 \(\left|x\right\rangle=\left|\psi\right\rangle\) 其中， \(\left|\psi\right\rangle\) 为转换后的计算基态。 例如，当需要对一个长度为4的二进制字符串 \(1001\) 编码时，得到的结果即为 \(\left|1001\right\rangle\) 。

参数:

• qubit (QVec) -- 编码比特列表。

• data (str) -- 编码数据。

返回:

None

返回类型:

None

示例:

from pyqpanda import *
import numpy as np

if __name__=="__main__":

    #构建全振幅虚拟机
    qvm = CPUQVM()
    qvm.init_qvm()

    x = '1001'

    #申请量子比特
    qubits = qvm.qAlloc_many(4)

    #实例化编码类Encode
    cir_encode=Encode()

    #调用Encode类中基态编码接口
    cir_encode.basic_encode(qubits,x)

    #调用Encode类中内置获取编码线路接口
    prog = QProg()
    prog << cir_encode.get_circuit()

    #获取量子编码后的编码比特
    encode_qubits = cir_encode.get_out_qubits()

    #获取线路的概率测量结果
    result = qvm.prob_run_dict(prog, encode_qubits)

    print(result)

{'0000': 0.0, '0001': 0.0, '0010': 0.0, '0011': 0.0, '0100': 0.0, '0101': 0.0, '0110': 0.0, '0111': 0.0, '1000': 0.0, '1001': 1.0, '1010': 0.0, '1011': 0.0, '1100': 0.0, '1101': 0.0, '1110': 0.0, '1111': 0.0}

angle_encode(qubit, data, gate_type = GateType::RY_GATE)

角度编码[1]即是利用旋转门 \(R_{x}\) , \(R_{y}\) , \(R_{z}\) 的旋转角度进行对经典信息的编码。

\[\begin{aligned} |\boldsymbol{x}\rangle=\bigotimes_{i=1}^{N} \cos \left(x_{i}\right)|0\rangle+\sin \left(x_{i}\right)|1\rangle \end{aligned}\]

其中 \(\left|x\right\rangle\) 即为所需编码的经典数据向量。

参数:

• qubit (QVec) -- 编码比特列表。

• data (List[float]) -- 编码数据。

Parm gate_type:

编码的泡利旋转门类型，默认为 RY_GATE

返回:

None

返回类型:

None

示例:

下面我们以 \(R_{y}\) 门编码一组角度 \([\pi,\pi]\) 为例

from pyqpanda import *
import numpy as np

if __name__=="__main__":

    #构建全振幅虚拟机
    qvm = CPUQVM()
    qvm.init_qvm()
    x = [np.pi,np.pi]

    #申请量子比特
    qubits = qvm.qAlloc_many(2)

    #实例化编码类Encode
    cir_encode = Encode()

    #调用Encode类中经典角度编码或密集角度编码接口并输出概率
    cir_encode.angle_encode(qubits,x)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits=cir_encode.get_out_qubits()
    result = qvm.prob_run_dict(prog, encode_qubits)
    print(result)
    qvm.finalize()

{'00': 1.405799628556214e-65, '01': 3.749399456654644e-33, '10': 3.749399456654644e-33, '11': 1.0}

dense_angle_encode(qubit, data)

由于一个qubit不仅可以加载角度信息，还可以加载相位信息，因此，我们完全可以将一个长度为N的经典数据编码至 \(\lceil N \rceil\) 个量子比特上。

\[\begin{aligned} |\boldsymbol{x}\rangle=\bigotimes_{i=1}^{\lceil N / 2\rceil} \cos \left(\pi x_{2 i-1}\right)|0\rangle+e^{2 \pi i x_{2 i}} \sin \left(\pi x_{2 i-1}\right)|1\rangle \end{aligned}\]

其中，将两个数据分别编码至量子特的旋转角度 \(\cos \left(\pi x_{2 i-1}\right)|0\rangle\) 与相位信息中 \(e^{2 \pi i x_{2 i}} \sin \left(\pi x_{2 i-1}\right)|1\rangle\)。

参数:

• qubit (QVec) -- 编码比特列表。

• data (List[float]) -- 编码数据。

返回:

None

返回类型:

None

可以发现，在经典角度编码中将经典数据向量 \(x\) 向 \(y\) 轴旋转了 \(\pi\)。由于密集角度编码会将一半信息编码至量子态的相位信息中。那么，我们可以调用 pyqpanda 的 qvm.directly_run 接口，获取系统的量子态信息，

from pyqpanda import *
import numpy as np

if __name__=="__main__":

    #构建全振幅虚拟机
    qvm = CPUQVM()
    qvm.init_qvm()
    x = [np.pi,np.pi]
    x = np.asarray(x)
    #实例化编码类Encode
    cir_encode = Encode()

    #申请量子比特
    qubits = qvm.qAlloc_many(1)
    cir_encode.dense_angle_encode(qubits,x)
    prog = QProg()
    prog << cir_encode.get_circuit()
    qvm.directly_run(prog)
    result = qvm.get_qstate()
    print(result)
    qvm.finalize()

[(6.123233995736766e-17+0j), (-1+1.2246467991473532e-16j)]

振幅编码即是将一个长度为 \(N\) 的数据向量 \(x\) 编码至数量为 \(\lceil log_{2}N \rceil\) 的量子比特的振幅上，具体公式如下：

\[\begin{aligned} \left|\psi\right\rangle=x_{0}|0\rangle+\cdots+x_{N-1}|N-1\rangle \end{aligned}\]

然而，可以发现由于处于纯态或混合态的量子系统的迹是为1的，所以我们需要将数据进行归一化处理，因此在接口入参时会进行校验。 同时，一个编码算法需要考虑的通常有三点，分别为编码线路的深度，宽度(qubit数量)，以及CNOT门的数量。因此，对应以上三点，在pyqpanda中也提供了不同的编码方法。同时根据数据形式的不同也可分为密集数据编码和稀疏数据编码。

amplitude_encode(qubit, data)

Top-down[2]的编码方式，顾名思义，即是将数据向量先进行处理，得到对应的角度树，并从角度树的根节点开始，依次向下进行编码，如下图所示：

参数:

• qubit (QVec) -- 编码比特列表。

• data (List[float] 或 List[complex]) -- 编码数据。

返回:

None

返回类型:

None

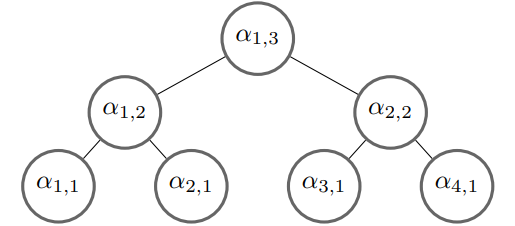
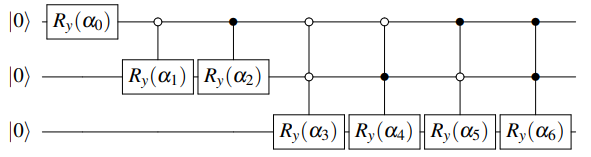
这种编码方式具有 \(O(\lceil log_{2} N \rceil)\) 的线路宽度，以及 \(O(n)\) 的线路深度。

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine=CPUQVM()
    machine.init_qvm()

    data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
    data = np.asarray(data)
    qubit = machine.qAlloc_many(3)
    cir_encode = Encode()
    cir_encode.amplitude_encode(qubit,data)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

                                                               ┌────────────┐     ┌────────────┐     >
q_0:  |0>─────────────── ────────────── ─── ────────────── ─── ┤RY(0.000000)├ ─── ┤RY(3.141593)├ ─── >
                         ┌────────────┐     ┌────────────┐     └──────┬─────┘ ┌─┐ └──────┬─────┘ ┌─┐ >
q_1:  |0>─────────────── ┤RY(1.570796)├ ─── ┤RY(0.000000)├ ─── ───────■────── ┤X├ ───────■────── ┤X├ >
          ┌────────────┐ └──────┬─────┘ ┌─┐ └──────┬─────┘ ┌─┐        │       └─┘        │       ├─┤ >
q_2:  |0>─┤RY(1.910633)├ ───────■────── ┤X├ ───────■────── ┤X├ ───────■────── ─── ───────■────── ┤X├ >
          └────────────┘                └─┘                └─┘                                   └─┘ >

         ┌────────────┐     ┌────────────┐
q_0:  |0>┤RY(0.000000)├ ─── ┤RY(3.141593)├ ───
         └──────┬─────┘ ┌─┐ └──────┬─────┘ ┌─┐
q_1:  |0>───────■────── ┤X├ ───────■────── ┤X├
                │       └─┘        │       ├─┤
q_2:  |0>───────■────── ─── ───────■────── ┤X├
                                           └─┘

{'000': 1.2497998188848808e-33, '001': 0.33333333333333315, '010': 0.0, '011': 0.0, '100': 1.2497998188848817e-33, '101': 0.3333333333333334, '110': 0.3333333333333334, '111': 0.0}

dc_amplitude_encode(qubit, data)

与Top-down编码方式相反，Bottom-top[2]通过 \(O(n)\) 的宽度构建一个 \(O(\lceil log_{2} N \rceil)\) 深度的量子线路。 其中，角度树中最左子树( \(\alpha_{0}\) , \(\alpha_{1}\) , \(\alpha_{3}\) )对应的量子比特为输出比特，其余为辅助比特。构建形式如下图所示：

参数:

• qubit (QVec) -- 编码比特列表。

• data (List[float]) -- 编码数据。

返回:

None

返回类型:

None

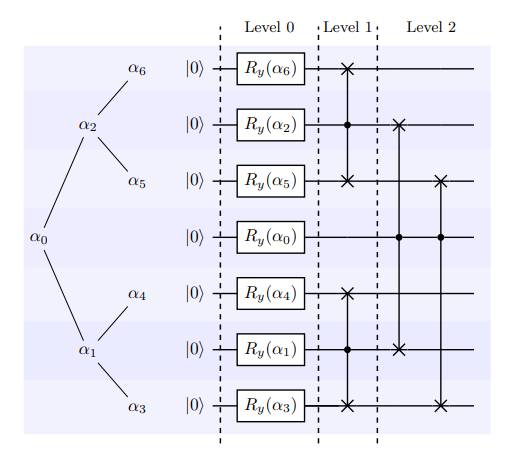
其中，level1，与level2对应的量子逻辑门为受控SWAP门，其作用为交换辅助比特与输出比特量子态。

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine = CPUQVM()
    machine.init_qvm()

    data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
    data = np.asarray(data)
    qubit = machine.qAlloc_many(7)
    cir_encode = Encode()
    cir_encode.dc_amplitude_encode(qubit,data)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

          ┌────────────┐
q_0:  |0>─┤RY(1.910633)├ ─── ■─ ■─
          ├────────────┤     │  │
q_1:  |0>─┤RY(0.000000)├ ■── X─ ┼─
          ├────────────┤ │   │  │
q_2:  |0>─┤RY(1.570796)├ ┼■─ X─ ┼─
          ├────────────┤ ││     │
q_3:  |0>─┤RY(3.141593)├ X┼─ ── X─
          ├────────────┤ ││     │
q_4:  |0>─┤RY(0.000000)├ X┼─ ── ┼─
          ├────────────┤  │     │
q_5:  |0>─┤RY(3.141593)├ ─X─ ── X─
          ├────────────┤  │
q_6:  |0>─┤RY(0.000000)├ ─X─ ── ──
          └────────────┘


{'000': 1.2497998188848807e-33, '001': 0.33333333333333315, '010': 0.0, '011': 0.0, '100': 1.2497998188848817e-33, '101': 0.3333333333333334, '110': 0.3333333333333334, '111': 0.0}

bid_amplitude_encode(qubit, data, spilt)

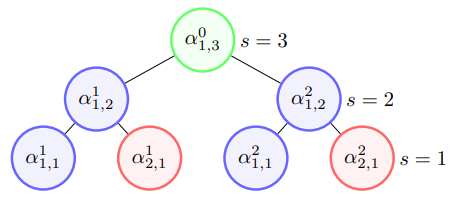
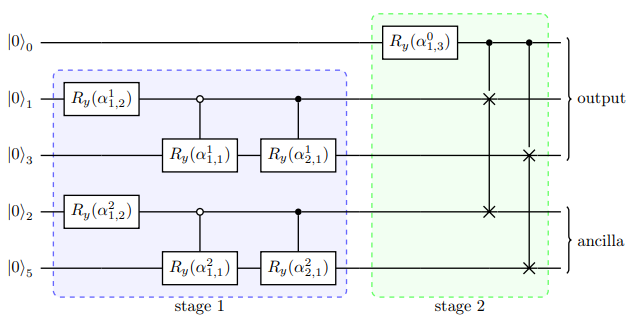
双向振幅编码[2]则是综合了Top-down和Bottom-top两种编码方式，即可通过参数 \(split\) 控制决定其线路深度与宽度。 其线路宽度为 \(O_{w}\left(2^{split}+\log _{2}^{2}(N)-split^{2}\right)\) ，线路深度为 \(O_{d}\left((split+1) \frac{N}{2^{split}}\right)\) ，而在我们pyqpanda中的接口默认为 \(n/2\)。 从 \(O_{w}\) 和 \(O_{d}\) 的公式可以看出当split为1时，则为Bottom-top振幅编码，当spilt为n时则为Top-down振幅编码。

参数:

• qubit (QVec) -- 编码比特列表。

• data (List[float]) -- 编码数据。

• spilt (int) -- 量子线路深度与宽度调节因子，其宽度表达式为 \(O_{w}\left(2^{split}+\log _{2}^{2}(N)-split^{2}\right)\) ，深度表达式为 \(O_{d}\left((split+1) \frac{N}{2^{split}}\right)\)，默认值为 \(N/2\)

返回:

None

返回类型:

None

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine=CPUQVM()
    machine.init_qvm()

    data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
    qubit = machine.qAlloc_many(5)
    data = np.asarray(data)
    cir_encode = Encode()
    cir_encode.bid_amplitude_encode(qubit,data)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

          ┌────────────┐
q_0:  |0>─┤RY(1.910633)├ ────────────── ─── ────────────── ─── ■─ ■─
          ├────────────┤                ┌─┐                ┌─┐ │  │
q_1:  |0>─┤RY(0.000000)├ ───────■────── ┤X├ ───────■────── ┤X├ X─ ┼─
          └────────────┘ ┌──────┴─────┐ └─┘ ┌──────┴─────┐ └─┘ │  │
q_2:  |0>─────────────── ┤RY(0.000000)├ ─── ┤RY(3.141593)├ ─── ┼─ X─
          ┌────────────┐ └────────────┘ ┌─┐ └────────────┘ ┌─┐ │  │
q_3:  |0>─┤RY(1.570796)├ ───────■────── ┤X├ ───────■────── ┤X├ X─ ┼─
          └────────────┘ ┌──────┴─────┐ └─┘ ┌──────┴─────┐ └─┘    │
q_4:  |0>─────────────── ┤RY(0.000000)├ ─── ┤RY(3.141593)├ ─── ── X─
                         └────────────┘     └────────────┘


{'000': 1.2497998188848807e-33, '001': 0.33333333333333315, '010': 0.0, '011': 0.0, '100': 1.2497998188848813e-33, '101': 0.3333333333333334, '110': 0.3333333333333334, '111': 0.0}

schmidt_encode(qubit, data, cutoff)

如Top-down振幅编码所示，使用 \(\lceil log_{2} N \rceil\) 个量子比特编码长度为 ：\(N\) 的经典数据大约需要 \(2^{2n}\) 个受控旋转门，这极大的降低了量子线路的 保真度，然而基于schmidt分解振幅编码[3]可以有效降低线路中的受控旋转门数量。首先，一个纯态 \(|\psi\rangle\) 可以被表示为如下形式：

\[\begin{aligned} |\psi\rangle=\sum_{i=1}^{k} \lambda_{i}\left|\alpha_{i}\right\rangle \otimes\left|\beta_{i}\right\rangle \end{aligned}\]

进一步，可以表示为：

\[\begin{aligned} |\psi\rangle=\sum_{i=1}^{m} \sum_{j=1}^{n} C_{i j}\left|e_{i}\right\rangle \otimes\left|f_{j}\right\rangle \end{aligned}\]

其中，\(\left|e_{i}\right\rangle \in \mathbb{C}^{m},\left|f_{j}\right\rangle \in \mathbb{C}^{n}\)。而 \(C\) 可以进行奇异值分解(svd) \(C=U \Sigma V^{\dagger}\), 通过以上公式，我们可以得出 \(\sigma_{i i}=\lambda_{i}\) ， \(\left|\alpha_{i}\right\rangle=U\left|e_{i}\right\rangle\) ， \(\left|\beta_{i}\right\rangle=V^{\dagger}\left|f_{i}\right\rangle\), 其中，\(\sigma_{i i}\) 则是 \(C\) 的奇异值。线路图构建如下：

参数:

• qubit (QVec) -- 编码比特列表。

• data (List[float]) -- 编码数据。

• cutoff (double) -- 表示奇异值向量的截断系数，范围为[0,1)，0表示不截断。

返回:

None

返回类型:

None

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine=CPUQVM()
    machine.init_qvm()

    data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
    data = np.asarray(data)
    qubit = machine.qAlloc_many(3)
    cir_encode = Encode()
    cir_encode.schmidt_encode(qubit,data,0)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

                         ┌────┐              ┌────────────┐  ┌─────────────┐ ┌─────────────┐ ┌────────────┐ >
q_0:  |0>─────────────── ┤CNOT├───────────── ┤RZ(3.141593)├─ ┤RY(-2.588018)├ ┤RZ(-3.141593)├ ┤RX(1.570796)├ >
          ┌────────────┐ └──┬┬┴────────────┐ ├────────────┤  └─────────────┘ └─────────────┘ └────────────┘ >
q_1:  |0>─┤RZ(4.712389)├ ───┼┤RY(-1.570796)├ ┤RZ(1.570796)├─ ─────────────── ─────────────── ────────────── >
          ├────────────┤    │└─────────────┘ ├────────────┴┐ ┌─────────────┐                                >
q_2:  |0>─┤RY(0.729728)├ ───■─────────────── ┤RY(-2.034444)├ ┤RZ(-3.141593)├ ─────────────── ────────────── >
          └────────────┘                     └─────────────┘ └─────────────┘                                >

                ┌─────────────┐        ┌─────────────┐ ┌─────────────┐ ┌─────────────┐ ┌────────────┐ ┌─────────────┐
q_0:  |0>───■── ┤RX(-1.570796)├ ───■── ┤RX(-1.570796)├ ┤RY(-1.570796)├ ┤RZ(-1.570796)├ ┤U1(4.712389)├ ┤RZ(-4.712389)├
         ┌──┴─┐ ├─────────────┤ ┌──┴─┐ ├─────────────┤ └─────────────┘ └─────────────┘ └────────────┘ └─────────────┘
q_1:  |0>┤CNOT├ ┤RY(-1.017222)├ ┤CNOT├ ┤RY(-3.141593)├ ─────────────── ─────────────── ────────────── ───────────────
         └────┘ └─────────────┘ └────┘ └─────────────┘
q_2:  |0>────── ─────────────── ────── ─────────────── ─────────────── ─────────────── ────────────── ───────────────



{'000': 1.4442161374080831e-64, '001': 0.3333333333333333, '010': 3.8518598887744744e-32, '011': 1.2497998188848808e-33, '100': 1.2497998188848825e-33, '101': 0.3333333333333337, '110': 0.3333333333333337, '111': 1.2497998188848825e-33}

approx_mps(qubit, data, layers=3, sweeps=100, double2float=False)

MPS近似编码[4]是一种利用矩阵乘积态的低秩表达近似分布制备算法，可以通过一种较少的CNOT的门完成对分布的表达， 并且这种表达是一种近邻接形式，因此可以直接作用于芯片，且双门个数的减少，也有利于增加分布制备的成功率，量子线路图如下所示。

参数:

• qubit (QVec) -- 编码比特列表。

• data (List[float] 或 List[complex]) -- 编码数据。

• layers (int) -- 表示MPS解纠缠的所需的近似层数，一般来说，层数越多，近似度越高, 默认值为3。

• sweep (int) -- 表示通过环境张量优化迭代次数，默认值为100。

• double2float (bool) -- 表示将数据向量的类型从双精度变为单精度。

返回:

None

返回类型:

None

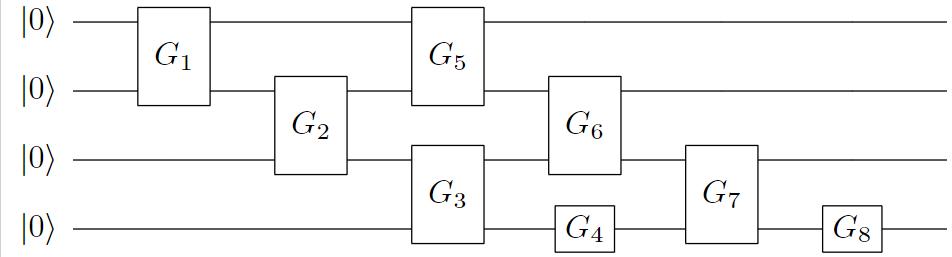
可以发现该函数支持多种类型数据制备（float，double，complex），其中layers指的是使用矩阵乘积态近似的层数，sweeps是指通过环境张量优化的迭代次数，double2float则是表示是否需要将双精度数据转为单精度类型处理，从而加速生成线路。环境张量的数学表达如下：

\[\begin{aligned} \hat{\mathcal{F}}_m=\operatorname{Tr}_{\bar{U}_m}\left[\prod_{i=M}^{m+1} U_i\left|\psi_{\chi_{\max }}\right\rangle\left\langle 0^{\otimes N}\right| \prod_{j=1}^{m-1} U_j^{\dagger}\right] \end{aligned}\]

其中， \(\operatorname{Tr}_{\bar{U}_m}\) 指的是不与 \(U_m\) 相互作用的量子比特索引上的偏迹，环境张量 \(\hat{\mathcal{F}}_m\) 则被表示为一个4x4的矩阵，在实际中可以通过从量子线路中移除 \(U_m\) 并收缩剩余的张量来计算(见下图)，并同时始终保持MPS结构。 最后，为了适配芯片的拓扑结构，该制备算法的 \(chi\) 均为2。

下面，我们以W-state作为示例，展示MPS近似编码的神奇，即在无论多少比特的W-state，均可在一层解纠缠下完成准确编码。因此，针对纠缠度较低的数据，如正太分布数据，可在一个较低深度下近似表达。

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine = CPUQVM()
    machine.init_qvm()

    n_qubits = 5
    w_state = [0]*2**n_qubits
    for i in range(n_qubits):
        w_state[1<<i] = 1/np.sqrt(n_qubits)
    w_state = np.asarray(w_state)
    qubit = machine.qAlloc_many(n_qubits)
    cir_encode = Encode()
    cir_encode.approx_mps(qubit,data = w_state,layers=1)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

          ┌─────────────┐ ┌─────────────┐ ┌────────────┐ ┌────────────┐        ┌─────────────┐        >
q_0:  |0>─┤RZ(-1.570796)├ ┤RY(-1.570796)├ ┤RZ(4.712389)├ ┤RX(1.570796)├ ───■── ┤RX(-1.570796)├ ───■── >
          ├─────────────┤ ├────────────┬┘ └────────────┘ └────────────┘ ┌──┴─┐ ├─────────────┤ ┌──┴─┐ >
q_1:  |0>─┤RY(-0.463648)├ ┤RZ(3.141593)├─ ────────────── ────────────── ┤CNOT├ ┤RY(-1.107149)├ ┤CNOT├ >
          ├─────────────┤ ├────────────┴┐                               └────┘ └─────────────┘ └────┘ >
q_2:  |0>─┤RZ(-1.178097)├ ┤RZ(-1.178097)├ ────────────── ────────────── ────── ─────────────── ────── >
          ├────────────┬┘ ├─────────────┤                                                             >
q_3:  |0>─┤RZ(5.497787)├─ ┤RY(-1.570796)├ ────────────── ────────────── ────── ─────────────── ────── >
          ├────────────┴┐ ├─────────────┤                                                             >
q_4:  |0>─┤RZ(-1.963495)├ ┤RZ(-1.963495)├ ────────────── ────────────── ────── ─────────────── ────── >
          └─────────────┘ └─────────────┘                                                             >

         ┌─────────────┐ ┌────────────┐  ┌─────────────┐ ┌────────────┐                                       >
q_0:  |0>┤RX(-1.570796)├ ┤RZ(3.141593)├─ ┤U1(-4.712389)├ ┤RZ(4.712389)├ ────────────── ────── ─────────────── >
         ├─────────────┤ ├────────────┴┐ ├────────────┬┘ ├────────────┤ ┌────────────┐        ┌─────────────┐ >
q_1:  |0>┤RY(-1.570796)├ ┤RZ(-4.712389)├ ┤RZ(2.748894)├─ ┤RZ(2.748894)├ ┤RX(1.570796)├ ───■── ┤RX(-1.047198)├ >
         └─────────────┘ └─────────────┘ └────────────┘  └────────────┘ └────────────┘ ┌──┴─┐ ├─────────────┤ >
q_2:  |0>─────────────── ─────────────── ─────────────── ────────────── ────────────── ┤CNOT├ ┤RY(-1.047198)├ >
                                                                                       └────┘ └─────────────┘ >
q_3:  |0>─────────────── ─────────────── ─────────────── ────────────── ────────────── ────── ─────────────── >
                                                                                                              >
q_4:  |0>─────────────── ─────────────── ─────────────── ────────────── ────────────── ────── ─────────────── >
                                                                                                              >

                                                                                                      >
q_0:  |0>────── ─────────────── ─────────────── ─────────────── ─────────────── ────── ────────────── >
                ┌─────────────┐ ┌─────────────┐ ┌─────────────┐                                       >
q_1:  |0>───■── ┤RX(-1.570796)├ ┤RZ(-2.748894)├ ┤RZ(-2.748894)├ ─────────────── ────── ────────────── >
         ┌──┴─┐ ├────────────┬┘ ├────────────┬┘ ├────────────┬┘ ┌─────────────┐                       >
q_2:  |0>┤CNOT├ ┤RZ(1.178097)├─ ┤RZ(1.178097)├─ ┤RZ(3.926991)├─ ┤RY(-1.570796)├ ───■── ────────────── >
         └────┘ └────────────┘  └────────────┘  └────────────┘  └─────────────┘ ┌──┴─┐ ┌────────────┐ >
q_3:  |0>────── ─────────────── ─────────────── ─────────────── ─────────────── ┤CNOT├ ┤RZ(0.615480)├ >
                                                                                └────┘ └────────────┘ >
q_4:  |0>────── ─────────────── ─────────────── ─────────────── ─────────────── ────── ────────────── >
                                                                                                      >

                                                                                                     >
q_0:  |0>────────────── ────── ────────────── ────── ─────────────── ─────────────── ─────────────── >
                                                                                                     >
q_1:  |0>────────────── ────── ────────────── ────── ─────────────── ─────────────── ─────────────── >
                        ┌────┐ ┌────────────┐        ┌─────────────┐ ┌─────────────┐ ┌─────────────┐ >
q_2:  |0>────────────── ┤CNOT├ ┤RX(0.000000)├ ───■── ┤RX(-1.570796)├ ┤RZ(-3.141593)├ ┤RY(-1.570796)├ >
         ┌────────────┐ └──┬─┘ ├────────────┤ ┌──┴─┐ ├────────────┬┘ ├─────────────┤ ├─────────────┤ >
q_3:  |0>┤RX(1.570796)├ ───■── ┤RY(0.615480)├ ┤CNOT├ ┤RZ(3.141593)├─ ┤RY(-1.570796)├ ┤RZ(-0.785398)├ >
         └────────────┘        └────────────┘ └────┘ └────────────┘  └─────────────┘ └─────────────┘ >
q_4:  |0>────────────── ────── ────────────── ────── ─────────────── ─────────────── ─────────────── >
                                                                                                     >


q_0:  |0>─────────────── ─────────────── ────────────── ────── ─────────────── ────── ─────────────── ─────────────── ──────────────

q_1:  |0>─────────────── ─────────────── ────────────── ────── ─────────────── ────── ─────────────── ─────────────── ──────────────
         ┌─────────────┐ ┌─────────────┐ ┌────────────┐
q_2:  |0>┤RZ(-2.356194)├ ┤U1(-6.283185)├ ┤RZ(6.283185)├ ────── ─────────────── ────── ─────────────── ─────────────── ──────────────
         ├─────────────┤ ├─────────────┤ ├────────────┤        ┌─────────────┐        ┌─────────────┐ ┌────────────┐  ┌────────────┐
q_3:  |0>┤RZ(-2.748894)├ ┤RZ(-2.748894)├ ┤RX(1.570796)├ ───■── ┤RX(-0.785398)├ ───■── ┤RX(-1.570796)├ ┤RZ(1.178097)├─ ┤RZ(1.178097)├
         └─────────────┘ └─────────────┘ └────────────┘ ┌──┴─┐ ├─────────────┤ ┌──┴─┐ ├─────────────┤ ├────────────┴┐ └────────────┘
q_4:  |0>─────────────── ─────────────── ────────────── ┤CNOT├ ┤RY(-0.785398)├ ┤CNOT├ ┤RZ(-2.748894)├ ┤RZ(-2.748894)├ ──────────────
                                                        └────┘ └─────────────┘ └────┘ └─────────────┘ └─────────────┘


{'00000': 4.468157470978386e-32, '00001': 0.20000000000000048, '00010': 0.2000000000000004, '00011': 0.0, '00100': 0.20000000000000048, '00101': 7.4987989133093034e-34, '00110': 7.498798913309305e-34, '00111': 0.0, '01000': 0.20000000000000023, '01001': 1.4102295515520025e-35, '01010': 1.4102295515519843e-35, '01011': 0.0, '01100': 4.818833738106373e-33, '01101': 9.629649721936199e-35, '01110': 1.1555579666323412e-33, '01111': 0.0, '10000': 0.20000000000000023, '10001': 1.410229551551963e-35, '10010': 1.4102295515519827e-35, '10011': 0.0, '10100': 4.818833738106368e-33, '10101': 9.629649721936196e-35, '10110': 1.1555579666323415e-33, '10111': 0.0, '11000': 0.0, '11001': 3.851859888774471e-34, '11010': 0.0, '11011': 0.0, '11100': 3.851859888774471e-34, '11101': 5.934729841099873e-67, '11110': 0.0, '11111': 0.0}

ds_quantum_state_preparation(qubit, data)

双稀疏量子态编码[5]通过利用 \(n\) 个辅助比特辅助构建线路。我们以编码 \(|001\rangle\) 为例，如下图所示：

参数:

• qubit (QVec) -- 编码比特列表。

• data (List[float] 或 List[complex]) -- 编码数据。

返回:

None

返回类型:

None

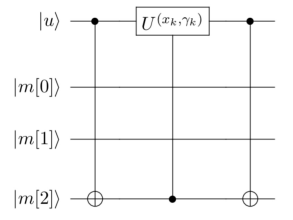
其中，\(|\mu\rangle\) 为辅助寄存器用以作用旋转门，并受输出寄存器 \(|m\rangle\) 控制，而当所需编码的字符下标的1的个数较多时，则需要作用多控门，而为了减少消除线路中多控门的数量，我们 通过增加一部分辅助寄存器，并利用Toffoli门进行分解，其原理如下图所示：

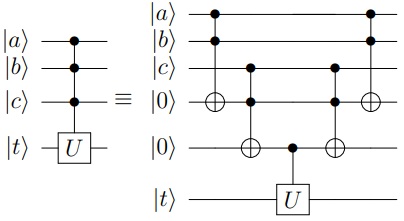from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine = CPUQVM()
    machine.init_qvm()
    data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
    data = np.asarray(data)
    qubit = machine.qAlloc_many(6)
    cir_encode = Encode()
    cir_encode.ds_quantum_state_preparation(qubit,data)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

          ┌─┐        ┌───────────────────────────────┐                          ┌───────────────────────────────┐ >
q_0:  |0>─┤X├ ───■── ┤U3(-1.230959,0.000000,0.000000)├ ───■── ───■── ───■── ─── ┤U3(-1.570796,0.000000,0.000000)├ >
          └─┘    │   └───────────────┬───────────────┘    │      │      │   ┌─┐ └───────────────┬───────────────┘ >
q_2:  |0>──── ───┼── ────────────────┼──────────────── ───┼── ───┼── ───┼── ┤X├ ────────────────■──────────────── >
              ┌──┴─┐                 │                 ┌──┴─┐ ┌──┴─┐    │   └┬┘                                   >
q_3:  |0>──── ┤CNOT├ ────────────────■──────────────── ┤CNOT├ ┤CNOT├ ───┼── ─■─ ───────────────────────────────── >
              └────┘                                   └────┘ └────┘    │    │                                    >
q_4:  |0>──── ────── ───────────────────────────────── ────── ────── ───┼── ─┼─ ───────────────────────────────── >
                                                                     ┌──┴─┐  │                                    >
q_5:  |0>──── ────── ───────────────────────────────── ────── ────── ┤CNOT├ ─■─ ───────────────────────────────── >
                                                                     └────┘                                       >

                                             ┌───────────────────────────────┐
q_0:  |0>─── ───■── ───■── ───■── ───■── ─── ┤U3(-3.141593,0.000000,0.000000)├ ───
         ┌─┐    │      │      │      │   ┌─┐ └───────────────┬───────────────┘ ┌─┐
q_2:  |0>┤X├ ───┼── ───┼── ───┼── ───┼── ┤X├ ────────────────■──────────────── ┤X├
         └┬┘ ┌──┴─┐    │      │      │   └┬┘                                   └┬┘
q_3:  |0>─■─ ┤CNOT├ ───┼── ───┼── ───┼── ─┼─ ───────────────────────────────── ─┼─
        │    └────┘    │   ┌──┴─┐    │    │                                     │
q_4:  |0>─┼─ ────── ───┼── ┤CNOT├ ───┼── ─■─ ───────────────────────────────── ─■─
        │           ┌──┴─┐ └────┘ ┌──┴─┐  │                                     │
q_5:  |0>─■─ ────── ┤CNOT├ ────── ┤CNOT├ ─■─ ───────────────────────────────── ─■─
                    └────┘        └────┘


{'000': 0.0, '001': 0.3333333333333333, '010': 0.0, '011': 0.0, '100': 0.0, '101': 0.3333333333333334, '110': 0.33333333333333315, '111': 0.0}

sparse_isometry(qubit, data)

sparse_isometry编码[6]不同于双稀疏量子态编码需要辅助比特去构建线路。 sparse_isometry编码首先通过将长度为 \(N\) 稀疏数据向量中的非0元素 \(x\) 统一编码至前 \(\lceil log_2len(x) \rceil\) 个量子比特上，后通过受控X门对其进行受控转化。其线路构建如下图所示：

参数:

• qubit (QVec) -- 编码比特列表。

• data (List[float] 或 List[complex]) -- 编码数据。

返回:

None

返回类型:

None

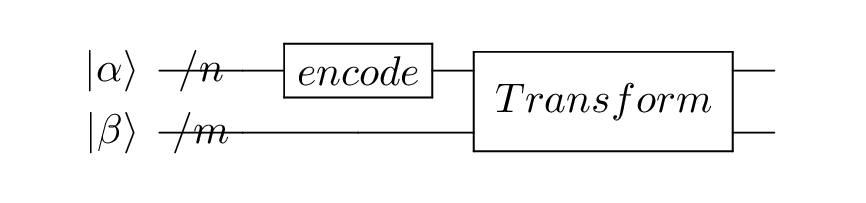
其中，\(n+m=\lceil log_2N \rceil\) \(|\alpha\rangle\) 为 \(\lceil log_2len(x) \rceil\) 个非0元素的编码encode模块， 而 \(|\beta\rangle\) 则为剩余qubit。 其中transform模块则是转化模块。

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine = CPUQVM()
    machine.init_qvm()
    data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
    data = np.asarray(data)
    qubit = machine.qAlloc_many(3)
    cir_encode = Encode()
    cir_encode.sparse_isometry(qubit,data)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

                         ┌────────────┐     ┌────────────┐ ┌─┐     ┌─┐ ┌─┐ ┌─┐     ┌─┐ ┌─┐
q_0:  |0>─────────────── ┤RY(0.000000)├ ─── ┤RY(1.570796)├ ┤X├ ─■─ ┤X├ ┤X├ ┤X├ ─■─ ┤X├ ┤X├
          ┌────────────┐ └──────┬─────┘ ┌─┐ └──────┬─────┘ ├─┤  │  ├─┤ └┬┘ └─┘  │  ├─┤ └┬┘
q_1:  |0>─┤RY(1.230959)├ ───────■────── ┤X├ ───────■────── ┤X├ ─■─ ┤X├ ─┼─ ─── ─■─ ┤X├ ─┼─
          └────────────┘                └─┘                └─┘ ┌┴┐ └─┘  │      ┌┴┐ └─┘  │
q_2:  |0>─────────────── ────────────── ─── ────────────── ─── ┤X├ ─── ─■─ ─── ┤X├ ─── ─■─
                                                               └─┘             └─┘


{'000': 0.0, '001': 0.3333333333333334, '010': 0.0, '011': 0.0, '100': 0.0, '101': 0.3333333333333333, '110': 0.3333333333333333, '111': 0.0}

efficient_sparse(qubit, data)

多项式稀疏量子态编码[7]是一种稀疏数据向量中的非0元素个数与qubit个数成线性关系的稀疏数据编码方式。其线路编码深度为 \(O\left(|S|^{2} \log (|S|) n\right)\) 。 其中，\(|S|\) 为非0元素个数，\(n\) 为所需qubit个数，即为 \(\lceil log_2N \rceil\) , \(N\) 为稀疏数据长度。下面以编码 \(|x\rangle=1/\sqrt{3}(|001\rangle+|100\rangle+|111\rangle)\) 为例，其线路图构建如下：

参数:

• qubit (QVec) -- 编码比特列表。

• data (List[float] 或 List[complex]) -- 编码数据。

返回:

None

返回类型:

None

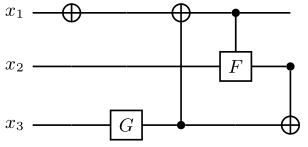
其中，F门是将 \(|0\rangle\) 映射到 \(1/\sqrt{3}|0\rangle+1/\sqrt{3}|1\rangle\) ，而G门则是将 \(|0\rangle\) 映射到 \(1/\sqrt{3}|0\rangle+2/\sqrt{3}|1\rangle\)。

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine = CPUQVM()
    machine.init_qvm()
    data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
    data = np.asarray(data)
    qubit = machine.qAlloc_many(3)
    cir_encode = Encode()
    cir_encode.efficient_sparse(qubit,data)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

          ┌─┐                                      ┌────┐                                             >
q_0:  |0>─┤X├ ──────────────────────────────────── ┤CNOT├ ────── ──────────────────────────────────── >
          └─┘                                      └──┬─┘ ┌────┐                                      >
q_1:  |0>──── ──────────────────────────────────── ───┼── ┤CNOT├ ──────────────────■───────────────── >
          ┌─┐ ┌──────────────────────────────────┐    │   └──┬─┘ ┌─────────────────┴────────────────┐ >
q_2:  |0>─┤X├ ┤U3(1.230959,0.000000,0.000000).dag├ ───■── ───■── ┤U3(1.570796,0.000000,0.000000).dag├ >
          └─┘ └──────────────────────────────────┘               └──────────────────────────────────┘ >

         ┌────┐
q_0:  |0>┤CNOT├ ────── ───
         └──┬─┘ ┌────┐
q_1:  |0>───┼── ┤CNOT├ ───
            │   └──┬─┘ ┌─┐
q_2:  |0>───■── ───■── ┤X├
                       └─┘


{'000': 0.0, '001': 0.3333333333333333, '010': 0.0, '011': 0.0, '100': 0.0, '101': 0.3333333333333333, '110': 0.3333333333333334, '111': 0.0}

iqp_encode(qubit, data, control_vector=None, inverse=false, repeats=1)

IQP编码[8] iqp_encode(qubit, data, control_vector = None, inverse=false, repeats = 1) 是一种应用于量子机器学习的编码方法。将一个经典数据x编码到

\[\begin{aligned} |\mathbf{x}\rangle=\left(\mathrm{U}_{\mathrm{Z}}(\mathbf{x}) \mathrm{H}^{\otimes n}\right)^{\boldsymbol{r}}\left|0^{n}\right\rangle \end{aligned}\]

其中， \(r\) 表示量子线路的深度，也就是 \(\mathrm{U}_{\mathrm{Z}}(\mathbf{x}) \mathrm{H}^{\otimes n}\) 重复的次数。\(\mathrm{H}^{\otimes n}\) 是一层作用在所有量子比特上的Hadamard门。其中， \(\mathrm{U}_\mathrm{Z}\) 为

\[\begin{aligned} \mathrm{U}_\mathrm{Z}(\mathbf{x})=\prod_{[i, j] \in S} R_{Z_{i} Z_{j}}\left(x_{i} x_{j}\right) \bigotimes_{k=1}^{n} R_{z}\left(x_{k}\right) \end{aligned}\]

这里的 \(S\) 是一个集合，对于这个集合中的每一对量子比特，我们都需要对它们作用 \(R_{ZZ}\) 门。\(R_{ZZ}\) 门的构建形式如下：

参数:

• qubit (QVec) -- 编码比特列表。

• data (List[float]) -- 编码数据。

• control_vector (List[tuple]) -- 控制序列，默认为空，则表示按序控制。

• inverse (int) -- 是否翻转线路，默认为False。

• inverse -- 表示重复模块次数，默认为1。

返回:

None

返回类型:

None

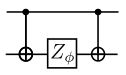
下面我们以编码 \(data=[-1.3, 1.8, 2.6, -0.15]\) 为例介绍：

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine=CPUQVM()
    machine.init_qvm()

    data = [-1.3, 1.8, 2.6, -0.15]
    data = np.asarray(data)
    qubit = machine.qAlloc_many(4)
    cir_encode = Encode()
    cir_encode.iqp_encode(qubit,data)
    prog = QProg()
    prog << cir_encode.get_circuit()
    print(prog)
    encode_qubits = cir_encode.get_out_qubits()
    machine.directly_run(prog)
    result = machine.get_qstate()
    print(result)
    machine.finalize()

          ┌─┐ ┌─────────────┐
q_0:  |0>─┤H├ ┤RZ(-1.300000)├ ───■── ─────────────── ───■── ────── ────────────── ────── ────── ─────────────── ──────
          ├─┤ ├────────────┬┘ ┌──┴─┐ ┌─────────────┐ ┌──┴─┐
q_1:  |0>─┤H├ ┤RZ(1.800000)├─ ┤CNOT├ ┤RZ(-2.340000)├ ┤CNOT├ ───■── ────────────── ───■── ────── ─────────────── ──────
          ├─┤ ├────────────┤  └────┘ └─────────────┘ └────┘ ┌──┴─┐ ┌────────────┐ ┌──┴─┐
q_2:  |0>─┤H├ ┤RZ(2.600000)├─ ────── ─────────────── ────── ┤CNOT├ ┤RZ(4.680000)├ ┤CNOT├ ───■── ─────────────── ───■──
          ├─┤ ├────────────┴┐                               └────┘ └────────────┘ └────┘ ┌──┴─┐ ┌─────────────┐ ┌──┴─┐
q_3:  |0>─┤H├ ┤RZ(-0.150000)├ ────── ─────────────── ────── ────── ────────────── ────── ┤CNOT├ ┤RZ(-0.390000)├ ┤CNOT├
          └─┘ └─────────────┘                                                            └────┘ └─────────────┘ └────┘


[(-0.1925578135118269-0.15944117553362588j), (0.24534942018697528+0.047996479182488616j), (-0.02973039232415307+0.24822591277352968j), (-0.22912120333719244+0.10001736939810474j), (-0.06725827577934981-0.2407827326433292j), (0.17417667733679137+0.17933902272488078j), (0.1777283845030693-0.17581985480010265j), (0.2415974945336283+0.06427013797303885j), (-0.24713295520684903-0.037753178021585905j), (0.23511504508229614-0.08497597057962829j), (0.10212186022103938+0.22819098506513033j), (-0.14509671578880565+0.20358522310644894j), (-0.008095829439931083-0.249868880706821j), (0.1265550643081946+0.2156010568108347j), (0.21442717034095604-0.12853399791327838j), (0.21939564047259316+0.11985638465105079j)]

[1] Schuld, Maria. "Quantum machine learning models are kernel methods."[J] arXiv:2101.11020 (2021).
[2] Araujo I F, Park D K, Ludermir T B, et al. "Configurable sublinear circuits for quantum state preparation."[J]. arXiv preprint arXiv:2108.10182, 2021.
[3] Ghosh K. "Encoding classical data into a quantum computer"[J]. arXiv preprint arXiv:2107.09155, 2021.
[4] Rudolph M S, Chen J, Miller J, et al. Decomposition of matrix product states into shallow quantum circuits[J]. arXiv preprint arXiv:2209.00595, 2022.
[5] de Veras T M L, da Silva L D, da Silva A J. "Double sparse quantum state preparation"[J]. arXiv preprint arXiv:2108.13527, 2021.
[6] Malvetti E, Iten R, Colbeck R. "Quantum circuits for sparse isometries"[J]. Quantum, 2021, 5: 412.
[7] N. Gleinig and T. Hoefler, "An Efficient Algorithm for Sparse Quantum State Preparation," 2021 58th ACM/IEEE Design Automation Conference (DAC), 2021, pp. 433-438, doi: 10.1109/DAC18074.2021.9586240.
[8] Havlíček, Vojtěch, et al. "Supervised learning with quantum-enhanced feature spaces." Nature 567.7747 (2019): 209-212.