基础逻辑门转换

简介

在NISQ时代，量子计算机无法做到任意逻辑门的运行。因此需要将其转化为量子芯片所支持的基础逻辑门集合以实现通用计算。在本源量子芯片中所支持的单双门组合则为 \(U_3\) 和 \(CZ\) 。 因此，在编译量子程序时，QPanda会对非基础逻辑门进行转换。

原理

首先，定义 \(\phi\) 为 \(XY\) 平面内某一旋转轴与 \(X\) 正向的夹角，则对任意 \(XY\) 旋转门，有：

\[\begin{split}\begin{aligned} R_\phi(\theta) = cos\frac{\theta}{2}I - i sin\frac{\theta}{2}(cos\phi\sigma_x + sin\phi\sigma_y) = \begin{pmatrix} cos\frac{\theta}{2} & -i sin\frac{\theta}{2}e^{-i\phi} \\ -isin\frac{\theta}{2}e^{i\phi} & cos\frac{\theta}{2} \end{pmatrix} \end{aligned}\end{split}\]

Z旋转门的形式如下：

\[\begin{split}\begin{aligned} R_Z(\theta) = cos\frac{\theta}{2}I - i sin\frac{\theta}{2}\sigma_Z = \begin{pmatrix} 1 & 0 \\ 0 & e^{i\theta} \end{pmatrix} \end{aligned}\end{split}\]

易证：

\[\begin{aligned} R_X(\theta_X)R_Z(\theta_Z) = R_Z(\theta_Z)R_{-\theta_Z}(\theta_X) \end{aligned}\]
\[\begin{aligned} R_Z(\theta_{Z2})R_Z(\theta_{Z1}) = R_Z(\theta_{Z1} + \theta_{Z2}) \end{aligned}\]
\[\begin{aligned} CZ[R_Z(\theta_{Z1}) \otimes R_Z(\theta_{Z2})] = [ R_Z(\theta_{Z1} \otimes R_Z(\theta_{Z2}) ]·CZ \end{aligned}\]

以上公式是Virtual Z 门的基础。它意味着，我们可以将线路中已有的Z操作转移到XY操作之后，作为替代，原XY操作的旋转轴将随之变换。而被转移到线路后排的Z操作可以合并，并继续转移，以此类推。

这里我们用单比特的SU(2)门来举例证明：

\[\begin{split}\begin{aligned} U(\theta , \phi ,\lambda) = \begin{bmatrix} cos\frac{\theta}{2} & -isin\frac{\theta}{2}e^{i\lambda} \\ -isin\frac{\theta}{2}e^{i\phi} & cos\frac{\theta}{2}e^{i(\lambda + \phi)} \end{bmatrix} \end{aligned}\end{split}\]

利用

\[\begin{aligned} R_X(\theta) = R_Z(-\frac{\pi}{2})R_X(\frac{\pi}{2})R_Z(\pi - \theta)R_X(\frac{\pi}{2})R_Z(-\frac{\pi}{2}) \end{aligned}\]

最终得到

\[\begin{aligned} U(\theta , \phi ,\lambda) = R_Z(\phi - \frac{\pi}{2})R_X(\frac{\pi}{2})R_Z(\pi - \theta)R_X(\frac{\pi}{2})R_Z(\lambda - \frac{\pi}{2}) = R_Z(\phi + \lambda - \theta)R_{\frac{\pi}{2} + \lambda - \theta}(\frac{\pi}{2})R_{\lambda - \frac{\pi}{2}}(\frac{\pi}{2}) \end{aligned}\]

可见，任意的SU(2)门都可以轻易转化成两个任意旋转轴的 \(\pi/2\) 门，以及一个Vritual Z 门。

代码示例

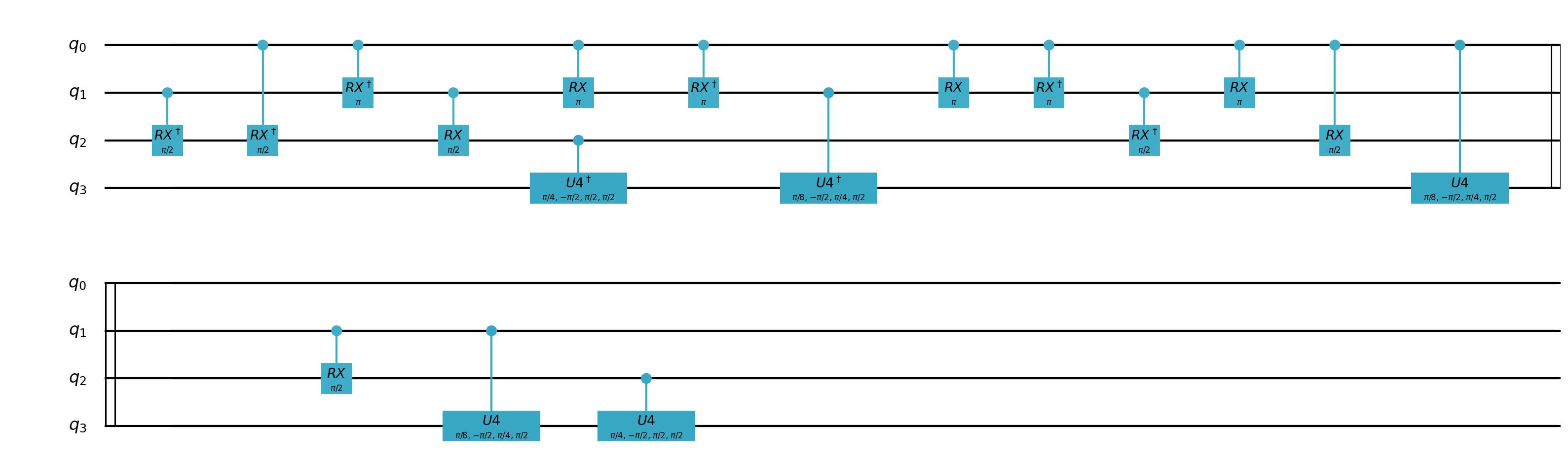
这里我们对前一节QSD分解之后的线路使用Vritual Z 门进行转换,只需要执行下面这行代码即可。

from pyqpanda import *
import numpy as np
from scipy.stats import unitary_group

if __name__ == "__main__":
    machine = CPUQVM()
    machine.init_qvm()
    q = machine.qAlloc_many(3)
    c = machine.cAlloc_many(3)

    # 生成任意酉矩阵
    unitary_matrix = unitary_group.rvs(2**3,random_state=169384)

    # 输入需要被分解的线路
    prog = QProg()
    prog<<matrix_decompose(q,unitary_matrix,mode=DecompositionMode.QSDecomposition)
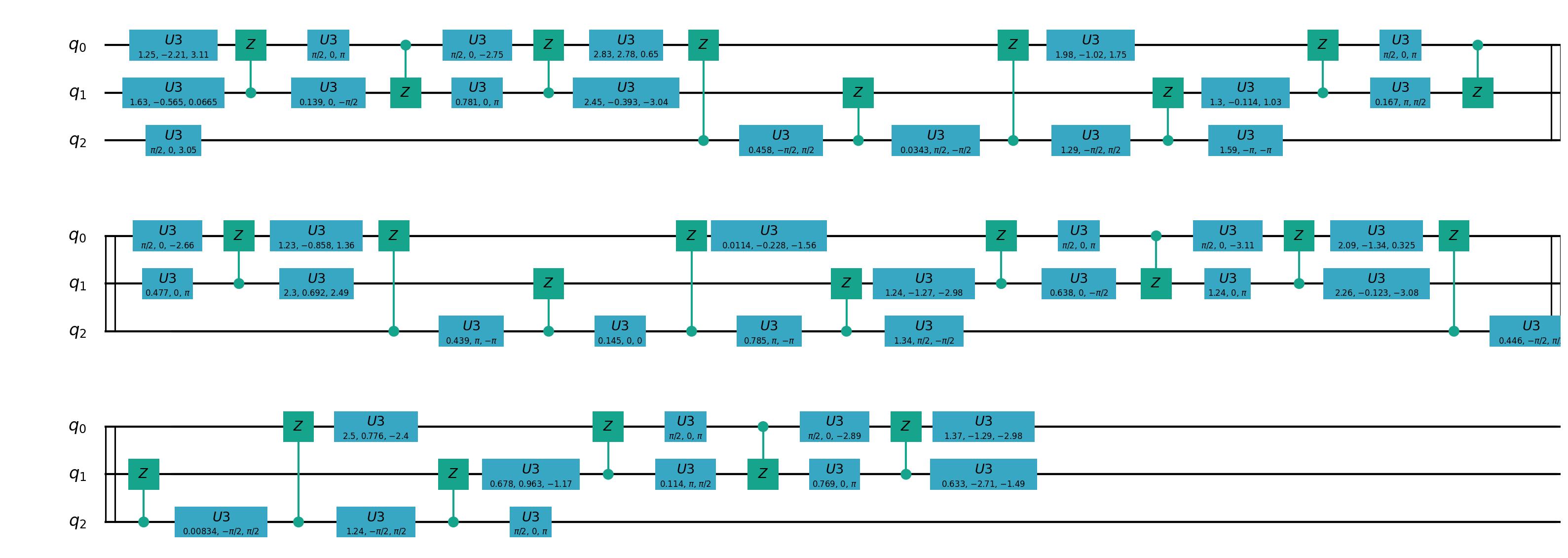
    virtual_prog = virtual_z_transform(prog, machine)
    draw_qprog(prog, "pic")
../_images/QCircuit_virtualz.jpg

基础逻辑门转换

在量子计算的量子线路设计中，基础逻辑门的标准表示形式是量子门集合的一种形式。这些基础门包括Hadamard门（H门）、Pauli门（X门、Y门、Z门）、CNOT门等。然而，在实际的量子线路设计和优化过程中，经常需要进行基础逻辑门的转换，以便更好地适应特定的硬件或算法需求。

一个常见的转换任务是将带有角度参数的单比特门（例如相位门）转换为通用的单比特门形式，如U3门。U3门是一个通用的单比特量子门，可以表示任意的单比特旋转操作。这样的转换可以提高线路的灵活性，使得线路更容易优化和映射到不同的量子硬件上。

作为基础逻辑门转换的接口，我们提供了一组功能强大的工具，用于将不同形式的基础门相互转换。用户可以使用这些接口来实现自定义的门转换策略，以满足其特定的设计需求。这些接口支持将门转换为等效的门序列，同时保留线路的功能等效性。这样的门转换工具对于量子编译器和量子线路优化的各个阶段都具有重要的作用。

我们使用 transform_to_base_qgate 进行基础门转换，接口定义如下

transform_to_base_qgate

transform_to_base_qgate(qprog: QProg, machine: QuantumMachine, convert_single_gates: List[str], convert_double_gates: List[str]) → QProg

Basic quantum gate conversion

Args:

qprog (QProg): Quantum program machine (QuantumMachine): Quantum machine convert_single_gates (List[str]): List of quantum single gates to convert convert_double_gates (List[str]): List of quantum double gates to convert

Returns:

QProg: A new quantum program after the transformation

This function performs basic quantum gate conversion on the given quantum program using the specified quantum machine. It allows the conversion of specific sets of single and double gates, as defined by the lists convert_single_gates and convert_double_gates, respectively.

from pyqpanda import *
from typing import List

qprog = QProg()
machine = QuantumMachine()
convert_single_gates = ["H", "T"]
convert_double_gates = ["CNOT", "CZ"]

# Perform quantum gate conversion
new_qprog = transform_to_base_qgate(qprog, machine, convert_single_gates, convert_double_gates)

# Print the new quantum program
print(new_qprog)

量子比特映射

简介

量子比特映射是指在量子计算中，将抽象的量子逻辑比特（qubit）映射到物理系统中的实际量子比特上的过程。由于量子计算机的构建涉及物理层面的限制和噪声，因此需要将抽象的量子逻辑转化为在实际量子硬件上可以操作的形式。 在量子计算中，一个量子逻辑比特是抽象的计算单元，通常被建模为一个复数的线性组合。然而，实际的量子硬件（比如量子比特在量子芯片上的物理实现）可能受到噪声、耦合等因素的影响，因此需要将量子逻辑比特映射到物理比特上。这个映射通常是一个复杂的过程，涉及硬件架构、噪声特性、量子门的实现等。 其中最为受限的则是纠缠映射，如果计算中需要纠缠操作，那么需要将逻辑上的纠缠映射到物理上的纠缠，同时考虑硬件的限制。

算法原理

Sabre算法

Sabre算法是一种适用于任意比特之间连接的量子拓扑结构，引入衰减效应来优化搜索步骤减少生成线路的深度，最后将逻辑比特映射到物理比特上。接下来介绍该算法在量子线路上的实际应用。 下图展示本源量子计算机中一种量子拓扑结构，我们用双向箭头来表示两个直接相邻的量子比特。

../_images/BY.PNG

由于在物理层面上存在量子比特排布的限制，只能允许两个相邻的量子比特之间进行计算。例如在这个图中，\(Q_0\) 和 \(Q_1\) ， \(Q_7\) 通过耦合器直接相连，我们可以在 \(\{ Q_0,Q_5\}\) , \(\{ Q_0,Q_7\}\) 这两组量子比特之间插入CNOT门。 但是如果我们想要在 \(\{ Q_0,Q_6\}\) 之间插入CNOT门的话，是无法直接实现的，因为 \(Q_0\) 和 \(Q_6\) 不直接相连。也就是说，我们无法直接在两个不相连的量子比特之间插入一个CNOT门。

接下来，我们使用下图中一个简单4比特的量子线路来说明量子比特映射中的问题。在这个结构中，被允许直接进行计算的量子对有：\(\{ Q_0,Q_1\}\), \(\{ Q_1,Q_2\}\), \(\{ Q_2,Q_3\}\), \(\{ Q_3,Q_0\}\) ，不能直接进行计算的有：\(\{ Q_0,Q_2\}\) , \(\{ Q_1,Q_3\}\) 。对于给出的含有三个CNOT门的量子线路中，我们假定初始逻辑比特和物理比特的映射关系是 \(\{ q_0 \mapsto Q_0, q_1 \mapsto Q_1, q_2 \mapsto Q_2, q_3 \mapsto Q_3,\}\) 。

../_images/4topo.PNG

在图中，我们发现门 \(G_2\) 连接的两个量子比特是 \(Q_0\) 和 \(Q_2\) ，但是这样的CNOT门在实际的计算机中无法实现，因此我们通过使用SWAP门， 来移动 \(Q_0\) 或者 \(Q_2\) 的位置，使它们相邻并可以计算。通过在下图中，插入两个SWAP门，就可以使线路中所有的SWAP门可以进行计算。

../_images/swap_exa.PNG

Sabre算法就是通过寻找可以插入SWAP门的位置，来对线路进行优化，使得原本不可以在量子计算机上运行的量子门，通过动态的改变量子比特的邻接位来使得所有的量子门都能够进行计算。 以前的工作通常采用基于映射的穷举式搜索来寻找有效的映射转换。Sabre通过设计一个启发式成本函数，通过限制生成线路的深度，来帮助找到插入SWAP门的位置。

pyqpanda中基于sabre映射算法的接口是 sabre_mapping 。

sabre_mapping(prog: QProg, quantum_machine: QuantumMachine, init_map: List[int], max_look_ahead: int = 20, max_iterations: int = 10, config_data: str = 'QPandaConfig.json') → QProg

该函数执行 Sabre 映射算法，用于对给定量子程序进行映射以优化其执行,支持多种重载形式。

参数:

  • prog (QProg) -- 目标量子程序。

  • quantum_machine (QuantumMachine) -- 量子计算机。

  • init_map (List[int]) -- 初始映射列表。

  • max_look_ahead (int, optional) -- Sabre 映射的最大前瞻步数。默认为 20。

  • max_iterations (int, optional) -- Sabre 映射的最大迭代次数。默认为 10。

  • config_data (str, optional) -- 配置数据，用于加载配置。默认为 'QPandaConfig.json'。

  • arch_matrix (numpy.ndarray[numpy.float64[m,n]], optional) -- 拓扑结构矩阵，用于特定重载。

返回:

映射优化后的量子程序。

返回类型:

QProg

示例用法:

# 使用初始映射和默认参数进行 Sabre 映射
mapped_prog = sabre_mapping(my_prog, my_quantum_machine, init_map=[0, 1, 2])

# 使用自定义拓扑结构矩阵进行 Sabre 映射
custom_arch_matrix = numpy.array(...)  # 自定义拓扑结构矩阵
mapped_prog = sabre_mapping(my_prog, my_quantum_machine, init_map=[0, 1, 2], arch_matrix=custom_arch_matrix)

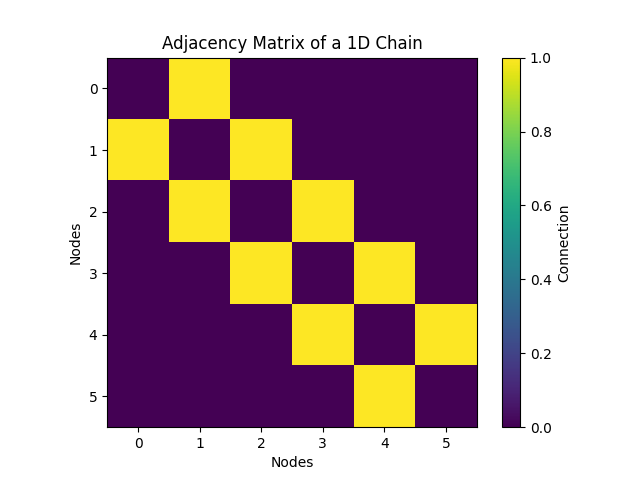
我们以一维链的邻接矩阵为例，首先构建一维链的邻接矩阵并输出

import numpy as np
import matplotlib.pyplot as plt

# 创建一个6个节点的邻接矩阵
num_nodes = 6
chain_graph = np.zeros((num_nodes, num_nodes), dtype=np.double)

for i in range(num_nodes - 1):
    chain_graph[i, i + 1] = 1
    chain_graph[i + 1, i] = 1

# 绘制邻接矩阵
plt.imshow(chain_graph, cmap='viridis', interpolation='nearest')
plt.title("Adjacency Matrix of a 1D Chain")
plt.xlabel("Nodes")
plt.ylabel("Nodes")
plt.colorbar(label="Connection")
plt.show()

可以看到一维链的结构如下图

../_images/arch.png

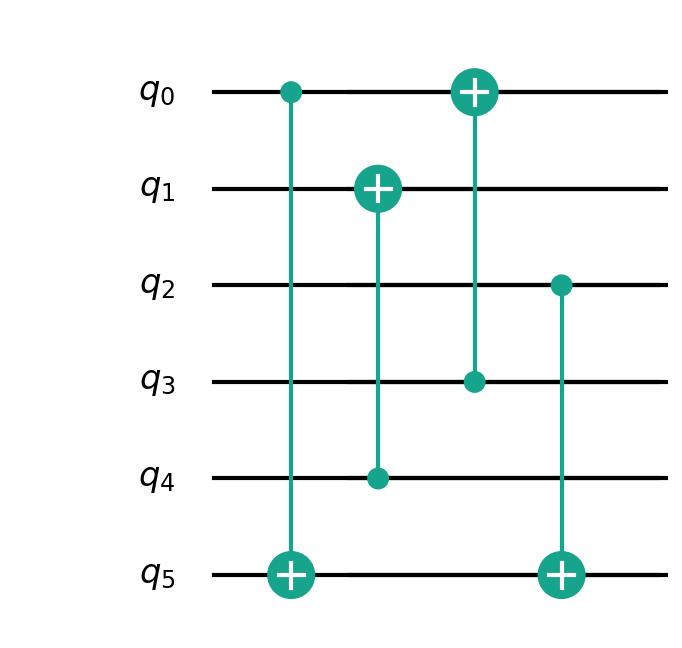
我们需要对如下量子程序进行映射

../_images/mapping.jpg

示例代码为

from pyqpanda import *
import numpy as np

if __name__ == "__main__":

    machine = CPUQVM()
    machine.init_qvm()

    q = machine.qAlloc_many(6)

    prog = QProg()
    prog << CNOT(q[0],q[5])<< CNOT(q[4],q[1])<< CNOT(q[3],q[0])<< CNOT(q[2],q[5])

    num_nodes = 6
    chain_graph = np.zeros((num_nodes, num_nodes), dtype=np.double)

    for i in range(num_nodes - 1):
        chain_graph[i, i + 1] = 1
        chain_graph[i + 1, i] = 1

    sabre_result = sabre_mapping(prog, machine, 20, 10, chain_graph)
    draw_qprog(sabre_result,'pic')

由于sabre算法具备随机性，因此映射结果并不固定，此次结果为：

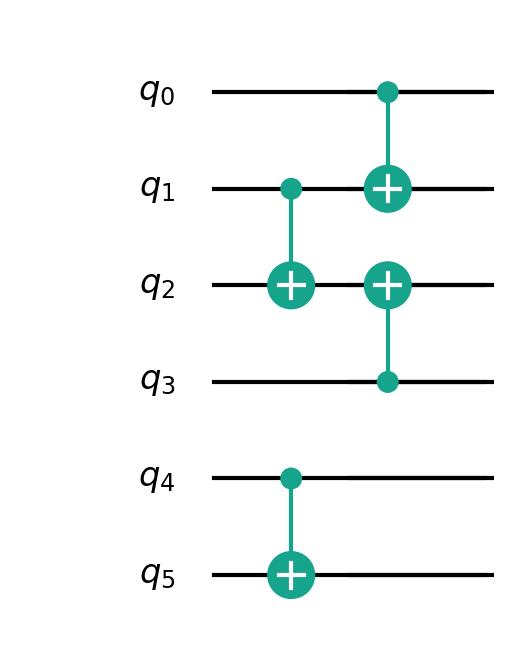
../_images/sabre_mapping.jpg

BMT算法

除了Sabre算法，BMT拓扑映射算法通过将量子程序转换称DAG(有向无环图)数据结构，通过对线路重构来生成新的量子程序。因为每次插入一个SWAP门，都相当于插入了3个CNOT门，SWAP门过多会影响线路的保真度，因此这种做法能够减少SWAP门的使用。

用一个简单的线路举例，对于一个含有3个CNOT门的线路中， \(CNOT_{0,1}\) , \(CNOT_{1,2}\) , \(CNOT_{0,2}\) ，我们可以构建如下图所示的DAG：

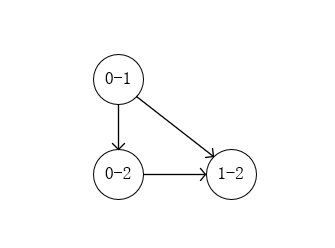
../_images/DAG.png

然后遍历DAG获取最大子图序列，循环处理执行入度为0的节点（入度为0即为该节点中逻辑门所需的比特处于空闲情况，可以执行当前节点中逻辑门），执行的节点用于构建最大子图，执行完则需要将该节点从DAG去除。处理下一个入度为0的节点。直至DAG中无节点为止。

遍历由量子程序构建的DAG，最终获得以下格式数据，多个最大子图数据和每个对应的同构子图数据和映射关系：

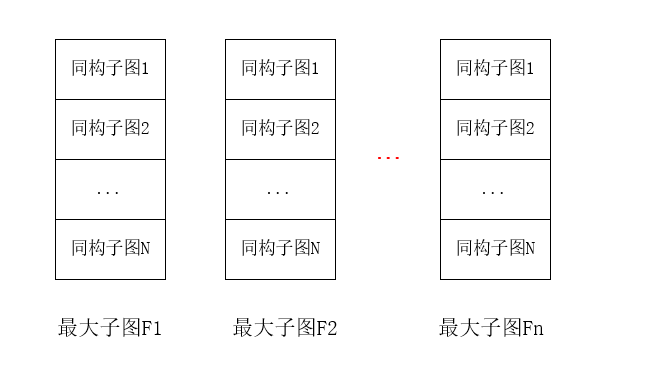
../_images/isomorphic.png

结合Token-Swapping技术，寻找最短消耗的映射方法。固定路径：这里主要考虑拓扑结构的最短距离，这里通过BFS算法确定拓扑结构两点间的固定成本。 最大子图都有着自己的映射方法，相邻的最大子图就需要各自映射方法并结合SWAP达到效果。我们就是要将每个最大子图间的SWAP最小化，同时由于每个最大子图有着多种同构情况，所以这里便是一个排列组合问题。我们要做的就是将消耗成本最低的组合情况选择出来。最后生成新的量子程序。

pyqpanda中基于bmt映射算法的接口是 OBMT_mapping 。

OBMT_mapping(prog: QProg, quantum_machine: QuantumMachine, b_optimization: bool = False, max_partial: int = 4294967295, max_children: int = 4294967295, config_data: str = 'QPandaConfig.json') → QProg

该函数用于进行BMT映射，将目标量子程序映射到指定的拓扑结构上，以获得一个映射后的量子程序。可以选择是否开启优化，并可以配置一些映射相关的参数。返回映射后的量子程序。

参数:

  • prog (QProg) -- 目标量子程序。

  • quantum_machine (QuantumMachine) -- 量子计算机。

  • b_optimization (bool, optional) -- 是否开启优化。默认为 False。

  • max_partial (int, optional) -- 每一步的最大部分解数量限制，默认为 4294967295（无限制）。

  • max_children (int, optional) -- 每个双量子门的最大候选解数量限制，默认为 4294967295（无限制）。

  • config_data (str, optional) -- 配置数据文件路径

返回:

映射后的量子程序。

返回类型:

QProg

OBMT_mapping(prog: QProg, quantum_machine: QuantumMachine, b_optimization: bool, arch_matrix: numpy.ndarray[numpy.float64[m, n]]) → QProg

该函数用于进行BMT映射，将目标量子程序映射到指定的拓扑结构上，以获得一个映射后的量子程序。可以选择是否开启优化，并可以配置一些映射相关的参数。返回映射后的量子程序。

参数:

  • prog (QProg) -- 目标量子程序。

  • quantum_machine (QuantumMachine) -- 量子计算机。

  • b_optimization (bool) -- 是否开启优化。

  • arch_matrix (numpy.ndarray[numpy.float64[m,n]]) -- 架构图矩阵。

返回:

映射后的量子程序。

返回类型:

QProg

示例用法:

# 使用初始映射和默认参数进行BMT映射
mapped_prog_default = OBMT_mapping(my_prog, my_quantum_machine, b_optimization=True)

# 使用自定义参数进行BMT映射
custom_max_partial = 100  # 自定义每步最大部分解数量
custom_max_children = 50   # 自定义每个双量子门的最大候选解数量
custom_config_data = 'my_config.json'  # 自定义配置数据文件路径
mapped_prog_custom = OBMT_mapping(my_prog, my_quantum_machine, b_optimization=True, max_partial=custom_max_partial, max_children=custom_max_children, config_data=custom_config_data)

# 使用初始映射和自定义拓扑结构矩阵进行BMT映射
custom_arch_matrix = numpy.array(...)  # 自定义拓扑结构矩阵
mapped_prog_custom_arch = OBMT_mapping(my_prog, my_quantum_machine, b_optimization=True, arch_matrix=custom_arch_matrix)

我们同样以上述的一维链和输入参数为例：

from pyqpanda import *
import numpy as np

if __name__ == "__main__":

    machine = CPUQVM()
    machine.init_qvm()

    q = machine.qAlloc_many(6)

    prog = QProg()
    prog << CNOT(q[0],q[5])<< CNOT(q[4],q[1])<< CNOT(q[3],q[0])<< CNOT(q[2],q[5])

    num_nodes = 6
    chain_graph = np.zeros((num_nodes, num_nodes), dtype=np.double)

    for i in range(num_nodes - 1):
        chain_graph[i, i + 1] = 1
        chain_graph[i + 1, i] = 1

    obmt_mapping_result = OBMT_mapping(prog,machine,True,chain_graph)

映射后的结果为：

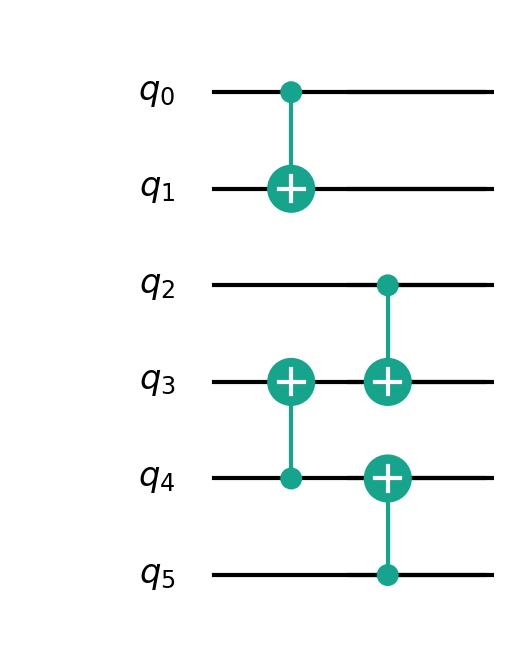
../_images/obmt_mapping.jpg

量子逻辑门分解

简介

量子逻辑门分解是指将一个复杂的量子逻辑门拆解成一系列基本的量子逻辑门的组合。在量子计算中，量子逻辑门是用于对量子比特进行操作和计算的基本单元。通过将复杂的逻辑门分解成基本的逻辑门，可以更容易地实现复杂的量子计算任务。量子逻辑门分解通常遵循一些特定的量子门集合，例如单量子比特门（如Hadamard门、相位门、旋转门等）和双量子比特门（如CNOT门、SWAP门等）。通过使用这些基本门，可以将任意的量子逻辑门拆解成一系列的基本门序列。 这个分解的过程类似于在经典计算中，将复杂的逻辑函数分解成基本的逻辑门（例如AND、OR、NOT等）的组合。量子逻辑门分解在量子算法设计、误差校正和量子编程中起着重要作用，因为它允许我们将复杂的问题分解成更易于实现和控制的部分。

CS 分解

Cosine-Sine Decomposition，我们称为CS分解，或者CSD。首先我们回顾以下在矩阵计算中的CS(Cosine-Sine)分解，在CS分解中，对于一个偶数维度的酉矩阵 \(U \in \mathbb{C}^{l\times l}\) 能被分解成更小的矩阵 \(A_1, A_2, B_1, B_2\) 和实数对角矩阵 \(C, S\) , 其中 \(C^2 + S^2 = I_{l/2}\)

\[\begin{split}\begin{aligned} U = \begin{pmatrix} A_1 & \\ & B_1 \end{pmatrix}\begin{pmatrix} C & -S \\ S & C \end{pmatrix}\begin{pmatrix} A_2 & \\ & B_2 \end{pmatrix} \end{aligned}\end{split}\]

对于一个矩阵U，左右两部分 \(A_j \oplus B_j\) 是由最重要的量子比特控制的量子多路器，它决定了 \(A_j, B_j\) 是否被应用到低位的比特上。中间部分与 \(R_y\) 门的结构相同, 仔细观察可以发现 对于低位比特的每一个经典配置，将 \(R_y\) 门应用在最有效位上。因此CS分解可以写成以下形式：

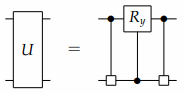
../_images/CS_1.png

对于多路CS分解，我们可以通过MEP(多路拓展特性)来增加更多的量子比特。 如下图所示。

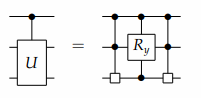
../_images/CS_2.png

代码示例

from pyqpanda import *
from scipy.stats import unitary_group

if __name__ == "__main__":
    machine = CPUQVM()
    machine.init_qvm()
    q = machine.qAlloc_many(3)
    c = machine.cAlloc_many(3)

    # 生成任意酉矩阵
    unitary_matrix = unitary_group.rvs(2**3,random_state=169384)

    # 输入需要被分解的线路
    prog = QProg()
    prog<<matrix_decompose(q,unitary_matrix,mode=DecompositionMode.CSDecomposition)
    draw_qprog(prog, "pic")
../_images/QCircuit_csd.jpg

QS 分解

QS(Quantum Shannon)分解中涉及到多路分解，对于一个多路分解，我们有：

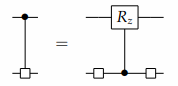
../_images/QS_1.png

令 \(U = U_0 \oplus U_1\) 为可选多路器，我们根据U的实现来设立并解决这个方程，让酉矩阵 \(V,W\) 和酉对角矩阵 \(D\) 满足 \(U = (I \otimes V)(D \oplus D^\dagger)(I \otimes W)\) ,或者写成：

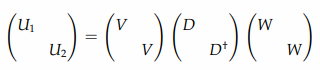
../_images/QS_3.png

将 \(U_1,U_2\) 相乘，消去含 \(W\) 的相关项，得到 \(U_1U_2^\dagger = VD^2V^\dagger\) 。我们能通过这个方程利用对角化从 \(U_1U_2^\dagger\) 中得到 \(D\) 和 \(V\) 。此外 \(W = DV^\dagger U_2\) 。 标记 \(D\) 的对角线，矩阵 \(D \oplus D^\dagger\) 在线路中对应 \(R_z\) 门。

利用新的分解，我们在CS分解中的两边的多路器在进行分解，就能得到递归应用的通用算符分解：

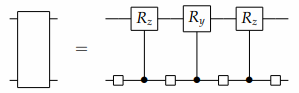
../_images/QS_2.png

因此，一个任意的n量子比特操作算子可以由三个复合R门和四个通用 \(n - 1\) 比特的操作算子来实现，这些算子可以被看作是原始算子的辅助因子。

代码示例

from pyqpanda import *
from scipy.stats import unitary_group

if __name__ == "__main__":
    machine = CPUQVM()
    machine.init_qvm()
    q = machine.qAlloc_many(3)
    c = machine.cAlloc_many(3)

    # 生成任意酉矩阵
    unitary_matrix = unitary_group.rvs(2**3,random_state=169384)

    # 输入需要被分解的线路
    prog = QProg()
    prog<<matrix_decompose(q,unitary_matrix,mode=DecompositionMode.QSDecomposition)
    draw_qprog(prog, "pic")
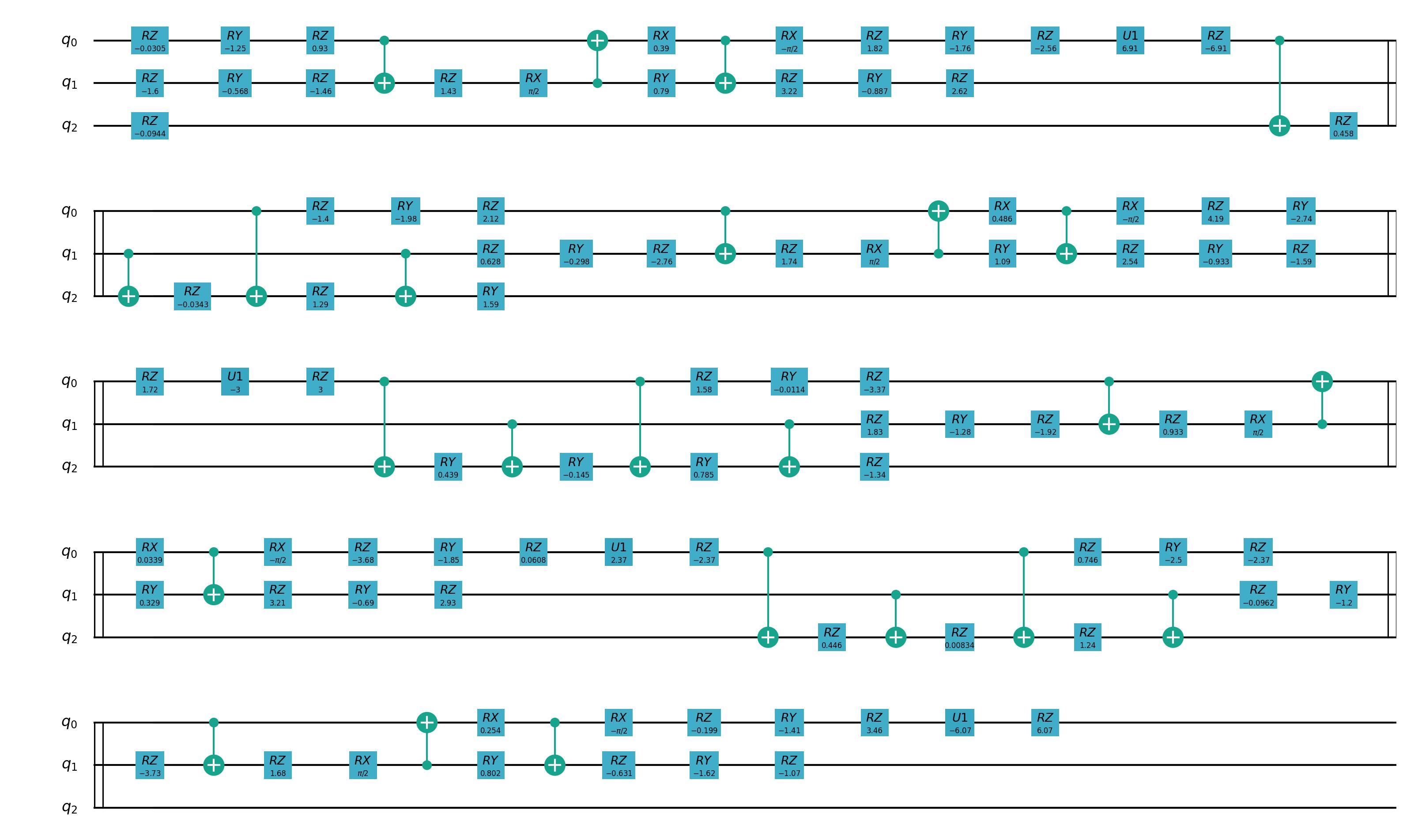
../_images/QCircuit_qsd.jpg

多控门分解

目前，由于量子计算的发展受到芯片的运行逻辑门集的限制，无法执行多比特量子逻辑门，因此针对多比特门，需要进行量子线路的重新表征。

而在多比特门中最为常用的则是多比特控制门，例如Grover算法中所需的数据索引空间表示，HHL算法中的uncompute模块的构建等

同时，为了使量子程序保真度达到所需阈值之上，降低线路深度则是一种有效的方法。

通常我们使用量子虚拟机来模拟多控门量子线路，对于某些量子虚拟机而言，含有多控门的量子线路通常线路深度较深，无法满足模拟要求，下图是一种常用的多控门分解方案，其中 \(V^4=U\)。

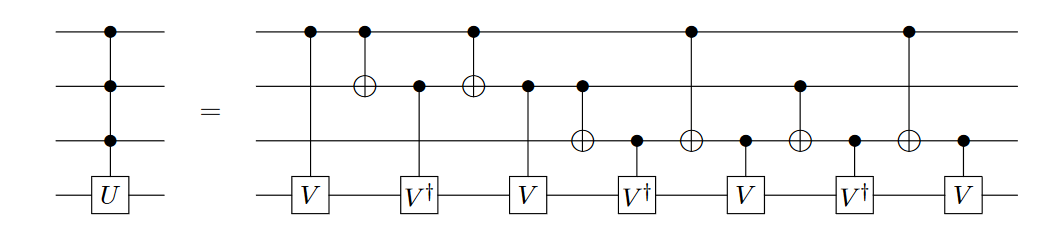
../_images/multi_control.png

不同的分解算法效果天差地别，量子线路的有效分解可以降低量子计算的时间和噪声产生的影响。而由于有噪声的影响，量子线路的大小就受到了限制；那么最小化量子线路的深度在实现量子算法起到 至关重要的作用。

分解方案的核心目的是提高量子线路分解的有效性，分解有效性的衡量标准有：

    1. 分解后量子线路的深度

    1. 分解的单量子逻辑门和双量子逻辑门的数量

    1. 是否需要辅助量子比特等

在更加复杂的量子算法场景下，将会出现更多的、受控维度更高的多控门。目前实现的物理量子计算机基本都不支持多控门，并且我们无法保证所有的受控物理qubit都处于连通状态（目前的物理量子芯片都有固定的拓扑结构），所以想要在真实物理量子计算机上运行量子算法，首先要对多控门进行拆解，使其转换成N个量子芯片支持的逻辑门的组合，以适配目标量子芯片。

方案细节

这里我们是用一种基于线性深度的多控门分解方案，其基本思想是，将控制位的数量逐次分解递减，多控门逐步分解为受控比特递减的多控门组合，然后这些多控门再一次递归分解，直到控制比特为1，

其中线性深度的含义是针对量子线路深度随量子比特线性增长的分解方案，而不是分解复杂度线性增加，得到的最终产物是多个单比特控制位单门集合，具体步骤如下：

  • 1. 对于任意符合n个控制比特的多控门，均可用如下形式表示

    \[\large C^{n}U=Q_{n}^{\dagger}P_n(U)^{\dagger}Q_{n}(a_1\sqrt[2^{n-1}]{U}a_{n+1})P_n(U)\]

    其中 \(a_jU_{a_k}\) 表示一个由单量子位控制的单门，控制比特是 \({a_j}\) ，目标比特是 \(a_k\) ，同时 \(C^{n}U\) 表示多量子位控制，控制比特是 \({a_1,···,a_n}\) ，目标比特是 \({a_{n+1}}\) 。

  • 2. 第一次分解会得到四个子式，相当于四个子量子线路或量子逻辑门，其中：

    \(\large Q_n=\prod_{k=1}^{n-1}C^kR_x(\pi)\)

    \(\large P_n(U)=\prod_{k=2}^na_k\sqrt[2^{n-k+1}]{U}a_{n+1}\)

    在上述式子中， \(\large P_n(U)\) 是多个单控制位量子逻辑门组合， \(\large Q_n\) 是控制位数量-1的多控门组合，具体地可以推导出，即每次分解后依然存在多控门，但是多控门的控制位数量递减，即

    \[\large Q_n=Q_{n-1}C^{n-1}R_x(\pi)\]

  • 3. 继续重复上述过程，知道控制比特为1

上述方案适用于所有单门受控比特情形，双量子逻辑门的控制场景下，可以先做进一步转化，转化为一个或多个多控制位的的单量子逻辑门集合，对于CNOT、CZ、CR、CU等，可以依次看作X、Z、U1、U4的单门控制形式，对于交换门，如SWAP，ISWAP和SQISWAP等，可以转化为上述支持的基础单双门组合。

多控门分解接口

ldd_decompose(qprog: QProg) → QProg

该函数用于分解多控制量子门，以得到一个新的量子程序，其中多控制量子门被分解成更基本的单比特和双比特门的序列。

参数:

qprog (QProg) -- 要进行分解的量子程序。

返回:

经过分解后的新量子程序。

返回类型:

QProg

我们以上图的四比特控制门为例，

from pyqpanda import *
import numpy as np

if __name__ == "__main__":
    machine = CPUQVM()
    machine.init_qvm()
    q = machine.qAlloc_many(4)
    c = machine.cAlloc_many(4)

    # 输入需要被分解的线路
    prog = QProg()
    prog << X(q[3]).control([q[0],q[1],q[2]])

    #执行多控门分解操作
    after_prog = ldd_decompose(prog)
    draw_qprog(after_prog, "pic")

可以得到分解的结果为：

../_images/multi_result.jpg