量子逻辑门

---

经典计算中，最基本的单元是比特，而最基本的控制模式是逻辑门。我们可以通过逻辑门的组合来达到我们控制电路的目的。类似地，处理量子比特的方式就是量子逻辑门。 使用量子逻辑门，我们有意识的使量子态发生演化。所以量子逻辑门是构成量子算法的基础。

量子逻辑门由酉矩阵表示。最常见的量子门在一个或两个量子位的空间上工作，就像常见的经典逻辑门在一个或两个位上操作一样。

单比特的门可以用以下形式表达：

\[\begin{aligned} |\psi\rangle=\alpha|0\rangle+\beta|1\rangle \end{aligned}\]

其中 \(\alpha\) 和 \(\beta\) 是复数，在测量中，比特出现在 \(|0\rangle\) 的概率是 \(|\alpha|^2\) ， \(|1\rangle\) 的概率是 \(|\beta|^2\) 。作为向量表示为：

\[\begin{split}\begin{aligned} |\psi\rangle=\left(\begin{array}{l}\alpha \\ \beta\end{array}\right) \end{aligned}\end{split}\]

由于概率守恒 \(|\alpha|^2+|\beta|^2=1\) ，并且因为无法检测到全局相位 \(|\psi\rangle:=e^{i\delta}|\psi\rangle\) 。 我们只需要两个实数就能描述单量子比特量子态。

一个便捷的表示方法是

\[\begin{aligned} |\psi\rangle=\cos(\theta/2)|0\rangle+\sin(\theta/2)e^{i\phi}|1\rangle \end{aligned}\]

其中 \(0\leq\phi<2\pi\) , \(0\leq\theta\leq\pi\) 。由此可见，在量子比特态和单位球面上的点之间存在一一对应关系，这就是量子比特态的布洛赫球表示法。

量子门通常用矩阵表示，作用于一个量子比特的门由一个 \(2\times2\) 单元矩阵表示，将表示门的矩阵与表示量子态的矢量相乘，就能得到量子门的功能。

\[\begin{aligned} |\psi^{\prime}\rangle=U|\psi\rangle \end{aligned}\]

一般酉矩阵能够使 \(|0\rangle\) 到上述状态。即

\[\begin{split}\begin{aligned} U=\begin{bmatrix} cos(\theta/2) & a \\ e^{i\phi}sin(\theta/2) & b \end{bmatrix}\quad \end{aligned}\end{split}\]

a和b是复数，其约束条件是： \(0\leq\theta\leq\pi\) 和 \(0\leq\phi<2\pi\) 对于所有的 \(U^\dagger U=I\) 。这样就会得到三个约束条件： \(a\to-e^{i\lambda}\sin(\theta/2), b\to e^{i\lambda+i\phi}\cos(\theta/2),\) 其中 \(0\leq\lambda<2\pi\) 。

\[\begin{split}\begin{aligned} U(\theta,\phi,\lambda)=\begin{pmatrix} cos\left(\frac\theta2\right) & -e^{i\lambda}\sin\left(\frac\theta2\right) \\ e^{i\phi}\sin\left(\frac\theta2\right) & e^{i(\phi+\lambda)}\cos\left(\frac\theta2\right)\end{pmatrix} \end{aligned}\end{split}\]

\[ \begin{align}\begin{aligned}\begin{aligned}\\\end{aligned}\end{aligned}\end{align} \]

常见量子逻辑门矩阵形式

单比特量子逻辑门

I门

又称为Id门或者Identity门。I门没有任何作用，适用于任何量子线路的任意地方。

这个门主要有两个使用途径：

1. 一个是在计算的时候经常使用。比如在证明两个门的矩阵是互逆矩阵的时候经常用到；

2. 在讨论实际的硬件操作时，“没有作用”等价于“无操作”。

I

\(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\quad\)

---

Phase门

P

\(\begin{bmatrix} 1 & 0 \\ 0 & e^{i\theta} \end{bmatrix}\quad\)

P门，又称为相位门，是可以设置参数的门。需要向其输入正确的数字（ \(\theta\) ）。 P门是以Z轴为基准，旋转 \(\theta\) 。

\[\begin{aligned} p(\lambda)= U(0, 0, \lambda) \end{aligned}\]

---

Hadamard门

常用来对单一量子比特做基地变换，同时产生产生叠加态。

\[\begin{split}\begin{aligned} H = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1\\ 1 & -1 \end{pmatrix}= U(\pi/2,0,\pi) \end{aligned}\end{split}\]

Hadamard

\(\begin{bmatrix} 1/\sqrt {2} & 1/\sqrt {2} \\ 1/\sqrt {2} & -1/\sqrt {2} \end{bmatrix}\quad\)

---

X门的作用是将状态0和1的振幅进行转换。

\[\begin{split}\begin{aligned} X &= \begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}= U(\pi,0,\pi) \end{aligned}\end{split}\]

Y门的作用是在Bloch球中以y轴为中心旋转 \(\pi\) 。

\[\begin{split}\begin{aligned} Y &= \begin{pmatrix} 0 & -i\\ i & 0 \end{pmatrix}=U(\pi,\pi/2,\pi/2) \end{aligned}\end{split}\]

Z门的作用是在Bloch球中以z轴为中心旋转 \(\pi\) 。

\[\begin{split}\begin{aligned} Z &= \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}=P(\pi) \end{aligned}\end{split}\]

	Pauli-X	\(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\quad\)
	Pauli-Y	\(\begin{bmatrix} 0 & -1i \\ 1i & 0 \end{bmatrix}\quad\)
	Pauli-Z	\(\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\quad\)

	X1	\(\begin{bmatrix} 1/\sqrt {2} & -1i/\sqrt {2} \\ -1i/\sqrt {2} & 1/\sqrt {2} \end{bmatrix}\quad\)
	Y1	\(\begin{bmatrix} 1/\sqrt {2} & -1/\sqrt {2} \\ 1/\sqrt {2} & 1/\sqrt {2} \end{bmatrix}\quad\)
	Z1	\(\begin{bmatrix} e^{-i\pi/4} & 0 \\ 0 & e^{i\pi/4} \end{bmatrix}\quad\)

\[\begin{split}\begin{aligned} R_x(\theta) = \begin{pmatrix} \cos(\theta/2) & -i\sin(\theta/2)\\ -i\sin(\theta/2) & \cos(\theta/2) \end{pmatrix} = U(\theta, -\pi/2,\pi/2) \end{aligned}\end{split}\]

\[\begin{split}\begin{aligned} R_y(\theta) = \begin{pmatrix} \cos(\theta/2) & - \sin(\theta/2)\\ \sin(\theta/2) & \cos(\theta/2) \end{pmatrix} =U(\theta,0,0) \end{aligned}\end{split}\]

\[\begin{split}\begin{aligned} R_z(\phi) = \begin{pmatrix} e^{-i \phi/2} & 0 \\ 0 & e^{i \phi/2} \end{pmatrix}\equiv P(\phi) \end{aligned}\end{split}\]

	RX	\(\begin{bmatrix} \cos(\theta/2) & -1i×\sin(\theta/2) \\ -1i×\sin(\theta/2) & \cos(\theta/2) \end{bmatrix}\quad\)
	RY	\(\begin{bmatrix} \cos(\theta/2) & -\sin(\theta/2) \\ \sin(\theta/2) & \cos(\theta/2) \end{bmatrix}\quad\)
	RZ	\(\begin{bmatrix} e^{-i\theta/2} & 0 \\ 0 & e^{i\theta/2} \end{bmatrix}\quad\)

---

T，S门

T门作为经常使用的门，是 \(\theta = \pi/4 的P门。在Bloch球中，绕z轴旋转\pi/4\) 。

\[\begin{split}\begin{aligned} T = \begin{pmatrix} 1 & 0\\ 0 & i \end{pmatrix}= P(\pi/4) \end{aligned}\end{split}\]

\[\begin{split}\begin{aligned} T^{\dagger} = \begin{pmatrix} 1 & 0\\ 0 & -i \end{pmatrix}= P(-\pi/4) \end{aligned}\end{split}\]

S门也是P门的一种情况，为 \(\theta = \pi/2\) 的P门。在Bloch球中，绕z轴旋转 \(\pi/2\) 。

\[\begin{split}\begin{aligned} S = \begin{pmatrix} 1 & 0\\ 0 & i \end{pmatrix}= P(\pi/2) \end{aligned}\end{split}\]

\[\begin{split}\begin{aligned} S^{\dagger} = \begin{pmatrix} 1 & 0\\ 0 & -i \end{pmatrix}= P(-\pi/2) \end{aligned}\end{split}\]

	T	\(\begin{bmatrix} 1 & 0 \\ 0 & e^{i\pi / 4} \end{bmatrix}\quad\)
	S	\(\begin{bmatrix} 1 & 0 \\ 0 & e^{i\pi / 2} \end{bmatrix}\quad\)

---

U门

上述很多门都是P门的特殊情况，而在所有单一比特的量子门中最为常见的是 \(U_3\) 门。 本章所有的门都可以通过调整 \(U_3\) 门的参数来实现。

\[\begin{split}\begin{aligned} U(\theta, \phi, \lambda) = \begin{pmatrix} \cos\left(\frac{\theta}{2}\right) & -e^{i\lambda}\sin\left(\frac{\theta}{2}\right) \\ e^{i\phi}\sin\left(\frac{\theta}{2}\right) & e^{i(\phi+\lambda)}\cos\left(\frac{\theta}{2}\right) \end{pmatrix} \end{aligned}\end{split}\]

在pyqpanda中也可以直接通过使用 \(U_1, U_2, U_3, U_4\) 。来调用相关量子门。

\[\begin{split}\begin{aligned} U1(\lambda) &= P(\lambda) = U(0, 0, \lambda) \\ U2(\phi, \lambda) &= U(\frac{\pi}{2}, \phi, \lambda)\\ U3(\theta, \phi, \lambda) &= U(\theta, \phi, \lambda)\\ U4(\alpha, \beta, \gamma, \delta) &= e^{-i*(\alpha+(\beta+\delta)/2)}U3(\gamma, \delta, \lambda) \end{aligned}\end{split}\]

	U1	\(\begin{bmatrix} 1 & 0 \\ 0 & e^{i\theta} \end{bmatrix}\quad\)
	U2	\(\begin{bmatrix} 1/\sqrt {2} & -e^{i\lambda}/\sqrt {2} \\ e^{i\phi}/\sqrt {2} & e^{i\lambda+i\phi}/\sqrt {2} \end{bmatrix}\quad\)
	U3	\(\begin{bmatrix} \cos(\theta/2) & -e^{i\lambda}\sin(\theta/2) \\ e^{i\phi}\sin(\theta/2) & e^{i\lambda+i\phi}\cos(\theta/2) \end{bmatrix}\quad\)
	U4	\(\begin{bmatrix} e^{i*(\alpha-(\beta+\delta)/2)}*cos(\gamma/2) & -e^{i*(\alpha-(\beta-\delta)/2)}*sin(\gamma/2) \\ e^{i*(\alpha+(\beta-\delta)/2)}*sin(\gamma/2) & e^{i*(\alpha+(\beta+\delta)/2)}*cos(\gamma/2) \end{bmatrix}\quad\)

---

RPhi门

在NISQ时代，量子计算机无法做到任意逻辑门的运行。因此需要将其转化为量子芯片所支持的基础逻辑门集合以实现通用计算。在本源量子芯片中所支持的单双门组合则为 \(U_3\) 和 \(CZ\) 。因此，在编译量子程序时，QPanda会对非基础逻辑门进行转换，转换方法如下所示。

首先，定义 \(\phi\) 为 \(XY`\) 平面内某一旋转轴与 \(X\) 正向的夹角，则对任意 \(XY\) 旋转门，有：

\[\begin{split}\begin{aligned} R_\phi(\theta) = cos\frac{\theta}{2}I - i sin\frac{\theta}{2}(cos\phi\sigma_x + sin\phi\sigma_y) = \begin{bmatrix} cos\frac{\theta}{2} & -i sin\frac{\theta}{2}e^{-i\phi} \\ -isin\frac{\theta}{2}e^{i\phi} & cos\frac{\theta}{2} \end{bmatrix} \end{aligned}\end{split}\]

Z旋转门的形式如下：

\[\begin{split}\begin{aligned} RZ(\theta) = cos\frac{\theta}{2}I - i sin\frac{\theta}{2}\sigma_Z = \begin{bmatrix} 1 & 0 \\ 0 & e^{i\theta} \end{bmatrix} \end{aligned}\end{split}\]

易证：

\[\begin{split}\begin{aligned} \begin{split} RX(\theta_X)RZ(\theta_Z) = RZ(\theta_Z)R_{-\theta_Z}(\theta_X) \\ RZ(\theta_{Z2})RZ(\theta_{Z1}) = RZ(\theta_{Z1} + \theta_{Z2}) \\ CZ[RZ(\theta_{Z1}) \otimes RZ(\theta_{Z2})] = [RZ(\theta_{Z1}) \otimes RZ(\theta_{Z2}) ]·CZ \end{split} \end{aligned}\end{split}\]

以上公式是Virtual Z 门的基础。它意味着，可以将线路中已有的Z操作转移到XY操作之后，作为替代，原XY操作的旋转轴将随之变换。而被转移到线路后排的Z操作可以合并，并继续转移，以此类推。

多比特量子逻辑门

量子计算机的空间随着量子比特的数量呈指数增长。对于 n 个量子比特，复向量空间的维数为 \(d=2^n\) 。为了描述多量子比特系统的状态，张量积被用来 "粘合 "算子和基向量。

让我们先考虑一个双量子比特系统。给定两个分别作用于一个量子比特的算子 A 和 B，那么作用于两个量子比特的联合算子 \(A\otimes B\) .

\[\begin{split}\begin{aligned} A\otimes B=\begin{pmatrix}A_{00}\begin{pmatrix}B_{00}&B_{01}\\B_{10}&B_{11}\end{pmatrix}&A_{01}\begin{pmatrix}B_{00}&B_{01}\\B_{10}&B_{11}\end{pmatrix}\\A_{10}\begin{pmatrix}B_{00}&B_{01}\\B_{10}&B_{11}\end{pmatrix}&A_{11}\begin{pmatrix}B_{00}&B_{01}\\B_{10}&B_{11}\end{pmatrix}\end{pmatrix} \end{aligned}\end{split}\]

其中， \(A_{jk} 和 B_{lm}\) 分别是A和B的矩阵元素。

与此类似，双量子比特系统的基向量也是通过单量子比特基向量的张量乘积形成的：

\[\begin{split}\begin{aligned} |00\rangle=\begin{pmatrix}1\begin{pmatrix}1\\0\end{pmatrix}\\0\begin{pmatrix}1\\0\end{pmatrix}\end{pmatrix}=\begin{pmatrix}1\\0\\0\\0\end{pmatrix}\quad|01\rangle=\begin{pmatrix}1\begin{pmatrix}0\\1\end{pmatrix}\\0\begin{pmatrix}0\\1\end{pmatrix}\end{pmatrix}=\begin{pmatrix}0\\1\\0\\0\end{pmatrix} \end{aligned}\end{split}\]

\[\begin{split}\begin{aligned} |10\rangle=\begin{pmatrix}0\begin{pmatrix}1\\0\end{pmatrix}\\1\begin{pmatrix}1\\0\end{pmatrix}\end{pmatrix}=\begin{pmatrix}0\\0\\1\\0\end{pmatrix}\quad|11\rangle=\begin{pmatrix}0\begin{pmatrix}0\\1\end{pmatrix}\\1\begin{pmatrix}0\\1\end{pmatrix}\end{pmatrix}=\begin{pmatrix}0\\0\\0\\1\end{pmatrix} \end{aligned}\end{split}\]

注意，我们为基向量的张量乘引入了一个简写 \(|0\rangle\otimes|0\rangle\) 记作 \(\left|00\right\rangle\) 。n 量子比特系统的状态可以用n维量子比特基向量的张量积来描述。请注意，2量子比特系统的基向量是4维的；如前所述，一般来说，n量子比特系统的基向量是 \(2^n\) 维的。

大多数双量子比特门都属于受控类型（SWAP 门是个例外）。一般来说，受控双量子比特门 \(C_U\) 的作用是，当第一个量子比特的状态处于 \(|1\rangle\) 时，将单量子比特单元应用于第二个量子比特U。假设有一个矩阵U表示

\[\begin{split}\begin{aligned} U=\begin{pmatrix}u_{00}&u_{01}\\u_{10}&u_{11}\end{pmatrix}. \end{aligned}\end{split}\]

我们可以计算出 \(C_U\) 的作用如下。回顾一下，双量子比特系统的基向量排序为 \(|00\rangle,|01\rangle,|10\rangle,|11\rangle\) 。假设控制量子比特是量子比特 \(q_0\) 。如果控制量子比特是 \(|1\rangle\) 的情况下，U则应作用于目标位。因此，在 \(C_U\) 的作用下，基向量会根据以下公式进行变换

\[\begin{aligned} C_{U}: \underset{\text{qubit}~1}{\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|0\right\rangle} &\rightarrow \underset{\text{qubit}~1}{\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|0\right\rangle} \end{aligned}\]

\[\begin{aligned} C_{U}: \underset{\text{qubit}~1}{\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|1\right\rangle} &\rightarrow \underset{\text{qubit}~1}{\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|1\right\rangle} \end{aligned}\]

\[\begin{aligned} C_{U}: \underset{\text{qubit}~1}{\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{\left|0\right\rangle} &\rightarrow \underset{\text{qubit}~1}{\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{U\left|0\right\rangle} \end{aligned}\]

\[\begin{aligned} C_{U}: \underset{\text{qubit}~1}{\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{\left|1\right\rangle} &\rightarrow \underset{\text{qubit}~1}{\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{U\left|1\right\rangle} \end{aligned}\]

\(C_U\) 的矩阵形式为:

\[\begin{split}\begin{aligned} \begin{aligned} C_U = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & u_{00} & u_{01} \\ 0 & 0 & u_{10} & u_{11} \end{pmatrix} \end{aligned} \end{aligned}\end{split}\]

其中，右下角对应酉矩阵形式为上述U4门：

CU

\(\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & u_{00} & u_{01} \\ 0 & 0 & u_{10} & u_{11} \end{bmatrix}\quad\)

---

CNOT门

作用于两个量子比特的量子门，当第一个量子比特（控制位）为 |1⟩的时候，对第二个量子比特施加一个X门的效果。 所以CNOT在很多文献中也称为CX门。

CNOT

\(\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix}\quad\)

---

CZ门

如果控制量子比特是 |1⟩的时候，受控 Z 门会翻转目标量子比特的相位。无论控制量子位是 MSB 还是 LSB，矩阵看起来都是一样的：

\[\begin{split}\begin{aligned} C_Z = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & -1 \end{pmatrix} \end{aligned}\end{split}\]

CZ

\(\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \end{bmatrix}\quad\)

---

SWAP门

SWAP 门交换两个量子比特。它将基向量变换为

\[\begin{aligned} \left|00\right\rangle \rightarrow \left|00\right\rangle~,~\left|01\right\rangle \rightarrow \left|10\right\rangle~,~\left|10\right\rangle \rightarrow \left|01\right\rangle~,~\left|11\right\rangle \rightarrow \left|11\right\rangle \end{aligned}\]

SWAP

\(\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\quad\)

---

受控相位旋转CR门

如果两个量子比特都处于 \(\left|11\right\rangle\) 状态，则进行相位旋转。无论控制比特是 MSB 还是 LSB，矩阵看起来都是一样的。

CR

\(\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & e^{i\theta} \end{bmatrix}\quad\)

---

	iSWAP	\(\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & i & 0 \\ 0 & i & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\quad\)
	RXX	\(\begin{bmatrix} \cos(\theta/2) & 0 & 0 & -i\sin(\theta/2) \\ 0 & \cos(\theta/2) & -i\sin(\theta/2) & 0 \\ 0 & -i\sin(\theta/2) & \cos(\theta/2) & 0 \\ -i\sin(\theta/2) & 0 & 0 & \cos(\theta/2) \end{bmatrix}\quad\)
	RYY	\(\begin{bmatrix} \cos(\theta/2) & 0 & 0 & i\sin(\theta/2) \\ 0 & \cos(\theta/2) & -i\sin(\theta/2) & 0 \\ 0 & -i\sin(\theta/2) & \cos(\theta/2) & 0 \\ i\sin(\theta/2) & 0 & 0 & \cos(\theta/2) \end{bmatrix}\quad\)
	RZZ	\(\begin{bmatrix} e^{-i\theta/2} & 0 & 0 & 0 \\ 0 & e^{i\theta/2} & 0 & 0 \\ 0 & 0 & e^{i\theta/2} & 0 \\ 0 & 0 & 0 & e^{-i\theta/2} \end{bmatrix}\quad\)
	RZX	\(\begin{bmatrix} \cos(\theta/2) & 0 & -i\sin(\theta/2) & 0 \\ 0 & \cos(\theta/2) & 0 & i\sin(\theta/2) \\ -i\sin(\theta/2) & 0 & \cos(\theta/2) & 0 \\ 0 & i\sin(\theta/2) & 0 & \cos(\theta/2) \end{bmatrix}\quad\)

---

Toffoli门

如果前两个量子位都是 \(\left|1\right\rangle\) ，托福利门就会翻转第三个量子位。

\[\begin{aligned} |abc\rangle\to|bc\oplus a\rangle\otimes|b\rangle\otimes|c\rangle. \end{aligned}\]

Toffoli

\(\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ \end{bmatrix}\quad\)

---

QPanda 2把所有的量子逻辑门封装为API向用户提供使用，并可获得QGate类型的返回值。比如，您想要使用Hadamard门，就可以通过如下方式获得：

from pyqpanda import *
import numpy as np
qvm = CPUQVM()
qvm.init_qvm()
qubits = qvm.qAlloc_many(4)
h = H(qubits[0])

其中参数为目标比特，返回值为量子逻辑门

pyqpanda中支持的不含角度的单门有： I、 H、 T、 S、 X、 Y、 Z、 X1、 Y1、 Z1

qubit如何申请会在 GPU量子虚拟机 部分介绍。

单门带有一个旋转角的逻辑门，例如RX门：

rx = RX(qubits[0], np.pi/3)

第一个参数为目标比特，第二个参数为旋转角度

pyqpanda中支持的单门带有一个旋转角度的逻辑门有： RX、RY、RZ、U1、P

pyqpanda中还支持 U2、U3、U4 门，其用法如下：

# U2(qubit, phi, lambda) 有两个角度
u2 = U2(qubits[0], np.pi, np.pi/2)

# U3(qubit, theta, phi, lambda) 有三个角度
u3 = U3(qubits[0], np.pi, np.pi/2, np.pi/4)

# U4(qubit, alpha, beta, gamma, delta) 有四个角度
u4 = U4(qubits[0], np.pi, np.pi/2, np.pi/4, np.pi/2)

两比特量子逻辑门的使用和单比特量子逻辑门的用法相似，只不过是输入的参数不同，例如CNOT门：

cnot = CNOT(qubits[0], qubits[1])

第一个参数为控制比特 第二个参数为目标比特 注：两个比特不能相同

pyqpanda中支持的双门不含角度的逻辑门有： CNOT、CZ 、SWAP、iSWAp、SqiSWAP

双门带有旋转角度的门有：CR、RXX 、RYY、RZZ、RZX，例如CR门：

cr = CR(qubits[0], qubits[1], np.pi)

第一个参数为控制比特, 第二个参数为目标比特, 第三个参数为旋转角度

支持CU门，使用方法如下：

# CU(control, target, alpha, beta, gamma, delta) 有四个角度
cu = CU(qubits[0], qubits[1], np.pi, np.pi/2, np.pi/3, np.pi/4)

获得三量子逻辑门 Toffoli 的方式：

toffoli = Toffoli(qubits[0], qubits[1], qubits[2])

三比特量子逻辑门Toffoli实际上是CCNOT门，前两个参数是控制比特，最后一个参数是目标比特。

接口介绍

在本章的开头介绍过，所有的量子逻辑门都是酉矩阵，那么您也可以对量子逻辑门做转置共轭操作，获得一个量子逻辑门 dagger 之后的量子逻辑门可以用下面的方法：

rx_dagger = RX(qubits[0], np.pi).dagger()

或：

rx_dagger = RX(qubits[0], np.pi)
rx_dagger.set_dagger(True)

也可以为量子逻辑门添加控制比特,获得一个量子逻辑门 control 之后的量子逻辑门可以用下面的方法：

qvec = [qubits[0], qubits[1]]
rx_control = RX(qubits[2], np.pi).control(qvec)

或：

qvec = [qubits[0], qubits[1]]
rx_control = RX(qubits[2], np.pi)
rx_control.set_control(qvec)

pyqpanda 还封装了一些比较方便的接口，会简化一些量子逻辑门的操作。

单门操作：

cir = H(qubits)
print(cir)

          ┌─┐
q_0:  |0>─┤H├
          ├─┤
q_1:  |0>─┤H├
          ├─┤
q_2:  |0>─┤H├
          ├─┤
q_3:  |0>─┤H├
          └─┘

对多个量子比特添加H门

双门操作：

cir = CNOT(qubits[0:3], qubits[1:4])
print(cir)

q_0:  |0>────■── ────── ──────
          ┌──┴─┐
q_1:  |0>─┤CNOT├ ───■── ──────
          └────┘ ┌──┴─┐
q_2:  |0>─────── ┤CNOT├ ───■──
                 └────┘ ┌──┴─┐
q_3:  |0>─────── ────── ┤CNOT├
                        └────┘

对多个量子比特添加CNOT门

pyqpanda 还封装了自定义的QOracle逻辑门，通过传入一个由酉矩阵和对应的比特来构建一个QOracle逻辑门。

from pyqpanda import *

if __name__ == "__main__":
    qvm = CPUQVM()
    qvm.init_qvm()
    qubits = qvm.qAlloc_many(3)
    prog1 = QProg()
    prog1 <<H(qubits[0]) <<CNOT(qubits[1],qubits[2])
    mat = get_matrix(prog1,True)
    prog = QProg()
    prog << QOracle([qubits[0],qubits[1],qubits[2]],mat)

    res1 = qvm.prob_run_dict(prog1,qubits)
    res2 = qvm.prob_run_dict(prog,qubits)

    # 打印测量结果
    print(res1)
    print(res2)

计算结果如下：

{'000': 0.5000000000000001, '001': 0.5000000000000001, '010': 0.0, '011': 0.0, '100': 0.0, '101': 0.0, '110': 0.0, '111': 0.0}
{'000': 0.4999999999999999, '001': 0.4999999999999999, '010': 0.0, '011': 0.0, '100': 0.0, '101': 0.0, '110': 0.0, '111': 0.0}

实例

以下实例主要是向您展现QGate类型接口的使用方式。

from pyqpanda import *

if __name__ == "__main__":
   qvm = CPUQVM()
   qvm.init_qvm()
   qubits = qvm.qAlloc_many(3)
   control_qubits = [qubits[0], qubits[1]]
   prog = QProg()

   # 构建量子程序
   prog << apply_QGate([qubits[0], qubits[1]], H) \
         << H(qubits[0]).dagger() \
         << X(qubits[2]).control(control_qubits)

   # 对量子程序进行概率测量
   result = qvm.prob_run_dict(prog, qubits, -1)

   # 打印测量结果
   print(result)

计算结果如下：

{'000': 0.4999999999999894, '001': 0.0, '010': 0.4999999999999894, '011': 0.0, '100': 0.0, '101': 0.0, '110': 0.0, '111': 0.0}

量子线路

---

量子线路是量子计算领域中的一种重要模型，用于描述和研究量子算法和量子计算机的运行过程。它是一种图形化的表示方法，用于展示量子比特之间的操作和相互作用，类似于经典计算中的电路图。

由于组成量子线路的每一个量子逻辑门都是一个 酉算子 ，所以整个量子线路整体也是一个大的酉算子。

量子线路的主要目的是模拟和探究量子计算过程，通过在量子比特上应用各种量子门操作（如Hadamard门、CNOT门等），以实现复杂的量子算法，一般来说，量子线路的结构大致如下图所示：

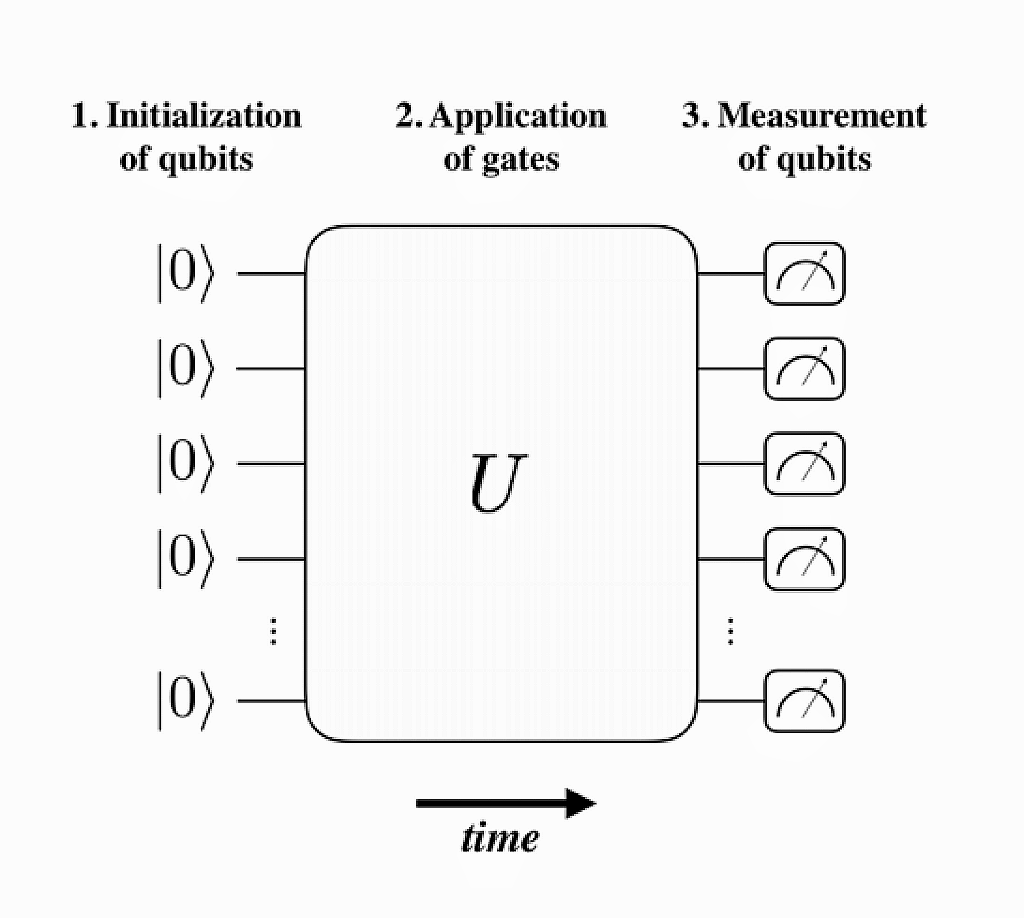
根据上图以及《量子计算与量子信息》一书的内容，量子线路的结构组成主要包括：

• 量子比特（Qubits） ：量子线路的基本单元，与经典计算中的比特类似，但具有量子叠加和纠缠等量子特性。

• 量子操作和量子门（Quantum Gates） ：这些是对量子比特进行操作的基本元素，类似于经典计算中的逻辑门。量子门可以是单比特门（只作用于一个量子比特）或多比特门（作用于多个量子比特），常见的有Hadamard门、Pauli门、CNOT门等。

• 时间线 ：即连接量子操作的线，表示执行时序，同时量子线路中量子门的顺序和连接方式形成了一种拓扑结构，该结构决定了量子算法的运行流程。

class QCircuit

该类实现了用于构建和操作量子线路的方法，通过添加量子门和控制操作等来生成量子线路。

__init__()

创建一个空的量子线路。

__init__(arg0: NodeIter)

根据给定的节点迭代器创建量子线路。

参数:

arg0 (NodeIter) -- 节点迭代器。

control(control_qubits: QVec) → QCircuit

获得QCircuit的施加控制之后的量子线路

参数:

control_qubits (QVec) -- 控制比特列表。

返回:

新的施加控制后的量子线路。

返回类型:

QCircuit

dagger() → QCircuit

获得QCircuit的转置共轭之后的量子线路

返回:

QCircuit的转置共轭之后的量子线路

返回类型:

QCircuit

insert(arg0: QCircuit) → QCircuit

:: insert(arg0: QGate) -> QCircuit

参数:

arg0 (QGate、QCircuit) -- 要插入的量子门和量子线路。

返回:

当前量子线路。

返回类型:

QCircuit

is_empty() → bool

检查量子线路是否为空。

返回:

若量子线路为空则为 True，否则为 False。

返回类型:

bool

set_control(control_qubits: QVec) → None

设置控制比特，用于实现控制门操作。

参数:

control_qubits (QVec) -- 控制比特列表。

set_dagger(arg0: bool) → None

设置线路是否为dagger形式。

参数:

arg0 (bool) -- 若为 True 则表示将线路设置为dagger

__lshift__(arg0: QCircuit) → QCircuit

:: __lshift__(arg0: QGate) -> QCircuit

参数:

arg0 (QGate、QCircuit) -- 通过左移操作符待插入的节点

返回:

生成的新量子线路。

返回类型:

QCircuit

在pyqpanda中，QCircuit类是一个仅装载量子逻辑门的容器类型，它也是QNode中的一种，初始化一个QCircuit对象除了上述直接使用初始化函数外，

cir = QCircuit()

还可以使用

prog = create_empty_circuit()

你可以通过如下方式向QCircuit尾部填充节点，在这里pyqpanda重载了 << 运算符作为插入量子线路的方法

cir << node

node的类型可以为QGate或QCircuit。

我们还可以获得QCircuit的转置共轭之后的量子线路，使用方式为：

cir_dagger = cir.dagger()

如果想复制当前的量子线路，并给复制的量子线路添加控制比特，可以使用下面的方式：

qvec = [qubits[0], qubits[1]]
cir_control = cir.control(qvec)

备注

• 向QCircuit中插入QPorg，QIf，Measure不会报错，但是运行过程中可能会产生预料之外的错误

• 一个构建好的QCircuit不能直接参与量子计算与模拟，需要进一步构建成QProg类型

from pyqpanda import *

if __name__ == "__main__":

    qvm = CPUQVM()
    qvm.init_qvm()
    qubits = qvm.qAlloc_many(4)
    cbits = qvm.cAlloc_many(4)

    # 构建量子程序
    prog = QProg()
    circuit = QCircuit()

    circuit << H(qubits[0]) \
            << CNOT(qubits[0], qubits[1]) \
            << CNOT(qubits[1], qubits[2]) \
            << CNOT(qubits[2], qubits[3])

    prog << circuit << Measure(qubits[0], cbits[0])

    # 量子程序运行1000次，并返回测量结果
    result = qvm.run_with_configuration(prog, cbits, 1000)

    # 打印量子态在量子程序多次运行结果中出现的次数
    print(result)

运行结果：

{'0000': 486, '0001': 514}

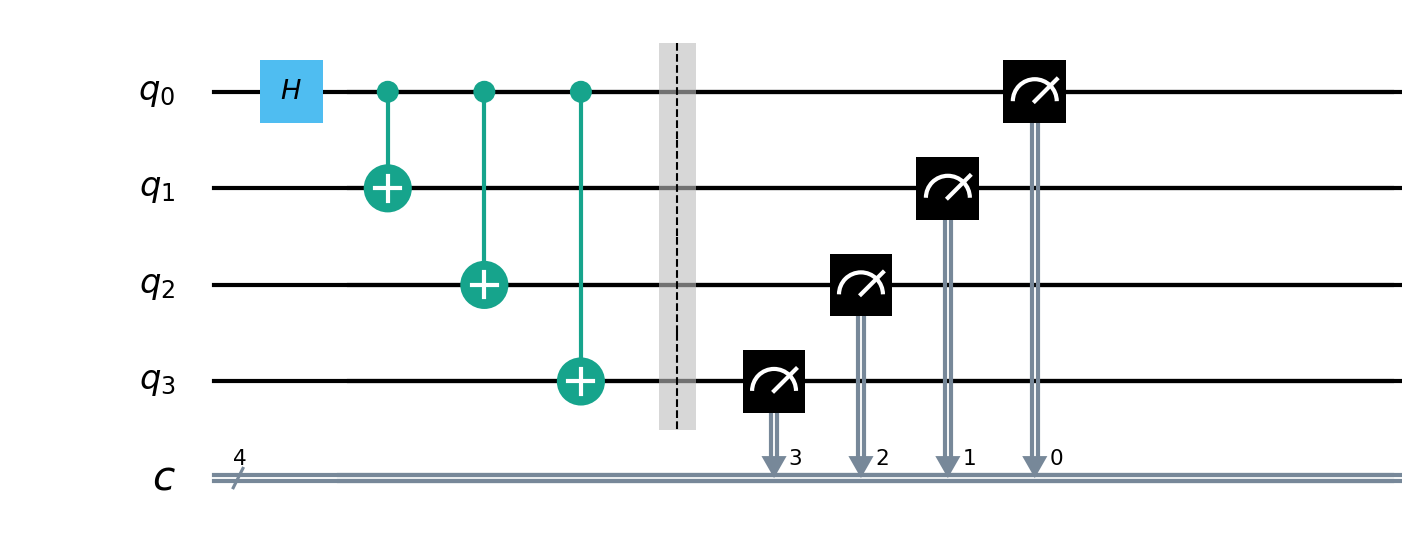
通过对申请的寄存器中中添加量子门，来设计量子线路，下图是通过添加H门和CNOT门来实现GHZ态。

在qubit0上添加H门，使其变成叠加态 \(\left(|0\rangle+|1\rangle\right)/\sqrt{2}\) 。

在qubit0和qubit1，2，3之间分别添加一个CNOT门，在理想的量子计算机上，构成的线路运行之后产生的状态就是GHZ态。

\[\begin{aligned} |\psi\rangle = \left(|0000\rangle+|1111\rangle\right)/\sqrt{2} \end{aligned}\]

\[\begin{aligned} \left(|0\rangle+|1\rangle\right)/\sqrt{2} \end{aligned}\]

from pyqpanda import *

if __name__ == "__main__":

    qvm = CPUQVM()
    qvm.init_qvm()
    qubits = qvm.qAlloc_many(4)
    cbits = qvm.cAlloc_many(4)

    # 构建量子程序
    prog = QProg()

    measure_node = Measure(qubits[0], cbits[0])

    或

    measure_node = Measure(0, 1)

量子程序

---

量子程序是一种描述量子计算任务的指令序列，类似于经典计算中的计算机程序。然而，与经典计算不同的是，量子程序在量子比特上执行操作，利用量子力学的奇特性质来进行信息处理。

在传统计算中，经典比特（0和1）是计算的基本单位，而在量子计算中，量子比特（或称为量子位）可以同时处于0和1的叠加态，还可以通过纠缠现象与其他量子比特相互关联。这些量子特性赋予了量子程序强大的计算能力，使其能够解决一些经典计算难题，如因子分解和优化问题。

量子程序的核心是量子门操作，它们是对量子比特进行操作的基本构建块。通过使用不同的量子门操作，可以在量子比特之间创建复杂的量子态和量子纠缠，实现量子计算中的各种算法和任务。量子程序还包括测量操作，将量子信息转化为经典信息以便进一步分析和处理。

编写和优化量子程序是量子计算研究和应用的关键一步。设计合理的量子门序列、选择适当的量子比特布局以及优化操作顺序等都会影响量子程序的执行效率和准确性。随着量子计算技术的不断发展，量子程序成为了探索量子算法、量子模拟、量子优化等领域的重要工具。

在QPanda2中，QProg是量子编程的一个容器类，是一个量子程序的最高单位。

class QProg

该类实现了量子程序的构建，使用链表数据结构存储量子电路。可用于构建量子电路，执行量子操作以及进行分析。

__init__()

初始化一个空的量子程序。

__init__(prog: QProg)

使用另一个量子程序构造新的量子程序节点。

参数:

prog (QProg) -- 要复制的量子程序。

返回:

一个新的量子程序节点。

__init__(qcircuit: QCircuit)

使用一个量子线路构造新的量子程序节点。

参数:

qcircuit (QCircuit) -- 要转换为量子程序的量子线路。

返回:

一个新的量子程序节点。

__init__(qif_prog: QIfProg)

使用一个 QIfProg 节点构造新的量子程序节点。

参数:

qif_prog (QIfProg) -- 要转换为量子程序的 QIfProg 节点。

返回:

一个新的量子程序节点。

__init__(qwhile_prog: QWhileProg)

使用一个 QWhileProg 节点构造新的量子程序节点。

参数:

qwhile_prog (QWhileProg) -- 要转换为量子程序的 QWhileProg 节点。

返回:

一个新的量子程序节点。

__init__(qgate: QGate)

使用一个 QGate 节点构造新的量子程序节点。

参数:

qgate (QGate) -- 要转换为量子程序的 QGate 节点。

返回:

一个新的量子程序节点。

__init__(qmeasure: QMeasure)

使用一个 QMeasure 节点构造新的量子程序节点。

参数:

qmeasure (QMeasure) -- 要转换为量子程序的 QMeasure 节点。

返回:

一个新的量子程序节点。

__init__(qreset: QReset)

使用一个 QReset 节点构造新的量子程序节点。

参数:

qreset (QReset) -- 要转换为量子程序的 QReset 节点。

返回:

一个新的量子程序节点。

__init__(cc: ClassicalCondition)

使用一个 ClassicalCondition 节点构造新的量子程序节点。

参数:

cc (ClassicalCondition) -- 要转换为量子程序的 ClassicalCondition 节点。

返回:

一个新的量子程序节点。

__init__(node_iter: NodeIter)

使用一个 NodeIter 节点构造新的量子程序节点。

参数:

node_iter (NodeIter) -- 要转换为量子程序的 NodeIter 节点。

返回:

一个新的量子程序节点。

get_max_qubit_addr()

获取量子程序中最大的量子比特地址，下标从0开始

get_qgate_num()

获取量子程序中的量子门数量。

get_used_cbits(cbit_vector: List[ClassicalCondition]) → List[ClassicalCondition]

获取量子程序中使用的经典比特列表。

参数:

cbit_vector (List[ClassicalCondition]) -- 用于存储使用的经典比特的列表。

返回:

使用的经典比特列表。

返回类型:

List[ClassicalCondition]

get_used_qubits(qubit_vector: QVec) → QVec

获取量子程序中使用的量子比特列表。

参数:

qubit_vector (QVec) -- 用于存储使用的量子比特的列表。

返回:

使用的量子比特列表。

返回类型:

QVec

insert(node: QProg | QGate | QCircuit | QIfProg | QWhileProg | QMeasure | QReset | ClassicalCondition) → QProg

在量子程序中插入一个节点。

参数:

node (Union[QProg, QGate, QCircuit, QIfProg, QWhileProg, QMeasure, QReset, ClassicalCondition]) -- 要插入的节点。

返回:

修改后的量子程序。

返回类型:

QProg

is_empty()

判断量子程序是否为空。

is_measure_last_pos()

判断量子程序最后一个节点是否为测量操作。

last()

获取量子程序的最后一个节点。

__lshift__(node: QProg | QGate | QCircuit | QIfProg | QWhileProg | QMeasure | QReset | ClassicalCondition) → QProg

通过左移操作符在量子程序中插入一个节点。

参数:

node (Union[QProg, QGate, QCircuit, QIfProg, QWhileProg, QMeasure, QReset, ClassicalCondition]) -- 要插入的节点。

返回:

修改后的量子程序。

返回类型:

QProg

它也是QNode中的一种，初始化一个QProg对象也可以使用下面的方式

prog = create_empty_qprog()

还可以由已有的QNode节点来构建量子程序，如：

qubit = qAlloc()

gate = H(qubit)

prog = QProg(gate)

可以用类似的方式构建量子程序的有QCircuit、QGate、QWhileProg、QIfProg、ClassicalCondition、QMeasure。

你可以通过如下方式向QProg尾部填充节点, 在这里pyqpanda重载了 << 运算符作为插入量子线路的方法

prog << node

QNode的类型有QGate，QPorg，QIf，Measure等等，QProg支持插入所有类型的QNode

QProg还支持 cast_qprog_qcircuit 接口，可以将QProg转换成QCircuit类型：

cir = cast_qprog_qcircuit(prog)
print(cir)

QProg还支持 cast_qprog_qgate 接口，可以将QProg转换成QGate类型：

gate = cast_qprog_qgate(prog)

QProg还支持 cast_qprog_qmeasure 接口，可以将QProg转换成QMeasure类型：

qmeas = cast_qprog_qmeasure(prog)

---

from pyqpanda import *

if __name__ == "__main__":

    qvm = CPUQVM()
    qvm.init_qvm()
    qubits = qvm.qAlloc_many(4)
    cbits = qvm.cAlloc_many(4)
    prog = QProg()

    # 构建量子程序
    prog << H(qubits[0]) \
         << X(qubits[1]) \
         << iSWAP(qubits[0], qubits[1]) \
         << CNOT(qubits[1], qubits[2]) \
         << H(qubits[3]) \
         << measure_all(qubits, cbits)

    # 量子程序运行1000次，并返回测量结果
    result = qvm.run_with_configuration(prog, cbits, 1000)

    # 打印量子态在量子程序多次运行结果中出现的次数
    print(result)

运行结果：

{'0001': 232, '0111': 263, '1001': 243, '1111': 262}

QProg支持 get_all_used_qubits 接口，可以获取到QProg中所有已使用到的比特信息：

used_qv = get_all_used_qubits(prog)

量子测量

量子测量是量子力学中的基本概念之一，用于引入外界的干扰获取量子系统的信息。在量子计算中，量子测量是评估量子比特状态的一种方式，它对量子信息的提取和观测起着至关重要的作用。

在量子计算中，测量通常被建模为对量子比特的一种操作，该操作将一个或多个量子比特的状态映射到经典的位（0或1）上。测量的结果是随机的，遵循一定的概率分布，这与量子力学的本质相关。

测量操作可以通过一系列测量门来实现，这些门用于将量子比特状态映射到经典位。蒙特卡洛方法在量子测量中的应用是指使用随机数模拟量子测量的随机性。在蒙特卡洛方法中，我们可以随机生成一组数值，这些数值代表测量结果的概率分布。通过模拟大量的测量，我们可以得到相应的统计数据，从而逼近真实的量子测量结果。

需要注意的是，量子测量会破坏量子系统的纯态，使其坍缩到一个确定的经典状态上。这个过程被称为量子态的“坍缩”或“投影”，而坍缩后的状态是测量结果所对应的状态。

在量子线路中用如下图标表示：

接口介绍

本章主要介绍获得量子测量对象、根据配置运行含有量子测量的量子程序、快速测量。

在量子程序中我们需要对某个量子比特做测量操作，并把测量结果存储到经典寄存器上，可以通过下面的方式获得一个测量对象：

Measure(qubit: Qubit | int, cbit: ClassicalCondition | CBit) → QMeasure

此函数用于创建一个量子测量节点，用于测量给定的量子比特，并将测量结果存储在指定的经典比特中。

参数:

• qubit (Union[Qubit, int]) -- 要测量的量子比特。可以是量子比特对象或量子比特的索引。

• cbit (Union[ClassicalCondition, CBit]) -- 存储量子测量结果的经典比特。可以是经典比特对象或经典比特的索引。

返回:

一个量子测量节点，表示测量操作。

返回类型:

QMeasure

如果想测量所有的量子比特并将其存储到对应的经典寄存器上，可以使用 measure_all ：

measure_all(qubit_list: QVec | List[int], cbit_list: List[ClassicalCondition]) → QProg

创建一组量子测量节点

此函数用于创建一组量子测量节点，用于同时测量给定的多个量子比特，并将测量结果分别存储在对应的经典比特中。

param qubit_list:

要测量的量子比特列表。可以是量子比特对象列表或量子比特的索引列表。

type qubit_list:

Union[QVec, List[int]]

param cbit_list:

存储量子测量结果的经典比特列表。

type cbit_list:

List[ClassicalCondition]

return:

一个量子程序，包含一组量子测量节点，表示同时对多个量子比特进行测量。

rtype:

QProg

备注

measure_all 的返回值类型是 QProg。

在得到含有量子测量的程序后，我们可以调用 directly_run 或 run_with_configuration 来得到量子程序的测量结果。

1. 直接运行量子程序并返回运行的结果 ：directly_run

directly_run(self, qprog: QProg, noise_model: Noise = NoiseModel()) → Dict[str, bool]

该方法用于直接运行量子程序，无需预先初始化。在使用此方法之前，请确保已进行初始化（init）操作。

参数:

• qprog (QProg) -- 要运行的量子程序。

• noise_model (Noise, optional) -- 噪声模型，默认为无噪声模型。噪声模型目前仅在 CPUQVM 上生效。

返回:

量子程序执行结果的字典，包含两个键值对。第一个键为最终量子比特寄存器状态，第二个键为其测量概率。

返回类型:

Dict[str, bool]

示例用法:

from pyqpanda import *
qvm = CPUQVM()
qvm.init_qvm()
qubits = qvm.qAlloc_many(4)
cbits = qvm.cAlloc_many(4)

prog = QProg()
prog << H(qubits[0])\
     << CNOT(qubits[0], qubits[1])\
     << CNOT(qubits[1], qubits[2])\
     << CNOT(qubits[2], qubits[3])\
     << Measure(qubits[0], cbits[0])

result = qvm.directly_run(prog)

2. 统计量子程序多次运行的测量结果 : run_with_configuration

run_with_configuration(self, qprog: QProg, cbit_list: List[ClassicalCondition] | List[int], data: dict, noise_model: Noise = NoiseModel()) → Dict[str, int]

此函数用于以配置信息运行量子程序，并返回在不同运行次数下的执行结果。

参数:

• qprog (QProg) -- 要运行的量子程序。

• cbit_list (Union[List[ClassicalCondition], List[int]]) -- 存储测量结果的经典比特列表或经典比特索引列表。

• data (dict) -- 配置信息，用于不同运行次数的设置。

• noise_model (Noise, optional) -- 噪声模型，用于模拟噪声影响。默认为无噪声模型。

返回:

在不同运行次数下的执行结果。结果以字典形式返回，键为量子态的二进制字符串表示，值为对应的命中次数。

返回类型:

Dict[str, int]

run_with_configuration(self, qprog: QProg, shot: int, noise_model: Noise = NoiseModel()) → Dict[str, int]

此函数用于以配置信息运行量子程序，并返回在指定运行次数下的执行结果。

参数:

• qprog (QProg) -- 要运行的量子程序。

• shot (int) -- 运行次数。

• noise_model (Noise, optional) -- 噪声模型，用于模拟噪声影响。默认为无噪声模型。

返回:

在指定运行次数下的执行结果。结果以字典形式返回，键为量子态的二进制字符串表示，值为对应的命中次数。

返回类型:

Dict[str, int]

示例用法:

from pyqpanda import *

machine = CPUQVM()
machine.init_qvm()

qubits = machine.qAlloc_many(3)
cbits = machine.cAlloc_many(3)

prog = QProg()
prog << H(qubits[0])\
     << H(qubits[0])\
     << H(qubits[1])\
     << H(qubits[2])\
     << measure_all(qubits, cbits)
result = run_with_configuration(prog, 1000)

实例

from pyqpanda import *

if __name__ == "__main__":
    qvm = CPUQVM()
    qvm.init_qvm()
    qubits = qvm.qAlloc_many(4)
    cbits = qvm.cAlloc_many(4)

    # 构建量子程序
    prog = QProg()
    prog << H(qubits[0])\
         << H(qubits[1])\
         << H(qubits[2])\
         << H(qubits[3])\
         << measure_all(qubits, cbits)

    # 量子程序运行1000次，并返回测量结果
    result = qvm.run_with_configuration(prog, cbits, 1000)

    # 打印测量结果
    print(result)

运行结果：

{'0000': 59, '0001': 69, '0010': 52, '0011': 62,
'0100': 63, '0101': 67, '0110': 79, '0111': 47,
'1000': 73, '1001': 59, '1010': 72, '1011': 60,
'1100': 61, '1101': 71, '1110': 50, '1111': 56}

3. 获取哈密顿期望 : get_expectation

   哈密顿期望是指系统处于某个量子态时，哈密顿算符在该量子态下的平均值。它描述了系统在该量子态下的平均能量。哈密顿期望的数学表达式为：

   ⟨H⟩ψ=⟨ψ|H|ψ⟩

   其中，⟨ψ| 是波函数的共轭，H 是哈密顿算符，|ψ⟩ 是波函数。这个期望值可以通过对哈密顿算符和波函数进行内积运算来求得。

get_expectation(self: pyqpanda.pyQPanda.QuantumMachine, qprog: pyqpanda.pyQPanda.QProg, hamiltonian: List[Tuple[Dict[int, str], float]], qubit_list: pyqpanda.pyQPanda.QVec) → float

此函数用于在虚拟机中获取哈密顿期望

参数:

• self (pyqpanda.pyQPanda.QuantumMachine) -- QuantumMachine，get_expectation是其成员函数

• qprog (QProg) -- 要运行的量子程序。

• hamiltonian -- 选择的哈密顿。

• qubit_list (pyqpanda.pyQPanda.QVec) -- 要测量的qubit的列表。

返回:

哈密顿期望的值

返回类型:

float

示例

from pyqpanda import *

# 构建泡利算符
# 参考： 8.Operators/index.html
p = PauliOperator({"Z0":2})
# 获得哈密顿量
Hmt = p.to_hamiltonian(False)
# 申请量子计算资源
qvm= init_quantum_machine(QMachineType.CPU)
# 申请量子比特，用于执行线路
qvec = qvm.qAlloc_many(1)
prog = QProg()
prog << H(qvec[0])
# 获取哈密顿期望
expec =qvm.get_expectation(prog,Hmt,QVec(qvec))
# 打印哈密顿期望
print(expec)

执行结果

0.0

get_expectation(self: pyqpanda.pyQPanda.QuantumMachine, qprog: pyqpanda.pyQPanda.QProg, hamiltonian: List[Tuple[Dict[int, str], float]], qubit_list: pyqpanda.pyQPanda.QVec, shots: int) → float

此函数用于在虚拟机中获取哈密顿期望

参数:

• self (pyqpanda.pyQPanda.QuantumMachine) -- QuantumMachine，get_expectation是其成员函数

• qprog (QProg) -- 要运行的量子程序。

• hamiltonian -- 选择的哈密顿。

• qubit_list (pyqpanda.pyQPanda.QVec) -- 要测量的qubit的列表。

• shots (int) -- measure shots

返回:

哈密顿期望的值

返回类型:

float

示例

from pyqpanda import *

# 构建泡利算符
# 参考： 8.Operators/index.html
p = PauliOperator({"Z0":2})
# 获得哈密顿量
Hmt = p.to_hamiltonian(False)
# 申请量子计算资源
qvm= init_quantum_machine(QMachineType.CPU)
# 申请量子比特，用于执行线路
qvec = qvm.qAlloc_many(1)
prog = QProg()
prog << H(qvec[0])
# 获取哈密顿期望
expec =qvm.get_expectation(prog,Hmt,QVec(qvec),100)
# 打印哈密顿期望
print(expec)

执行结果

0.0

get_expectation(self, prog: QProg, hamiltonian: List[Tuple[Dict[int, str], float]], qvec: QVec, task_name: str = 'QPanda Experiment')

此函数用于在云平台中获取哈密顿期望

参数:

• self (QCloud) -- QCloud，get_expectation是其成员函数

• qprog (QProg) -- 要运行的量子程序。

• hamiltonian -- 选择的哈密顿。

• qubit_list (pyqpanda.pyQPanda.QVec) -- 要测量的qubit的列表。

• task_name (str) -- 提交至云平台的任务的名称

示例

from pyqpanda import *

from pyqpanda import *
import numpy as np

# 通过QCloud()创建量子云虚拟机
QCM = QCloud()

# 通过传入当前用户的token来初始化
QCM.init_qvm("用户自己的token",True)

# 构建泡利算符
# 参考： 8.Operators/index.html

# 2倍的"泡利Z0"张乘"泡利Z1" + 3倍的"泡利X1"张乘"泡利Y2"
p = PauliOperator({"Z0":2})
# 获得哈密顿量
Hmt = p.to_hamiltonian(False)
qvec = QCM.qAlloc_many(1)
prog = QProg()
prog << H(qvec[0])

expec =QCM.get_expectation(prog,Hmt,[0])
# 打印哈密顿期望
print(expec)

执行结果

0.0

QIf

QIf表示量子程序条件判断操作，输入参数为条件判断表达式，功能是执行条件判断。

在量子计算中，除了对量子比特进行操作外，还可以根据经典寄存器的状态来执行条件操作。这意味着我们可以根据经典寄存器中存储的经典信息来决定是否执行特定的量子操作。

这种条件操作使得量子计算能够根据经典信息灵活地调整量子门的应用，从而实现更加复杂和多样化的计算过程。

例如，假设我们有一个经典寄存器中存储了一个位的值，可以是0或1。我们可以根据这个位的值来决定是否对量子比特应用某个特定的量子门操作。如果经典寄存器中的位是0，我们执行一系列操作；如果位是1，我们执行另一系列操作。通过这种方式，我们可以在量子计算中引入经典信息，从而实现更加智能和可控的计算过程。

在量子计算中，经典寄存器是与量子比特（qubit）相对应的一个概念。

由于量子计算和经典计算是不同的计算模型，它们之间需要有适当的接口来实现数据的传递和交互。经典寄存器就是这种接口之一，用于在量子计算和经典计算之间传递信息。

经典寄存器是一个类似于经典计算机中的比特（bit）的概念，它代表了一个经典的二进制值（0或1）。

在量子计算中，经典寄存器用于记录量子计算的结果。当量子计算完成后，量子比特的测量结果将被存储在经典寄存器中，以供后续的经典计算和分析使用。

在一些量子计算算法和量子门操作中，可能需要基于经典信息来控制量子操作，即 QIf、QWhile 操作等，经典寄存器可以用于记录这些控制信息，从而实现更复杂的量子计算任务。

class ClassicalCondition

经典寄存器类

__init__(*args, **kwargs)

初始化 ClassicalCondition 类实例。

get_val() → int

获取经典条件的值。

返回:

经典条件的值。

返回类型:

int

set_val(value: int) → None

设置经典条件的值。

参数:

value (int) -- 要设置的经典条件的值。

返回:

无返回值。

__add__(other: ClassicalCondition | int) → ClassicalCondition

重载操作符 +，用于经典条件的加法运算。

参数:

other (Union[ClassicalCondition, int]) -- 要进行加法运算的另一个经典条件或整数。

返回:

计算结果作为新的经典条件。

返回类型:

ClassicalCondition

__eq__(other: ClassicalCondition | int) → ClassicalCondition

重载操作符 ==，用于经典条件的等于比较。

参数:

other (Union[ClassicalCondition, int]) -- 要进行等于比较的另一个经典条件或整数。

返回:

计算结果作为新的经典条件。

返回类型:

ClassicalCondition

__ge__(other: ClassicalCondition | int) → ClassicalCondition

重载操作符 >=，用于经典条件的大于等于比较。

参数:

other (Union[ClassicalCondition, int]) -- 要进行大于等于比较的另一个经典条件或整数。

返回:

计算结果作为新的经典条件。

返回类型:

ClassicalCondition

__gt__(other: ClassicalCondition | int) → ClassicalCondition

重载操作符 >，用于经典条件的大于比较。

参数:

other (Union[ClassicalCondition, int]) -- 要进行大于比较的另一个经典条件或整数。

返回:

计算结果作为新的经典条件。

返回类型:

ClassicalCondition

__le__(other: ClassicalCondition | int) → ClassicalCondition

重载操作符 <=，用于经典条件的小于等于比较。

参数:

other (Union[ClassicalCondition, int]) -- 要进行小于等于比较的另一个经典条件或整数。

返回:

计算结果作为新的经典条件。

返回类型:

ClassicalCondition

__lt__(other: ClassicalCondition | int) → ClassicalCondition

重载操作符 <，用于经典条件的小于比较。

参数:

other (Union[ClassicalCondition, int]) -- 要进行小于比较的另一个经典条件或整数。

返回:

计算结果作为新的经典条件。

返回类型:

ClassicalCondition

__mul__(other: ClassicalCondition | int) → ClassicalCondition

重载操作符 *，用于经典条件的乘法运算。

参数:

other (Union[ClassicalCondition, int]) -- 要进行乘法运算的另一个经典条件或整数。

返回:

计算结果作为新的经典条件。

返回类型:

ClassicalCondition

__radd__(other: int) → ClassicalCondition

重载操作符 +，用于右侧加法运算。

参数:

other (int) -- 要进行加法运算的整数。

返回:

计算结果作为新的经典条件。

返回类型:

ClassicalCondition

__rmul__(other: int) → ClassicalCondition

重载操作符 *，用于右侧乘法运算。

参数:

other (int) -- 要进行乘法运算的整数。

返回:

计算结果作为新的经典条件。

返回类型:

ClassicalCondition

__rsub__(other: int) → ClassicalCondition

重载操作符 -，用于右侧减法运算。

参数:

other (int) -- 要进行减法运算的整数。

返回:

计算结果作为新的经典条件。

返回类型:

ClassicalCondition

__rtruediv__(other: int) → ClassicalCondition

重载操作符 /，用于右侧除法运算。

参数:

other (int) -- 要进行除法运算的整数。

返回:

计算结果作为新的经典条件。

返回类型:

ClassicalCondition

__sub__(other: ClassicalCondition | int) → ClassicalCondition

重载操作符 -，用于经典条件的减法运算。

参数:

other (Union[ClassicalCondition, int]) -- 要进行减法运算的另一个经典条件或整数。

返回:

计算结果作为新的经典条件。

返回类型:

ClassicalCondition

__truediv__(other: ClassicalCondition | int) → ClassicalCondition

重载操作符 /，用于经典条件的除法运算。

参数:

other (Union[ClassicalCondition, int]) -- 要进行除法运算的另一个经典条件或整数。

返回:

计算结果作为新的经典条件

c_and(arg0: ClassicalCondition | int) → ClassicalCondition

执行与其他经典条件或整数的逻辑与操作。

参数:

arg0 (Union[ClassicalCondition, int]) -- 用于逻辑与操作的其他经典条件或整数。

返回:

作为新的经典条件的与操作结果。

返回类型:

ClassicalCondition

c_not() → ClassicalCondition

执行逻辑非操作。

返回:

作为新的经典条件的非操作结果。

返回类型:

ClassicalCondition

c_or(arg0: ClassicalCondition | int) → ClassicalCondition

执行与其他经典条件或整数的逻辑或操作。

参数:

arg0 (Union[ClassicalCondition, int]) -- 用于逻辑或操作的其他经典条件或整数。

返回:

作为新的经典条件的或操作结果。

返回类型:

ClassicalCondition

在QPanda2中，QIfProg类用于表示执行量子程序条件判断操作，它也是QNode中的一种，QIf的定义如下：

class QIfProg

表示量子条件分支的类，有两种初始化方式。

__init__(self, arg0: NodeIter) → None

创建一个量子条件分支节点。

参数:

arg0 (NodeIter) -- 分支节点的迭代器。

返回:

无返回值

返回类型:

None

创建一个具有指定迭代器的量子条件分支节点。

__init__(self, classical_cond: ClassicalCondition, true_branch_qprog: QProg) → None

创建一个量子条件分支节点，具有一个正确分支的情况。

参数:

• classical_cond (ClassicalCondition) -- 用于判断是否执行正确分支的经典条件。

• true_branch_qprog (QProg) -- 正确分支的量子线路。

返回:

无返回值

返回类型:

None

创建一个具有给定经典条件和正确分支量子线路的量子条件分支节点。

__init__(self, classical_cond: ClassicalCondition, true_branch_qprog: QProg, false_branch_qprog: QProg) → None

创建一个量子条件分支节点，具有正确分支和错误分支的情况。

参数:

• classical_cond (ClassicalCondition) -- 用于判断是否执行正确分支的经典条件。

• true_branch_qprog (QProg) -- 正确分支的量子线路。

• false_branch_qprog (QProg) -- 错误分支的量子线路。

返回:

无返回值

返回类型:

None

创建一个具有给定经典条件、正确分支量子线路和错误分支量子线路的量子QIf节点。

get_classical_condition(self) → ClassicalCondition

获取该量子条件分支节点的经典条件。

返回:

经典条件

返回类型:

ClassicalCondition

get_false_branch(self) → QProg

获取该量子条件分支节点的错误分支量子线路。

返回:

错误分支量子线路

返回类型:

QProg

get_true_branch(self) → QProg

获取该量子条件分支节点的正确分支量子线路。

返回:

正确分支量子线路

返回类型:

QProg

可以传入的QNode类型有： QProg、QCircuit、QGate、QWhileProg、QIfProg、QMeasure。

from pyqpanda import *

if __name__ == "__main__":

    qvm = CPUQVM()
    qvm.init_qvm()
    qubits = qvm.qAlloc_many(3)
    cbits = qvm.cAlloc_many(3)
    cbits[0].set_val(0)
    cbits[1].set_val(3)

    prog = QProg()
    branch_true = QProg()
    branch_false = QProg()

    # 构建QIf正确分支以及错误分支
    branch_true << H(qubits[0])<< H(qubits[1]) << H(qubits[2])
    branch_false << H(qubits[0]) << CNOT(qubits[0], qubits[1]) << CNOT(qubits[1], qubits[2])

    # 构建QIf
    qif = QIfProg(cbits[0] > cbits[1], branch_true, branch_false)

    # QIf插入到量子程序中
    prog << qif

    # 概率测量，并返回目标量子比特的概率测量结果，下标为十进制
    result = qvm.prob_run_tuple_list(prog, qubits, -1)

    # 打印概率测量结果
    print(result)

运行结果：

[(0, 0.4999999999999999), (7, 0.4999999999999999), (1, 0.0), (2, 0.0), (3, 0.0), (4, 0.0), (5, 0.0), (6, 0.0)]

经典寄存器可以同时实现一些经典的判断表达式或者逻辑语句，例如经典逻辑中的and和or，代码示例如下：

from pyqpanda import *
import binascii

if __name__ == "__main__":
    qvm = CPUQVM();
    qvm.init_qvm();
    qubits = qvm.qAlloc_many(3);
    cbits = qvm.cAlloc_many(6);

    test_prog = QProg();
    test_prog << H(qubits[0]) \
        << CNOT(qubits[0], qubits[1]) \
        << H(qubits[2]) \
        << Measure(qubits[0], cbits[0])\
        << Measure(qubits[1], cbits[1])\
        << Measure(qubits[2], cbits[2]) \
        << Measure(qubits[0], cbits[3])\
        << Measure(qubits[1], cbits[4])\
        << Measure(qubits[2], cbits[5])

    result_test = qvm.run_with_configuration(test_prog, cbits, 1000);
    print(result_test)

    p = QProg();
    p << H(qubits[0]) \
        << CNOT(qubits[0], qubits[1]) \
        << H(qubits[2]) \
        << Measure(qubits[0], cbits[0])\
        << Measure(qubits[1], cbits[1])\
        << Measure(qubits[2], cbits[2])

    true_prog1 = QProg();
    true_prog2 = QProg();
    true_prog3 = QProg();
    true_prog4 = QProg();

    true_prog3 << X(qubits[2]);

    if_prog3 = create_if_prog((cbits[0] == 0).c_and(cbits[1] == 0).c_and(cbits[2] == 0), true_prog3)

    p << if_prog3
    p << Measure(qubits[0], cbits[3])\
        << Measure(qubits[1], cbits[4])\
        << Measure(qubits[2], cbits[5])

    result = qvm.run_with_configuration(p, cbits, 1000)
    print(result)

运行结果：

{'000000': 257, '011011': 259, '100100': 237, '111111': 247}
{'011011': 251, '100000': 220, '100100': 263, '111111': 266}

QWhile

---

无论是经典计算还是量子计算领域中，循环结构在许多算法和应用中扮演着重要角色。

量子QWhile循环节点是一种在量子程序中实现循环结构的机制，使得我们能够基于经典条件来重复执行一系列量子操作。这一概念类似于传统编程语言中的while循环，但在量子计算中涉及了量子比特和量子门操作。

实现量子While循环的常见方法是通过一个经典控制条件来判断循环是否继续，当然也可以是量子经典寄存器，一个典型的使用案例是利用量子QWhile循环节点来实现迭代优化算法，在这种情况下，经典条件可以是一组优化参数的变化是否达到收敛，而循环体中的量子操作可以是执行某种量子优化步骤。通过不断重复这个循环，我们可以逐步优化量子态或量子门操作，以实现更精确的结果。

在QPanda2中，QWhileProg类用于表示执行量子程序while循环操作，它也是QNode中的一种，QWhileProg的定义如下：

class QWhileProg

量子 While 循环节点用于在量子程序中实现循环结构，允许基于经典条件重复执行量子操作。

__init__(self, arg0: NodeIter) → None

创建一个 Quantum While 循环节点。

参数:

arg0 (NodeIter) -- 循环中的量子操作的迭代器。

返回:

无返回值

返回类型:

None

该构造函数创建一个 Quantum While 循环节点，其中循环体是由迭代器中的量子操作构成。在每次循环迭代中，将执行迭代器中的量子操作。

__init__(self, arg0: ClassicalCondition, arg1: QProg) → None

创建一个 Quantum While 循环节点。

参数:

• arg0 (ClassicalCondition) -- 控制循环执行的经典条件。

• arg1 (QProg) -- 循环体中的量子操作。

返回:

无返回值

返回类型:

None

该构造函数创建一个 Quantum While 循环节点，其中循环体是由参数中的量子操作构成。循环将根据经典条件判断是否继续执行循环体中的操作。

get_classical_condition(self) → ClassicalCondition

获取循环的经典条件。

返回:

循环的经典条件。

返回类型:

ClassicalCondition

该方法返回用于控制循环执行的经典条件，该条件将在每次循环迭代前进行判断。

get_true_branch(self) → QProg

获取循环体中的量子操作。

返回:

循环体中的量子操作。

返回类型:

QProg

该方法返回在循环体中定义的量子操作，这些操作将在每次循环迭代中执行。

可以传入的QNode类型有： QProg、QCircuit、QGate、QWhileProg、QIfProg、QMeasure。

关于经典寄存器可以参考 经典寄存器 。

from pyqpanda import *

if __name__ == "__main__":

    qvm = CPUQVM()
    qvm.init_qvm()
    qubits = qvm.qAlloc_many(3)
    cbits = qvm.cAlloc_many(3)
    cbits[0].set_val(0)
    cbits[1].set_val(1)

    prog = QProg()
    prog_while = QProg()

    # 构建QWhile的循环分支
    prog_while << H(qubits[0]) << H(qubits[1])<< H(qubits[2])\
            << assign(cbits[0], cbits[0] + 1) << Measure(qubits[1], cbits[1])

    # 构建QWhile
    qwhile = QWhileProg(cbits[1], prog_while)

    # QWhile插入到量子程序中
    prog << qwhile

    # 运行，并打印测量结果
    result = qvm.directly_run(prog)
    print(result)
    print(cbits[0].get_val())

运行结果：

{'c1': False}
0

量子程序统计

量子程序统计

在量子算法的设计以及量子计算机的性能分析中，经常需要对外界计算参数——量子程序进行分析，了解量子程序的结构信息对于优化和调试量子算法至关重要。

为了帮助研究者和开发者更方便地获取量子程序的结构信息，我们提供了一个便捷的接口 count_prog_info ，用于统计量子程序的节点数和层数

通过使用这个接口，可以快速了解量子程序的总节点数、总层数以及各类型节点和层的数量，为进一步的研究和优化提供有力支持，以及同时提供简单的可视化接口

当涉及到量子程序的层数（Layer）时，我们实际上在描述量子门（Quantum Gate）的分层排列方式。层数是用来表示量子程序中各个量子门在时间轴上的位置关系，从而更好地理解量子计算过程的组织和流程。

在量子计算中，每一层代表了一组同时执行的量子门操作，这些操作可以并行地在量子计算机的不同量子比特上进行。在某一层内，所有的量子门操作都是同时发生的，而不同层之间的操作可以顺序执行。通过合理地分层和排列，我们可以最大限度地利用量子计算机的并行性，提高量子算法的效率。

考虑下面的例子：

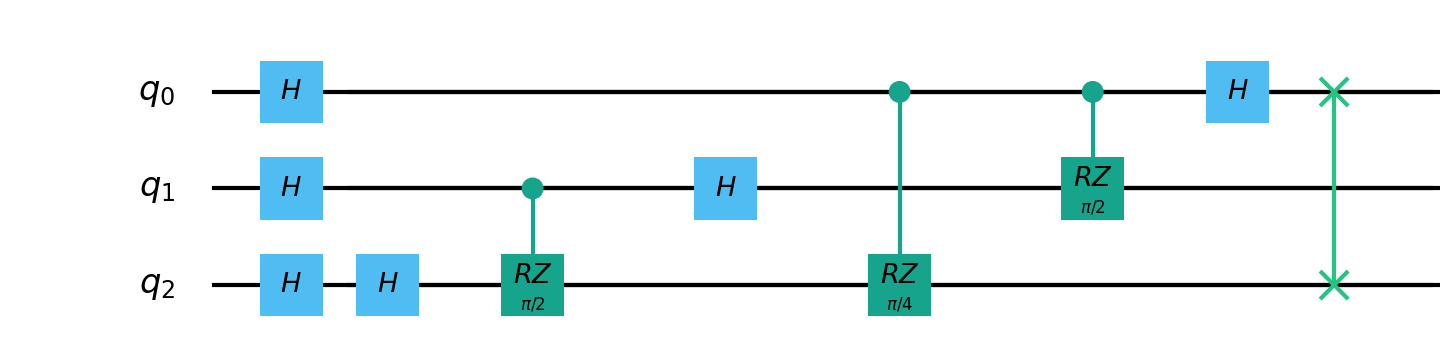
在这个例子中，第一层的三个H门可以同时执行，上图中一共可以划分为7层，我们可以采用不同的优化策略和编译算法来最小化层数，从而优化量子程序的执行效率和减少量子比特的错误率。

总之，量子程序的层数是对量子门操作在时间上排列的一种描述，用于指导量子计算的顺序执行。理解层数的概念对于优化和调试量子程序非常重要。

pyqpanda中可以使用 count_prog_info 对层数和节点数进行统计。

class ProgCount

该类用于统计量子程序的信息，包括双比特门层数、双比特门数量、单比特门数量、多控制门数量、总量子门数量、层数、节点数量等。

double_gate_layer_num

纯双比特门的层数。

double_gate_num

双比特门的数量。

gate_num

总门的数量。

layer_num

量子线路的层数。

node_num

节点的数量。

single_gate_layer_num

纯单比特门的层数。

single_gate_num

单比特门的数量。

multi_control_gate_num

多控制门的数量。

selected_gate_nums

选取特定量子门的数量

__init__()

初始化 ProgCount 类实例。

count_prog_info(node: QProg, select_gate_types: [] = None) → ProgCount

该函数用于统计给定量子程序的信息，包括门层数、门数量等。

参数:

node (QProg or QCircuit) -- 要统计信息的量子程序。

返回:

ProgCount 结构，包含统计信息。

返回类型:

ProgCount

注意：函数支持两种重载方式，分别接受 QProg 和 QCircuit 类型的量子程序作为参数，可以选择指定要统计的量子逻辑门数量合集

示例用法:

# 统计 QProg 的信息
prog_info = count_prog_info(my_qprog)

# 统计 QCircuit 的信息，并启用优化
optimized_info = count_prog_info(my_qcircuit ,[pq.GateType.HADAMARD_GATE])

# 获取统计结果的各种属性
num_layers = prog_info.layer_num
num_gates = prog_info.gate_num
num_double_gates = prog_info.double_gate_num
# ... 其他属性获取

具体示例可参考下面的程序：

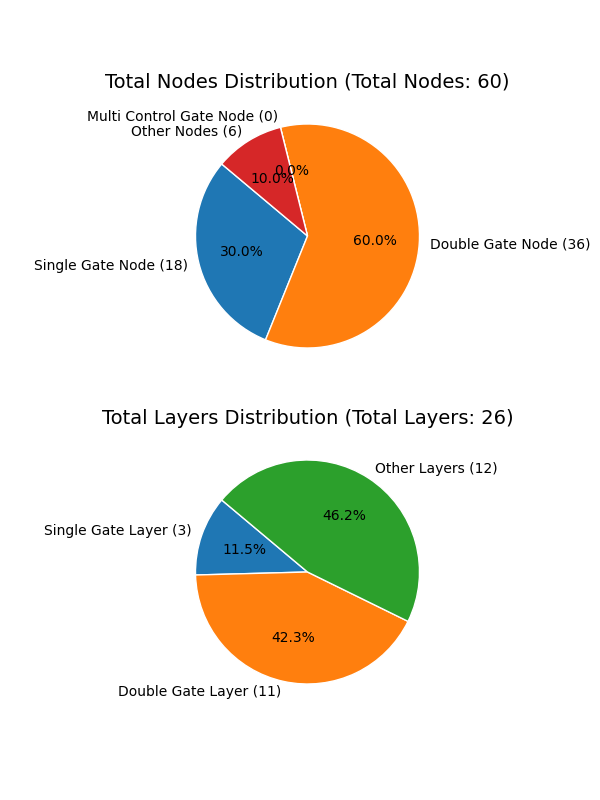
import pyqpanda as pq
import matplotlib.pyplot as plt

machine = pq.CPUQVM()
machine.init_qvm()

q = machine.qAlloc_many(6)
c = machine.cAlloc_many(6)

prog = pq.QProg()
prog << pq.hadamard_circuit(q) << pq.QFT(q) << pq.QFT(q) << pq.measure_all(q,c)

prog_info = pq.count_prog_info(prog,[pq.GateType.HADAMARD_GATE])

#总节点数，包括逻辑门，测量和reset等
print("all nodes num : ",prog_info.node_num)

#总逻辑门数量
print("all gate num : ",prog_info.gate_num)

#总层数
print("all layer num : ",prog_info.layer_num)

#总的单门数量
print("single gate num : ",prog_info.single_gate_num)

#总的双门数量
print("double gate num : ",prog_info.double_gate_num)

#纯单门构成的层数
print("single gate layer num : ",prog_info.single_gate_layer_num)

#纯双门构成的层数
print("double gate layer num : ",prog_info.double_gate_layer_num)

#筛选的量子逻辑门数量
print("selected_gate_nums : ",prog_info.selected_gate_nums)

#可视化接口
pq.show_prog_info_count(prog)

运行结果如下：

all nodes num :  60
all gate num :  54
all layer num :  26
single gate num :  18
double gate num :  36
single gate layer num :  3
double gate layer num :  11
selected_gate_nums :  {<GateType.HADAMARD_GATE: 10>: 18}

量子程序时钟周期

量子程序时钟周期用于在已知每个量子逻辑门在运行时所需时间的条件下，估算一个量子程序运行所需要的时间。

每个量子逻辑门的时间设置在项目的元数据配置文件 QPandaConfig.xml 中， 如果未设置则会给定一个默认值，单量子门的默认时间为1，双量子门的时间为2。

"QGate": {
    "SingleGate":{
        "U3":{"time":1}
    },
    "DoubleGate":{
        "CNOT":{"time":2},
        "CZ":{"time":2}
    }
}

具体时间根据每一层中运行时间最长的量子操作依次累加得到的时间，以下图为例，我们可以一共划分为 4 层

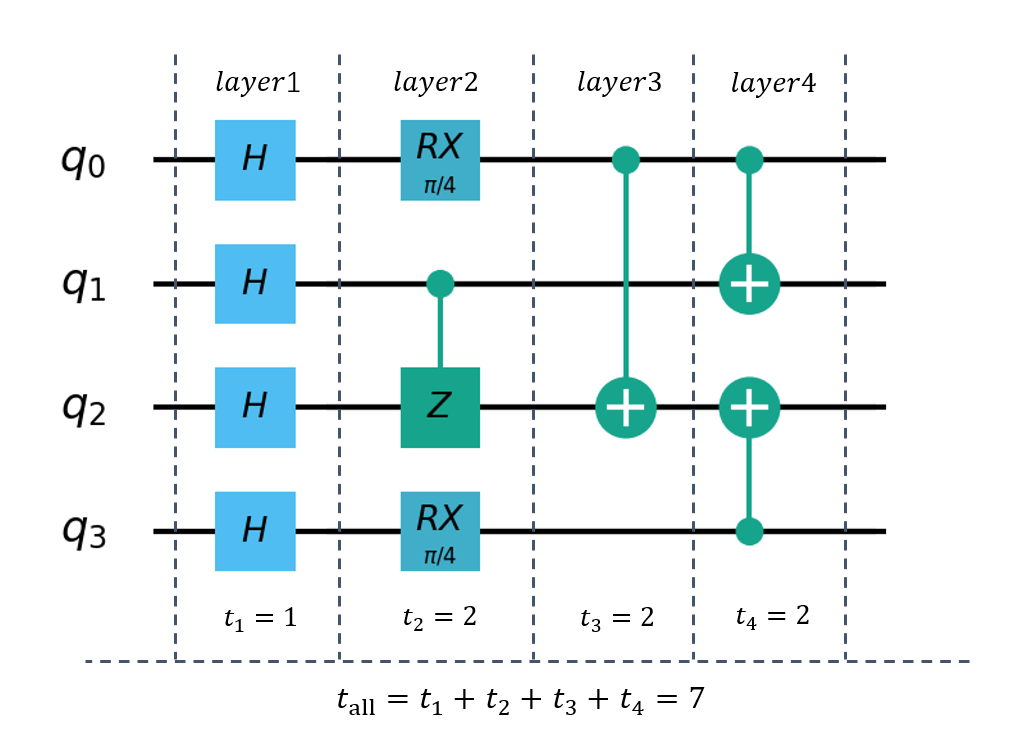
最终的时钟周期数为每一层的时间累加。

接口介绍

get_qprog_clock_cycle(qprog: QProg, machine: QuantumMachine, optimize: bool = False) → int

该函数用于计算给定量子程序在指定量子机器上运行所需的时钟周期数，可以选择是否进行优化来获取不同条件下的时钟周期数。

参数:

• qprog (QProg) -- 要计算时钟周期的量子程序。

• machine (QuantumMachine) -- 执行量子程序的量子机器。

• optimize (bool, optional) -- 是否对量子程序进行优化。默认为 False，为True时需要提供配置文件

返回:

量子程序运行所需的时钟周期数，没有单位，不以秒为单位。

返回类型:

int

示例用法:

cycle_count = get_qprog_clock_cycle(my_qprog, my_machine, optimize=True)

备注

时钟周期数是一个与具体硬件和实现有关的相对量，不具备实际物理单位。

参见

QProg, QuantumMachine

我们先用pyQPanda构建一个量子程序：

prog = QProg()
prog << H(qubits[0]) << CNOT(qubits[0], qubits[1])\
     << iSWAP(qubits[1], qubits[2]) << RX(qubits[3], np.pi / 4)

然后调用 get_qprog_clock_cycle 接口得到量子程序的时钟周期

clock_cycle = get_qprog_clock_cycle(prog, qvm)

实例

from pyqpanda import *
import numpy as np

if __name__ == "__main__":
    qvm = CPUQVM()
    qvm.init_qvm()
    qubits = qvm.qAlloc_many(4)
    cbits = qvm.cAlloc_many(4)

    # 构建量子程序
    prog = QProg()
    prog << H(qubits[0]) << CNOT(qubits[0], qubits[1])\
         << iSWAP(qubits[1], qubits[2]) << RX(qubits[3], np.pi / 4)

    # 统计量子程序时钟周期
    clock_cycle = get_qprog_clock_cycle(prog, qvm)

    print(clock_cycle)

运行结果：

5