量子态编码

简介

量子态编码是一个将经典信息转化为量子态的过程。在使用量子算法解决经典问题的过程中，量子态编码是非常重要的一步。比如在使用HHL算法解如下线性方程组时

\[\begin{split}\begin{aligned} A=\left(\begin{array}{cc} 1 & -1 / 3 \\ -1 / 3 & 1 \end{array}\right), \vec{x}=\left(\begin{array}{l} x_{1} \\ x_{2} \end{array}\right), \vec{b}=\left(\begin{array}{l} 1 \\ 0 \end{array}\right) \end{aligned}\end{split}\]

需要将向量b编码至线路中。而大多数量子态编码都是以 \(\left|0\right\rangle\) 为基态进行制备，而制备后的经典信息则可以表现在量子线路的各个参数中。本教程中我们将讨论四种量子编码的方式，包括基态编码、角度编码、振幅编码、IQP 编码。在pyqpanda中，我们内置了这四类量子编码方式至 Encode 类中。

class Encode: Encode类提供了多种量子态编码方法，用于将量子态编码为不同格式的函数，其中包括编码为二进制串的基态编码，编码至角度及相位的角度编码，以及针对稀疏数据、密集数据的多种振幅编码方式，以及近似振幅编码方法。

基态编码

basic_encode(qubit, data)

基态编码[1]是将一个 \(n\) 位的二进制字符串 \(x\) 转换为一个具有 \(n\) 个量子比特的系统的量子态 \(\left|x\right\rangle=\left|\psi\right\rangle\) 其中， \(\left|\psi\right\rangle\) 为转换后的计算基态。例如，当需要对一个长度为4的二进制字符串 \(1001\) 编码时，得到的结果即为 \(\left|1001\right\rangle\) 。

参数:

qubit (QVec) -- 编码比特列表。
data (str) -- 编码数据。

返回:

None

返回类型:

None

示例:

from pyqpanda import *
import numpy as np

if __name__=="__main__":

    #构建全振幅虚拟机
    qvm = CPUQVM()
    qvm.init_qvm()

    x = '1001'

    #申请量子比特
    qubits = qvm.qAlloc_many(4)

    #实例化编码类Encode
    cir_encode=Encode()

    #调用Encode类中基态编码接口
    cir_encode.basic_encode(qubits,x)

    #调用Encode类中内置获取编码线路接口
    prog = QProg()
    prog << cir_encode.get_circuit()

    #获取量子编码后的编码比特
    encode_qubits = cir_encode.get_out_qubits()

    #获取线路的概率测量结果
    result = qvm.prob_run_dict(prog, encode_qubits)

    print(result)

{'0000': 0.0, '0001': 0.0, '0010': 0.0, '0011': 0.0, '0100': 0.0, '0101': 0.0, '0110': 0.0, '0111': 0.0, '1000': 0.0, '1001': 1.0, '1010': 0.0, '1011': 0.0, '1100': 0.0, '1101': 0.0, '1110': 0.0, '1111': 0.0}

角度编码

angle_encode(qubit, data, gate_type = GateType::RY_GATE)
角度编码[1]即是利用旋转门 \(R_{x}\) , \(R_{y}\) , \(R_{z}\) 的旋转角度进行对经典信息的编码。

\[\begin{aligned} |\boldsymbol{x}\rangle=\bigotimes_{i=1}^{N} \cos \left(x_{i}\right)|0\rangle+\sin \left(x_{i}\right)|1\rangle \end{aligned}\]

其中 \(\left|x\right\rangle\) 即为所需编码的经典数据向量。

参数:

qubit (QVec) -- 编码比特列表。

data (List[float]) -- 编码数据。

Parm gate_type:

编码的泡利旋转门类型，默认为 RY_GATE

返回:

None

返回类型:

None

示例:

下面我们以 \(R_{y}\) 门编码一组角度 \([\pi,\pi]\) 为例
from pyqpanda import *
import numpy as np

if __name__=="__main__":

    #构建全振幅虚拟机
    qvm = CPUQVM()
    qvm.init_qvm()
    x = [np.pi,np.pi]

    #申请量子比特
    qubits = qvm.qAlloc_many(2)

    #实例化编码类Encode
    cir_encode = Encode()

    #调用Encode类中经典角度编码或密集角度编码接口并输出概率
    cir_encode.angle_encode(qubits,x)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits=cir_encode.get_out_qubits()
    result = qvm.prob_run_dict(prog, encode_qubits)
    print(result)
    qvm.finalize()
{'00': 1.405799628556214e-65, '01': 3.749399456654644e-33, '10': 3.749399456654644e-33, '11': 1.0}
dense_angle_encode(qubit, data)
由于一个qubit不仅可以加载角度信息，还可以加载相位信息，因此，我们完全可以将一个长度为N的经典数据编码至 \(\lceil N \rceil\) 个量子比特上。

\[\begin{aligned} |\boldsymbol{x}\rangle=\bigotimes_{i=1}^{\lceil N / 2\rceil} \cos \left(\pi x_{2 i-1}\right)|0\rangle+e^{2 \pi i x_{2 i}} \sin \left(\pi x_{2 i-1}\right)|1\rangle \end{aligned}\]

其中，将两个数据分别编码至量子特的旋转角度 \(\cos \left(\pi x_{2 i-1}\right)|0\rangle\) 与相位信息中 \(e^{2 \pi i x_{2 i}} \sin \left(\pi x_{2 i-1}\right)|1\rangle\)。

参数:

qubit (QVec) -- 编码比特列表。

data (List[float]) -- 编码数据。

返回:

None

返回类型:

None

可以发现，在经典角度编码中将经典数据向量 \(x\) 向 \(y\) 轴旋转了 \(\pi\)。由于密集角度编码会将一半信息编码至量子态的相位信息中。那么，我们可以调用 pyqpanda 的 qvm.directly_run 接口，获取系统的量子态信息，
from pyqpanda import *
import numpy as np

if __name__=="__main__":

    #构建全振幅虚拟机
    qvm = CPUQVM()
    qvm.init_qvm()
    x = [np.pi,np.pi]
    x = np.asarray(x)
    #实例化编码类Encode
    cir_encode = Encode()

    #申请量子比特
    qubits = qvm.qAlloc_many(1)
    cir_encode.dense_angle_encode(qubits,x)
    prog = QProg()
    prog << cir_encode.get_circuit()
    qvm.directly_run(prog)
    result = qvm.get_qstate()
    print(result)
    qvm.finalize()
[(6.123233995736766e-17+0j), (-1+1.2246467991473532e-16j)]

振幅编码

振幅编码即是将一个长度为 \(N\) 的数据向量 \(x\) 编码至数量为 \(\lceil log_{2}N \rceil\) 的量子比特的振幅上，具体公式如下：

\[\begin{aligned} \left|\psi\right\rangle=x_{0}|0\rangle+\cdots+x_{N-1}|N-1\rangle \end{aligned}\]

然而，可以发现由于处于纯态或混合态的量子系统的迹是为1的，所以我们需要将数据进行归一化处理，因此在接口入参时会进行校验。同时，一个编码算法需要考虑的通常有三点，分别为编码线路的深度，宽度(qubit数量)，以及CNOT门的数量。因此，对应以上三点，在pyqpanda中也提供了不同的编码方法。同时根据数据形式的不同也可分为密集数据编码和稀疏数据编码。

amplitude_encode(qubit, data)

Top-down[2]的编码方式，顾名思义，即是将数据向量先进行处理，得到对应的角度树，并从角度树的根节点开始，依次向下进行编码，如下图所示：

参数:

qubit (QVec) -- 编码比特列表。
data (List[float] 或 List[complex]) -- 编码数据。

返回:

None

返回类型:

None

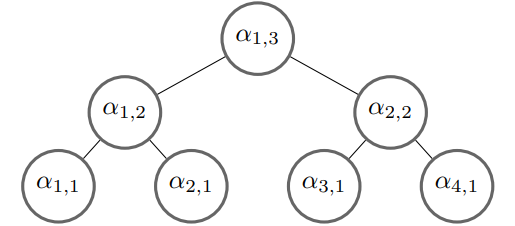
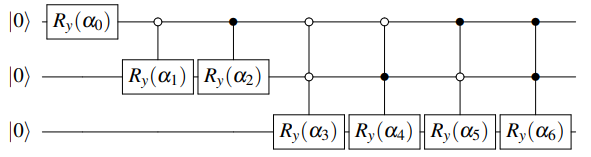
这种编码方式具有 \(O(\lceil log_{2} N \rceil)\) 的线路宽度，以及 \(O(n)\) 的线路深度。

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine=CPUQVM()
    machine.init_qvm()

    data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
    data = np.asarray(data)
    qubit = machine.qAlloc_many(3)
    cir_encode = Encode()
    cir_encode.amplitude_encode(qubit,data)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

                                                               ┌────────────┐     ┌────────────┐     >
q_0:  |0>─────────────── ────────────── ─── ────────────── ─── ┤RY(0.000000)├ ─── ┤RY(3.141593)├ ─── >
                         ┌────────────┐     ┌────────────┐     └──────┬─────┘ ┌─┐ └──────┬─────┘ ┌─┐ >
q_1:  |0>─────────────── ┤RY(1.570796)├ ─── ┤RY(0.000000)├ ─── ───────■────── ┤X├ ───────■────── ┤X├ >
          ┌────────────┐ └──────┬─────┘ ┌─┐ └──────┬─────┘ ┌─┐        │       └─┘        │       ├─┤ >
q_2:  |0>─┤RY(1.910633)├ ───────■────── ┤X├ ───────■────── ┤X├ ───────■────── ─── ───────■────── ┤X├ >
          └────────────┘                └─┘                └─┘                                   └─┘ >

         ┌────────────┐     ┌────────────┐
q_0:  |0>┤RY(0.000000)├ ─── ┤RY(3.141593)├ ───
         └──────┬─────┘ ┌─┐ └──────┬─────┘ ┌─┐
q_1:  |0>───────■────── ┤X├ ───────■────── ┤X├
                │       └─┘        │       ├─┤
q_2:  |0>───────■────── ─── ───────■────── ┤X├
                                           └─┘

{'000': 1.2497998188848808e-33, '001': 0.33333333333333315, '010': 0.0, '011': 0.0, '100': 1.2497998188848817e-33, '101': 0.3333333333333334, '110': 0.3333333333333334, '111': 0.0}

dc_amplitude_encode(qubit, data)

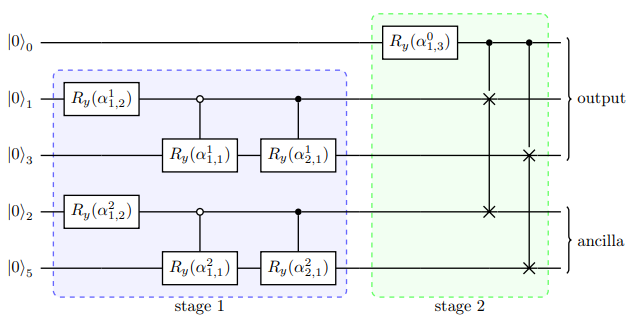
与Top-down编码方式相反，Bottom-top[2]通过 \(O(n)\) 的宽度构建一个 \(O(\lceil log_{2} N \rceil)\) 深度的量子线路。其中，角度树中最左子树( \(\alpha_{0}\) , \(\alpha_{1}\) , \(\alpha_{3}\) )对应的量子比特为输出比特，其余为辅助比特。构建形式如下图所示：

参数:

qubit (QVec) -- 编码比特列表。
data (List[float]) -- 编码数据。

返回:

None

返回类型:

None

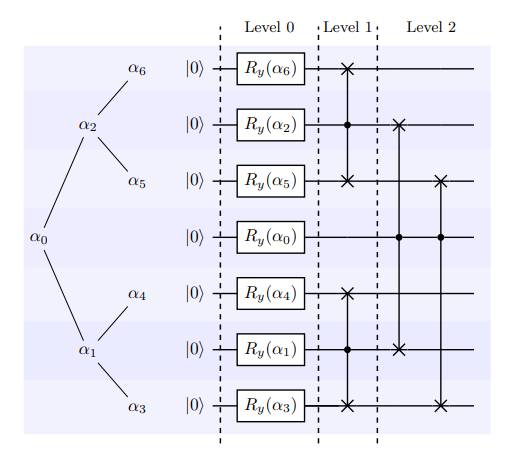
其中，level1，与level2对应的量子逻辑门为受控SWAP门，其作用为交换辅助比特与输出比特量子态。

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine = CPUQVM()
    machine.init_qvm()

    data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
    data = np.asarray(data)
    qubit = machine.qAlloc_many(7)
    cir_encode = Encode()
    cir_encode.dc_amplitude_encode(qubit,data)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

          ┌────────────┐
q_0:  |0>─┤RY(1.910633)├ ─── ■─ ■─
          ├────────────┤     │  │
q_1:  |0>─┤RY(0.000000)├ ■── X─ ┼─
          ├────────────┤ │   │  │
q_2:  |0>─┤RY(1.570796)├ ┼■─ X─ ┼─
          ├────────────┤ ││     │
q_3:  |0>─┤RY(3.141593)├ X┼─ ── X─
          ├────────────┤ ││     │
q_4:  |0>─┤RY(0.000000)├ X┼─ ── ┼─
          ├────────────┤  │     │
q_5:  |0>─┤RY(3.141593)├ ─X─ ── X─
          ├────────────┤  │
q_6:  |0>─┤RY(0.000000)├ ─X─ ── ──
          └────────────┘


{'000': 1.2497998188848807e-33, '001': 0.33333333333333315, '010': 0.0, '011': 0.0, '100': 1.2497998188848817e-33, '101': 0.3333333333333334, '110': 0.3333333333333334, '111': 0.0}

bid_amplitude_encode(qubit, data, spilt)

双向振幅编码[2]则是综合了Top-down和Bottom-top两种编码方式，即可通过参数 \(split\) 控制决定其线路深度与宽度。其线路宽度为 \(O_{w}\left(2^{split}+\log _{2}^{2}(N)-split^{2}\right)\) ，线路深度为 \(O_{d}\left((split+1) \frac{N}{2^{split}}\right)\) ，而在我们pyqpanda中的接口默认为 \(n/2\)。从 \(O_{w}\) 和 \(O_{d}\) 的公式可以看出当split为1时，则为Bottom-top振幅编码，当spilt为n时则为Top-down振幅编码。

参数:

qubit (QVec) -- 编码比特列表。
data (List[float]) -- 编码数据。
spilt (int) -- 量子线路深度与宽度调节因子，其宽度表达式为 \(O_{w}\left(2^{split}+\log _{2}^{2}(N)-split^{2}\right)\) ，深度表达式为 \(O_{d}\left((split+1) \frac{N}{2^{split}}\right)\)，默认值为 \(N/2\)

返回:

None

返回类型:

None

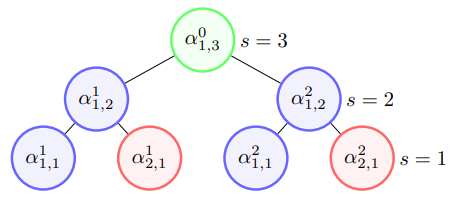
from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine=CPUQVM()
    machine.init_qvm()

    data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
    qubit = machine.qAlloc_many(5)
    data = np.asarray(data)
    cir_encode = Encode()
    cir_encode.bid_amplitude_encode(qubit,data)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

          ┌────────────┐
q_0:  |0>─┤RY(1.910633)├ ────────────── ─── ────────────── ─── ■─ ■─
          ├────────────┤                ┌─┐                ┌─┐ │  │
q_1:  |0>─┤RY(0.000000)├ ───────■────── ┤X├ ───────■────── ┤X├ X─ ┼─
          └────────────┘ ┌──────┴─────┐ └─┘ ┌──────┴─────┐ └─┘ │  │
q_2:  |0>─────────────── ┤RY(0.000000)├ ─── ┤RY(3.141593)├ ─── ┼─ X─
          ┌────────────┐ └────────────┘ ┌─┐ └────────────┘ ┌─┐ │  │
q_3:  |0>─┤RY(1.570796)├ ───────■────── ┤X├ ───────■────── ┤X├ X─ ┼─
          └────────────┘ ┌──────┴─────┐ └─┘ ┌──────┴─────┐ └─┘    │
q_4:  |0>─────────────── ┤RY(0.000000)├ ─── ┤RY(3.141593)├ ─── ── X─
                         └────────────┘     └────────────┘


{'000': 1.2497998188848807e-33, '001': 0.33333333333333315, '010': 0.0, '011': 0.0, '100': 1.2497998188848813e-33, '101': 0.3333333333333334, '110': 0.3333333333333334, '111': 0.0}

schmidt_encode(qubit, data, cutoff)

如Top-down振幅编码所示，使用 \(\lceil log_{2} N \rceil\) 个量子比特编码长度为：\(N\) 的经典数据大约需要 \(2^{2n}\) 个受控旋转门，这极大的降低了量子线路的保真度，然而基于schmidt分解振幅编码[3]可以有效降低线路中的受控旋转门数量。首先，一个纯态 \(|\psi\rangle\) 可以被表示为如下形式：

\[\begin{aligned} |\psi\rangle=\sum_{i=1}^{k} \lambda_{i}\left|\alpha_{i}\right\rangle \otimes\left|\beta_{i}\right\rangle \end{aligned}\]

进一步，可以表示为：

\[\begin{aligned} |\psi\rangle=\sum_{i=1}^{m} \sum_{j=1}^{n} C_{i j}\left|e_{i}\right\rangle \otimes\left|f_{j}\right\rangle \end{aligned}\]

其中，\(\left|e_{i}\right\rangle \in \mathbb{C}^{m},\left|f_{j}\right\rangle \in \mathbb{C}^{n}\)。而 \(C\) 可以进行奇异值分解(svd) \(C=U \Sigma V^{\dagger}\), 通过以上公式，我们可以得出 \(\sigma_{i i}=\lambda_{i}\) ， \(\left|\alpha_{i}\right\rangle=U\left|e_{i}\right\rangle\) ， \(\left|\beta_{i}\right\rangle=V^{\dagger}\left|f_{i}\right\rangle\), 其中，\(\sigma_{i i}\) 则是 \(C\) 的奇异值。线路图构建如下：

参数:

qubit (QVec) -- 编码比特列表。
data (List[float]) -- 编码数据。
cutoff (double) -- 表示奇异值向量的截断系数，范围为[0,1)，0表示不截断。

返回:

None

返回类型:

None

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine=CPUQVM()
    machine.init_qvm()

    data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
    data = np.asarray(data)
    qubit = machine.qAlloc_many(3)
    cir_encode = Encode()
    cir_encode.schmidt_encode(qubit,data,0)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

                         ┌────┐              ┌────────────┐  ┌─────────────┐ ┌─────────────┐ ┌────────────┐ >
q_0:  |0>─────────────── ┤CNOT├───────────── ┤RZ(3.141593)├─ ┤RY(-2.588018)├ ┤RZ(-3.141593)├ ┤RX(1.570796)├ >
          ┌────────────┐ └──┬┬┴────────────┐ ├────────────┤  └─────────────┘ └─────────────┘ └────────────┘ >
q_1:  |0>─┤RZ(4.712389)├ ───┼┤RY(-1.570796)├ ┤RZ(1.570796)├─ ─────────────── ─────────────── ────────────── >
          ├────────────┤    │└─────────────┘ ├────────────┴┐ ┌─────────────┐                                >
q_2:  |0>─┤RY(0.729728)├ ───■─────────────── ┤RY(-2.034444)├ ┤RZ(-3.141593)├ ─────────────── ────────────── >
          └────────────┘                     └─────────────┘ └─────────────┘                                >

                ┌─────────────┐        ┌─────────────┐ ┌─────────────┐ ┌─────────────┐ ┌────────────┐ ┌─────────────┐
q_0:  |0>───■── ┤RX(-1.570796)├ ───■── ┤RX(-1.570796)├ ┤RY(-1.570796)├ ┤RZ(-1.570796)├ ┤U1(4.712389)├ ┤RZ(-4.712389)├
         ┌──┴─┐ ├─────────────┤ ┌──┴─┐ ├─────────────┤ └─────────────┘ └─────────────┘ └────────────┘ └─────────────┘
q_1:  |0>┤CNOT├ ┤RY(-1.017222)├ ┤CNOT├ ┤RY(-3.141593)├ ─────────────── ─────────────── ────────────── ───────────────
         └────┘ └─────────────┘ └────┘ └─────────────┘
q_2:  |0>────── ─────────────── ────── ─────────────── ─────────────── ─────────────── ────────────── ───────────────



{'000': 1.4442161374080831e-64, '001': 0.3333333333333333, '010': 3.8518598887744744e-32, '011': 1.2497998188848808e-33, '100': 1.2497998188848825e-33, '101': 0.3333333333333337, '110': 0.3333333333333337, '111': 1.2497998188848825e-33}

approx_mps(qubit, data, layers=3, sweeps=100, double2float=False)

MPS近似编码[4]是一种利用矩阵乘积态的低秩表达近似分布制备算法，可以通过一种较少的CNOT的门完成对分布的表达，并且这种表达是一种近邻接形式，因此可以直接作用于芯片，且双门个数的减少，也有利于增加分布制备的成功率，量子线路图如下所示。

参数:

qubit (QVec) -- 编码比特列表。
data (List[float] 或 List[complex]) -- 编码数据。
layers (int) -- 表示MPS解纠缠的所需的近似层数，一般来说，层数越多，近似度越高, 默认值为3。
sweep (int) -- 表示通过环境张量优化迭代次数，默认值为100。
double2float (bool) -- 表示将数据向量的类型从双精度变为单精度。

返回:

None

返回类型:

None

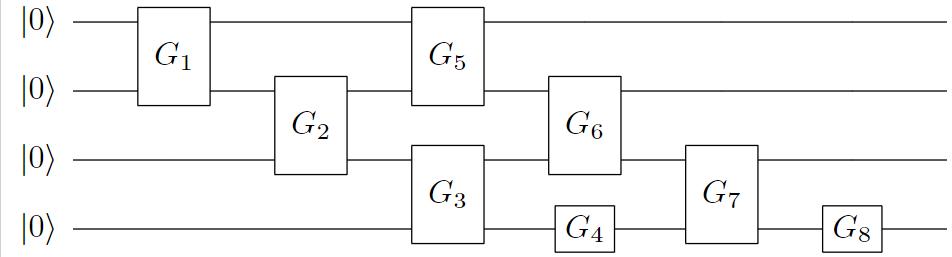
可以发现该函数支持多种类型数据制备（float，double，complex），其中layers指的是使用矩阵乘积态近似的层数，sweeps是指通过环境张量优化的迭代次数，double2float则是表示是否需要将双精度数据转为单精度类型处理，从而加速生成线路。环境张量的数学表达如下：

\[\begin{aligned} \hat{\mathcal{F}}_m=\operatorname{Tr}_{\bar{U}_m}\left[\prod_{i=M}^{m+1} U_i\left|\psi_{\chi_{\max }}\right\rangle\left\langle 0^{\otimes N}\right| \prod_{j=1}^{m-1} U_j^{\dagger}\right] \end{aligned}\]

其中， \(\operatorname{Tr}_{\bar{U}_m}\) 指的是不与 \(U_m\) 相互作用的量子比特索引上的偏迹，环境张量 \(\hat{\mathcal{F}}_m\) 则被表示为一个4x4的矩阵，在实际中可以通过从量子线路中移除 \(U_m\) 并收缩剩余的张量来计算(见下图)，并同时始终保持MPS结构。最后，为了适配芯片的拓扑结构，该制备算法的 \(chi\) 均为2。

下面，我们以W-state作为示例，展示MPS近似编码的神奇，即在无论多少比特的W-state，均可在一层解纠缠下完成准确编码。因此，针对纠缠度较低的数据，如正太分布数据，可在一个较低深度下近似表达。

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine = CPUQVM()
    machine.init_qvm()

    n_qubits = 5
    w_state = [0]*2**n_qubits
    for i in range(n_qubits):
        w_state[1<<i] = 1/np.sqrt(n_qubits)
    w_state = np.asarray(w_state)
    qubit = machine.qAlloc_many(n_qubits)
    cir_encode = Encode()
    cir_encode.approx_mps(qubit,data = w_state,layers=1)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

          ┌─────────────┐ ┌─────────────┐ ┌────────────┐ ┌────────────┐        ┌─────────────┐        >
q_0:  |0>─┤RZ(-1.570796)├ ┤RY(-1.570796)├ ┤RZ(4.712389)├ ┤RX(1.570796)├ ───■── ┤RX(-1.570796)├ ───■── >
          ├─────────────┤ ├────────────┬┘ └────────────┘ └────────────┘ ┌──┴─┐ ├─────────────┤ ┌──┴─┐ >
q_1:  |0>─┤RY(-0.463648)├ ┤RZ(3.141593)├─ ────────────── ────────────── ┤CNOT├ ┤RY(-1.107149)├ ┤CNOT├ >
          ├─────────────┤ ├────────────┴┐                               └────┘ └─────────────┘ └────┘ >
q_2:  |0>─┤RZ(-1.178097)├ ┤RZ(-1.178097)├ ────────────── ────────────── ────── ─────────────── ────── >
          ├────────────┬┘ ├─────────────┤                                                             >
q_3:  |0>─┤RZ(5.497787)├─ ┤RY(-1.570796)├ ────────────── ────────────── ────── ─────────────── ────── >
          ├────────────┴┐ ├─────────────┤                                                             >
q_4:  |0>─┤RZ(-1.963495)├ ┤RZ(-1.963495)├ ────────────── ────────────── ────── ─────────────── ────── >
          └─────────────┘ └─────────────┘                                                             >

         ┌─────────────┐ ┌────────────┐  ┌─────────────┐ ┌────────────┐                                       >
q_0:  |0>┤RX(-1.570796)├ ┤RZ(3.141593)├─ ┤U1(-4.712389)├ ┤RZ(4.712389)├ ────────────── ────── ─────────────── >
         ├─────────────┤ ├────────────┴┐ ├────────────┬┘ ├────────────┤ ┌────────────┐        ┌─────────────┐ >
q_1:  |0>┤RY(-1.570796)├ ┤RZ(-4.712389)├ ┤RZ(2.748894)├─ ┤RZ(2.748894)├ ┤RX(1.570796)├ ───■── ┤RX(-1.047198)├ >
         └─────────────┘ └─────────────┘ └────────────┘  └────────────┘ └────────────┘ ┌──┴─┐ ├─────────────┤ >
q_2:  |0>─────────────── ─────────────── ─────────────── ────────────── ────────────── ┤CNOT├ ┤RY(-1.047198)├ >
                                                                                       └────┘ └─────────────┘ >
q_3:  |0>─────────────── ─────────────── ─────────────── ────────────── ────────────── ────── ─────────────── >
                                                                                                              >
q_4:  |0>─────────────── ─────────────── ─────────────── ────────────── ────────────── ────── ─────────────── >
                                                                                                              >

                                                                                                      >
q_0:  |0>────── ─────────────── ─────────────── ─────────────── ─────────────── ────── ────────────── >
                ┌─────────────┐ ┌─────────────┐ ┌─────────────┐                                       >
q_1:  |0>───■── ┤RX(-1.570796)├ ┤RZ(-2.748894)├ ┤RZ(-2.748894)├ ─────────────── ────── ────────────── >
         ┌──┴─┐ ├────────────┬┘ ├────────────┬┘ ├────────────┬┘ ┌─────────────┐                       >
q_2:  |0>┤CNOT├ ┤RZ(1.178097)├─ ┤RZ(1.178097)├─ ┤RZ(3.926991)├─ ┤RY(-1.570796)├ ───■── ────────────── >
         └────┘ └────────────┘  └────────────┘  └────────────┘  └─────────────┘ ┌──┴─┐ ┌────────────┐ >
q_3:  |0>────── ─────────────── ─────────────── ─────────────── ─────────────── ┤CNOT├ ┤RZ(0.615480)├ >
                                                                                └────┘ └────────────┘ >
q_4:  |0>────── ─────────────── ─────────────── ─────────────── ─────────────── ────── ────────────── >
                                                                                                      >

                                                                                                     >
q_0:  |0>────────────── ────── ────────────── ────── ─────────────── ─────────────── ─────────────── >
                                                                                                     >
q_1:  |0>────────────── ────── ────────────── ────── ─────────────── ─────────────── ─────────────── >
                        ┌────┐ ┌────────────┐        ┌─────────────┐ ┌─────────────┐ ┌─────────────┐ >
q_2:  |0>────────────── ┤CNOT├ ┤RX(0.000000)├ ───■── ┤RX(-1.570796)├ ┤RZ(-3.141593)├ ┤RY(-1.570796)├ >
         ┌────────────┐ └──┬─┘ ├────────────┤ ┌──┴─┐ ├────────────┬┘ ├─────────────┤ ├─────────────┤ >
q_3:  |0>┤RX(1.570796)├ ───■── ┤RY(0.615480)├ ┤CNOT├ ┤RZ(3.141593)├─ ┤RY(-1.570796)├ ┤RZ(-0.785398)├ >
         └────────────┘        └────────────┘ └────┘ └────────────┘  └─────────────┘ └─────────────┘ >
q_4:  |0>────────────── ────── ────────────── ────── ─────────────── ─────────────── ─────────────── >
                                                                                                     >


q_0:  |0>─────────────── ─────────────── ────────────── ────── ─────────────── ────── ─────────────── ─────────────── ──────────────

q_1:  |0>─────────────── ─────────────── ────────────── ────── ─────────────── ────── ─────────────── ─────────────── ──────────────
         ┌─────────────┐ ┌─────────────┐ ┌────────────┐
q_2:  |0>┤RZ(-2.356194)├ ┤U1(-6.283185)├ ┤RZ(6.283185)├ ────── ─────────────── ────── ─────────────── ─────────────── ──────────────
         ├─────────────┤ ├─────────────┤ ├────────────┤        ┌─────────────┐        ┌─────────────┐ ┌────────────┐  ┌────────────┐
q_3:  |0>┤RZ(-2.748894)├ ┤RZ(-2.748894)├ ┤RX(1.570796)├ ───■── ┤RX(-0.785398)├ ───■── ┤RX(-1.570796)├ ┤RZ(1.178097)├─ ┤RZ(1.178097)├
         └─────────────┘ └─────────────┘ └────────────┘ ┌──┴─┐ ├─────────────┤ ┌──┴─┐ ├─────────────┤ ├────────────┴┐ └────────────┘
q_4:  |0>─────────────── ─────────────── ────────────── ┤CNOT├ ┤RY(-0.785398)├ ┤CNOT├ ┤RZ(-2.748894)├ ┤RZ(-2.748894)├ ──────────────
                                                        └────┘ └─────────────┘ └────┘ └─────────────┘ └─────────────┘


{'00000': 4.468157470978386e-32, '00001': 0.20000000000000048, '00010': 0.2000000000000004, '00011': 0.0, '00100': 0.20000000000000048, '00101': 7.4987989133093034e-34, '00110': 7.498798913309305e-34, '00111': 0.0, '01000': 0.20000000000000023, '01001': 1.4102295515520025e-35, '01010': 1.4102295515519843e-35, '01011': 0.0, '01100': 4.818833738106373e-33, '01101': 9.629649721936199e-35, '01110': 1.1555579666323412e-33, '01111': 0.0, '10000': 0.20000000000000023, '10001': 1.410229551551963e-35, '10010': 1.4102295515519827e-35, '10011': 0.0, '10100': 4.818833738106368e-33, '10101': 9.629649721936196e-35, '10110': 1.1555579666323415e-33, '10111': 0.0, '11000': 0.0, '11001': 3.851859888774471e-34, '11010': 0.0, '11011': 0.0, '11100': 3.851859888774471e-34, '11101': 5.934729841099873e-67, '11110': 0.0, '11111': 0.0}

ds_quantum_state_preparation(qubit, data)

双稀疏量子态编码[5]通过利用 \(n\) 个辅助比特辅助构建线路。我们以编码 \(|001\rangle\) 为例，如下图所示：

参数:

qubit (QVec) -- 编码比特列表。
data (List[float] 或 List[complex]) -- 编码数据。

返回:

None

返回类型:

None

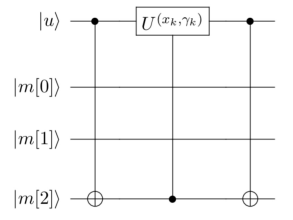
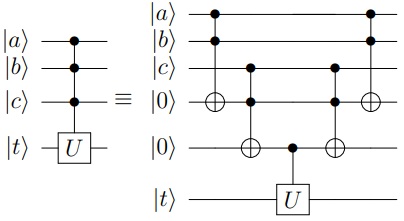
其中，\(|\mu\rangle\) 为辅助寄存器用以作用旋转门，并受输出寄存器 \(|m\rangle\) 控制，而当所需编码的字符下标的1的个数较多时，则需要作用多控门，而为了减少消除线路中多控门的数量，我们通过增加一部分辅助寄存器，并利用Toffoli门进行分解，其原理如下图所示：

../_images/double_sparse_decompostion.png

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine = CPUQVM()
    machine.init_qvm()
    data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
    data = np.asarray(data)
    qubit = machine.qAlloc_many(6)
    cir_encode = Encode()
    cir_encode.ds_quantum_state_preparation(qubit,data)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

          ┌─┐        ┌───────────────────────────────┐                          ┌───────────────────────────────┐ >
q_0:  |0>─┤X├ ───■── ┤U3(-1.230959,0.000000,0.000000)├ ───■── ───■── ───■── ─── ┤U3(-1.570796,0.000000,0.000000)├ >
          └─┘    │   └───────────────┬───────────────┘    │      │      │   ┌─┐ └───────────────┬───────────────┘ >
q_2:  |0>──── ───┼── ────────────────┼──────────────── ───┼── ───┼── ───┼── ┤X├ ────────────────■──────────────── >
              ┌──┴─┐                 │                 ┌──┴─┐ ┌──┴─┐    │   └┬┘                                   >
q_3:  |0>──── ┤CNOT├ ────────────────■──────────────── ┤CNOT├ ┤CNOT├ ───┼── ─■─ ───────────────────────────────── >
              └────┘                                   └────┘ └────┘    │    │                                    >
q_4:  |0>──── ────── ───────────────────────────────── ────── ────── ───┼── ─┼─ ───────────────────────────────── >
                                                                     ┌──┴─┐  │                                    >
q_5:  |0>──── ────── ───────────────────────────────── ────── ────── ┤CNOT├ ─■─ ───────────────────────────────── >
                                                                     └────┘                                       >

                                             ┌───────────────────────────────┐
q_0:  |0>─── ───■── ───■── ───■── ───■── ─── ┤U3(-3.141593,0.000000,0.000000)├ ───
         ┌─┐    │      │      │      │   ┌─┐ └───────────────┬───────────────┘ ┌─┐
q_2:  |0>┤X├ ───┼── ───┼── ───┼── ───┼── ┤X├ ────────────────■──────────────── ┤X├
         └┬┘ ┌──┴─┐    │      │      │   └┬┘                                   └┬┘
q_3:  |0>─■─ ┤CNOT├ ───┼── ───┼── ───┼── ─┼─ ───────────────────────────────── ─┼─
        │    └────┘    │   ┌──┴─┐    │    │                                     │
q_4:  |0>─┼─ ────── ───┼── ┤CNOT├ ───┼── ─■─ ───────────────────────────────── ─■─
        │           ┌──┴─┐ └────┘ ┌──┴─┐  │                                     │
q_5:  |0>─■─ ────── ┤CNOT├ ────── ┤CNOT├ ─■─ ───────────────────────────────── ─■─
                    └────┘        └────┘


{'000': 0.0, '001': 0.3333333333333333, '010': 0.0, '011': 0.0, '100': 0.0, '101': 0.3333333333333334, '110': 0.33333333333333315, '111': 0.0}

sparse_isometry(qubit, data)

sparse_isometry编码[6]不同于双稀疏量子态编码需要辅助比特去构建线路。 sparse_isometry编码首先通过将长度为 \(N\) 稀疏数据向量中的非0元素 \(x\) 统一编码至前 \(\lceil log_2len(x) \rceil\) 个量子比特上，后通过受控X门对其进行受控转化。其线路构建如下图所示：

参数:

qubit (QVec) -- 编码比特列表。
data (List[float] 或 List[complex]) -- 编码数据。

返回:

None

返回类型:

None

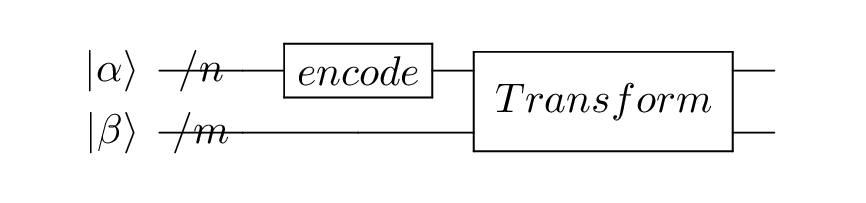
其中，\(n+m=\lceil log_2N \rceil\) \(|\alpha\rangle\) 为 \(\lceil log_2len(x) \rceil\) 个非0元素的编码encode模块，而 \(|\beta\rangle\) 则为剩余qubit。其中transform模块则是转化模块。

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine = CPUQVM()
    machine.init_qvm()
    data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
    data = np.asarray(data)
    qubit = machine.qAlloc_many(3)
    cir_encode = Encode()
    cir_encode.sparse_isometry(qubit,data)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

                         ┌────────────┐     ┌────────────┐ ┌─┐     ┌─┐ ┌─┐ ┌─┐     ┌─┐ ┌─┐
q_0:  |0>─────────────── ┤RY(0.000000)├ ─── ┤RY(1.570796)├ ┤X├ ─■─ ┤X├ ┤X├ ┤X├ ─■─ ┤X├ ┤X├
          ┌────────────┐ └──────┬─────┘ ┌─┐ └──────┬─────┘ ├─┤  │  ├─┤ └┬┘ └─┘  │  ├─┤ └┬┘
q_1:  |0>─┤RY(1.230959)├ ───────■────── ┤X├ ───────■────── ┤X├ ─■─ ┤X├ ─┼─ ─── ─■─ ┤X├ ─┼─
          └────────────┘                └─┘                └─┘ ┌┴┐ └─┘  │      ┌┴┐ └─┘  │
q_2:  |0>─────────────── ────────────── ─── ────────────── ─── ┤X├ ─── ─■─ ─── ┤X├ ─── ─■─
                                                               └─┘             └─┘


{'000': 0.0, '001': 0.3333333333333334, '010': 0.0, '011': 0.0, '100': 0.0, '101': 0.3333333333333333, '110': 0.3333333333333333, '111': 0.0}

efficient_sparse(qubit, data)

多项式稀疏量子态编码[7]是一种稀疏数据向量中的非0元素个数与qubit个数成线性关系的稀疏数据编码方式。其线路编码深度为 \(O\left(|S|^{2} \log (|S|) n\right)\) 。其中，\(|S|\) 为非0元素个数，\(n\) 为所需qubit个数，即为 \(\lceil log_2N \rceil\) , \(N\) 为稀疏数据长度。下面以编码 \(|x\rangle=1/\sqrt{3}(|001\rangle+|100\rangle+|111\rangle)\) 为例，其线路图构建如下：

参数:

qubit (QVec) -- 编码比特列表。
data (List[float] 或 List[complex]) -- 编码数据。

返回:

None

返回类型:

None

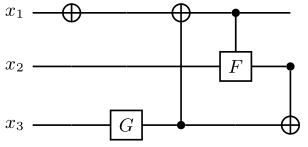
其中，F门是将 \(|0\rangle\) 映射到 \(1/\sqrt{3}|0\rangle+1/\sqrt{3}|1\rangle\) ，而G门则是将 \(|0\rangle\) 映射到 \(1/\sqrt{3}|0\rangle+2/\sqrt{3}|1\rangle\)。

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine = CPUQVM()
    machine.init_qvm()
    data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
    data = np.asarray(data)
    qubit = machine.qAlloc_many(3)
    cir_encode = Encode()
    cir_encode.efficient_sparse(qubit,data)
    prog = QProg()
    prog << cir_encode.get_circuit()
    encode_qubits = cir_encode.get_out_qubits()
    print(prog)
    result = machine.prob_run_dict(prog, encode_qubits)
    print(result)
    machine.finalize()

          ┌─┐                                      ┌────┐                                             >
q_0:  |0>─┤X├ ──────────────────────────────────── ┤CNOT├ ────── ──────────────────────────────────── >
          └─┘                                      └──┬─┘ ┌────┐                                      >
q_1:  |0>──── ──────────────────────────────────── ───┼── ┤CNOT├ ──────────────────■───────────────── >
          ┌─┐ ┌──────────────────────────────────┐    │   └──┬─┘ ┌─────────────────┴────────────────┐ >
q_2:  |0>─┤X├ ┤U3(1.230959,0.000000,0.000000).dag├ ───■── ───■── ┤U3(1.570796,0.000000,0.000000).dag├ >
          └─┘ └──────────────────────────────────┘               └──────────────────────────────────┘ >

         ┌────┐
q_0:  |0>┤CNOT├ ────── ───
         └──┬─┘ ┌────┐
q_1:  |0>───┼── ┤CNOT├ ───
            │   └──┬─┘ ┌─┐
q_2:  |0>───■── ───■── ┤X├
                       └─┘


{'000': 0.0, '001': 0.3333333333333333, '010': 0.0, '011': 0.0, '100': 0.0, '101': 0.3333333333333333, '110': 0.3333333333333334, '111': 0.0}

IQP编码

iqp_encode(qubit, data, control_vector=None, inverse=false, repeats=1)

IQP编码[8] iqp_encode(qubit, data, control_vector = None, inverse=false, repeats = 1) 是一种应用于量子机器学习的编码方法。将一个经典数据x编码到

\[\begin{aligned} |\mathbf{x}\rangle=\left(\mathrm{U}_{\mathrm{Z}}(\mathbf{x}) \mathrm{H}^{\otimes n}\right)^{\boldsymbol{r}}\left|0^{n}\right\rangle \end{aligned}\]

其中， \(r\) 表示量子线路的深度，也就是 \(\mathrm{U}_{\mathrm{Z}}(\mathbf{x}) \mathrm{H}^{\otimes n}\) 重复的次数。\(\mathrm{H}^{\otimes n}\) 是一层作用在所有量子比特上的Hadamard门。其中， \(\mathrm{U}_\mathrm{Z}\) 为

\[\begin{aligned} \mathrm{U}_\mathrm{Z}(\mathbf{x})=\prod_{[i, j] \in S} R_{Z_{i} Z_{j}}\left(x_{i} x_{j}\right) \bigotimes_{k=1}^{n} R_{z}\left(x_{k}\right) \end{aligned}\]

这里的 \(S\) 是一个集合，对于这个集合中的每一对量子比特，我们都需要对它们作用 \(R_{ZZ}\) 门。\(R_{ZZ}\) 门的构建形式如下：

参数:

qubit (QVec) -- 编码比特列表。
data (List[float]) -- 编码数据。
control_vector (List[tuple]) -- 控制序列，默认为空，则表示按序控制。
inverse (int) -- 是否翻转线路，默认为False。
inverse -- 表示重复模块次数，默认为1。

返回:

None

返回类型:

None

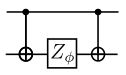
下面我们以编码 \(data=[-1.3, 1.8, 2.6, -0.15]\) 为例介绍：

from pyqpanda import *
import numpy as np

if __name__=="__main__":
    machine=CPUQVM()
    machine.init_qvm()

    data = [-1.3, 1.8, 2.6, -0.15]
    data = np.asarray(data)
    qubit = machine.qAlloc_many(4)
    cir_encode = Encode()
    cir_encode.iqp_encode(qubit,data)
    prog = QProg()
    prog << cir_encode.get_circuit()
    print(prog)
    encode_qubits = cir_encode.get_out_qubits()
    machine.directly_run(prog)
    result = machine.get_qstate()
    print(result)
    machine.finalize()

          ┌─┐ ┌─────────────┐
q_0:  |0>─┤H├ ┤RZ(-1.300000)├ ───■── ─────────────── ───■── ────── ────────────── ────── ────── ─────────────── ──────
          ├─┤ ├────────────┬┘ ┌──┴─┐ ┌─────────────┐ ┌──┴─┐
q_1:  |0>─┤H├ ┤RZ(1.800000)├─ ┤CNOT├ ┤RZ(-2.340000)├ ┤CNOT├ ───■── ────────────── ───■── ────── ─────────────── ──────
          ├─┤ ├────────────┤  └────┘ └─────────────┘ └────┘ ┌──┴─┐ ┌────────────┐ ┌──┴─┐
q_2:  |0>─┤H├ ┤RZ(2.600000)├─ ────── ─────────────── ────── ┤CNOT├ ┤RZ(4.680000)├ ┤CNOT├ ───■── ─────────────── ───■──
          ├─┤ ├────────────┴┐                               └────┘ └────────────┘ └────┘ ┌──┴─┐ ┌─────────────┐ ┌──┴─┐
q_3:  |0>─┤H├ ┤RZ(-0.150000)├ ────── ─────────────── ────── ────── ────────────── ────── ┤CNOT├ ┤RZ(-0.390000)├ ┤CNOT├
          └─┘ └─────────────┘                                                            └────┘ └─────────────┘ └────┘


[(-0.1925578135118269-0.15944117553362588j), (0.24534942018697528+0.047996479182488616j), (-0.02973039232415307+0.24822591277352968j), (-0.22912120333719244+0.10001736939810474j), (-0.06725827577934981-0.2407827326433292j), (0.17417667733679137+0.17933902272488078j), (0.1777283845030693-0.17581985480010265j), (0.2415974945336283+0.06427013797303885j), (-0.24713295520684903-0.037753178021585905j), (0.23511504508229614-0.08497597057962829j), (0.10212186022103938+0.22819098506513033j), (-0.14509671578880565+0.20358522310644894j), (-0.008095829439931083-0.249868880706821j), (0.1265550643081946+0.2156010568108347j), (0.21442717034095604-0.12853399791327838j), (0.21939564047259316+0.11985638465105079j)]

参考文献

[1] Schuld, Maria. "Quantum machine learning models are kernel methods."[J] arXiv:2101.11020 (2021).
[2] Araujo I F, Park D K, Ludermir T B, et al. "Configurable sublinear circuits for quantum state preparation."[J]. arXiv preprint arXiv:2108.10182, 2021.
[3] Ghosh K. "Encoding classical data into a quantum computer"[J]. arXiv preprint arXiv:2107.09155, 2021.
[4] Rudolph M S, Chen J, Miller J, et al. Decomposition of matrix product states into shallow quantum circuits[J]. arXiv preprint arXiv:2209.00595, 2022.
[5] de Veras T M L, da Silva L D, da Silva A J. "Double sparse quantum state preparation"[J]. arXiv preprint arXiv:2108.13527, 2021.
[6] Malvetti E, Iten R, Colbeck R. "Quantum circuits for sparse isometries"[J]. Quantum, 2021, 5: 412.
[7] N. Gleinig and T. Hoefler, "An Efficient Algorithm for Sparse Quantum State Preparation," 2021 58th ACM/IEEE Design Automation Conference (DAC), 2021, pp. 433-438, doi: 10.1109/DAC18074.2021.9586240.
[8] Havlíček, Vojtěch, et al. "Supervised learning with quantum-enhanced feature spaces." Nature 567.7747 (2019): 209-212.